كيفية التمهيد في لغة r (مع أمثلة)

Bootstrapping هي طريقة يمكن استخدامها لتقدير الخطأ المعياري لأي إحصائية وإنتاج فاصل ثقة للإحصاء.

العملية الأساسية للتمهيد هي كما يلي:

• خذ عينات متكررة مع الاستبدال من مجموعة بيانات معينة.
• لكل عينة، حساب الإحصائية للفائدة.
• وهذا يعطي k تقديرات مختلفة لإحصائية معينة، والتي يمكنك بعد ذلك استخدامها لحساب الخطأ المعياري للإحصاء وإنشاء فاصل ثقة للإحصاء.

يمكننا التمهيد في R باستخدام الوظائف التالية من مكتبة التمهيد :

1. إنشاء عينات تمهيدية.

التمهيد (البيانات، الإحصائيات، R، …)

ذهب:

• البيانات: ناقل أو مصفوفة أو كتلة من البيانات
• إحصائية: دالة تنتج الإحصائية (الإحصائيات) التي سيتم البدء فيها
• ج: عدد مرات تكرار التمهيد

2. قم بإنشاء فاصل ثقة للتمهيد.

boot.ci(كائن التمهيد، conf، النوع)

ذهب:

• bootobject: كائن تم إرجاعه بواسطة الدالة boot()
• conf: فاصل الثقة المطلوب حسابه. القيمة الافتراضية هي 0.95
• النوع: نوع فاصل الثقة المراد حسابه. تتضمن الخيارات “قياسي” و”أساسي” و”مسمار” و”perc” و”bca” و”all” – الافتراضي هو “all”

توضح الأمثلة التالية كيفية استخدام هذه الوظائف عمليًا.

المثال 1: تمهيد إحصائية واحدة

يوضح التعليمة البرمجية التالية كيفية حساب الخطأ القياسي لمربع R لنموذج الانحدار الخطي البسيط:

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

ومن النتائج يمكننا أن نرى:

• مربع R المقدر لنموذج الانحدار هذا هو 0.7183433 .
• الخطأ القياسي لهذا التقدير هو 0.06513426 .

يمكننا أيضًا تصور توزيع العينات التمهيدية بسرعة:

 plot(reps)

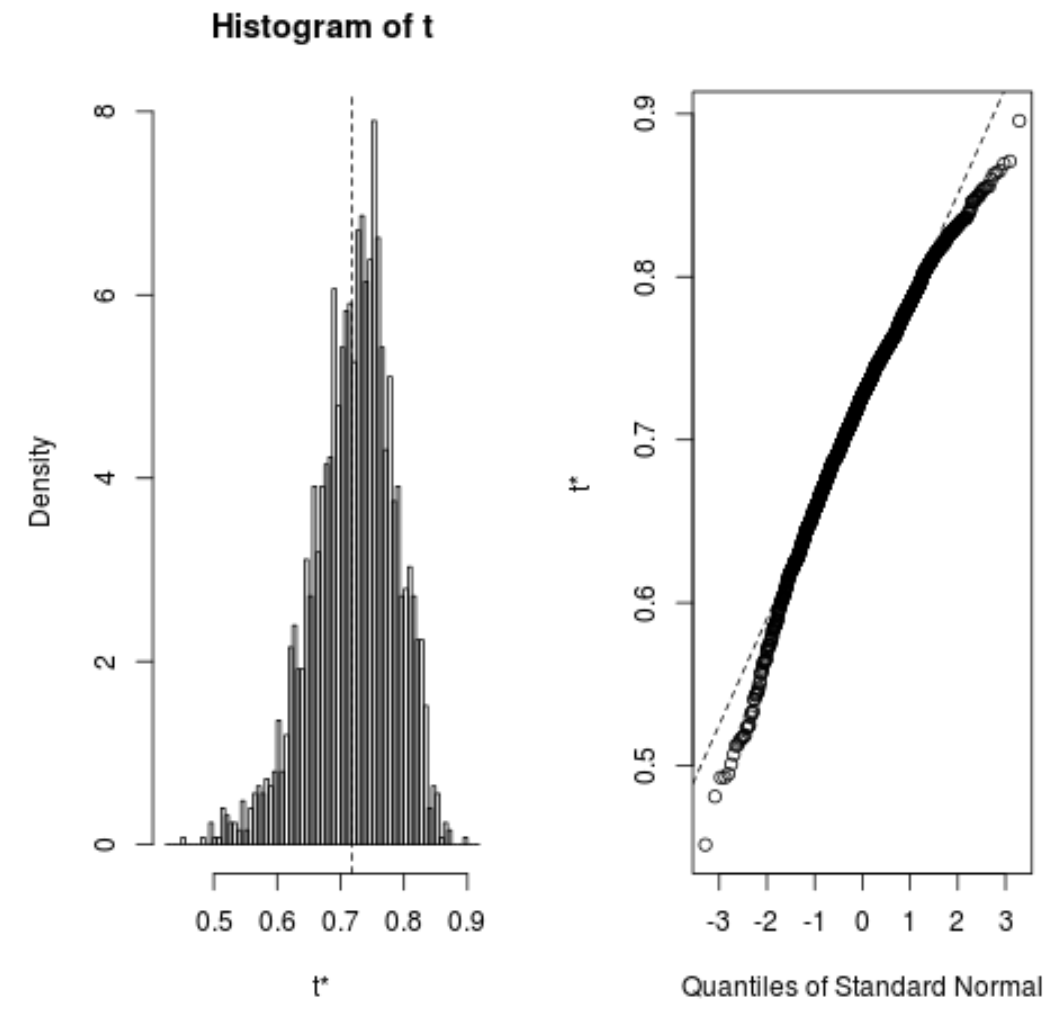
يمكننا أيضًا استخدام الكود التالي لحساب فاصل الثقة 95% لمربع R المقدر للنموذج:

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

من النتيجة يمكننا أن نرى أن فاصل الثقة 95٪ الذي تم تمهيده لقيم R-squared الحقيقية هو (0.5350، 0.8188).

مثال 2: تمهيد إحصائيات متعددة

يوضح الكود التالي كيفية حساب الخطأ القياسي لكل معامل في نموذج الانحدار الخطي المتعدد:

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

ومن النتائج يمكننا أن نرى:

• المعامل المقدر لتقاطع النموذج هو 29.59985476 والخطأ المعياري لهذا التقدير هو 1.49354577 .
• المعامل المقدر لمتغير التوقع disp في النموذج هو -0.04121512 والخطأ المعياري لهذا التقدير هو 0.00527082 .

يمكننا أيضًا تصور توزيع العينات التمهيدية بسرعة:

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

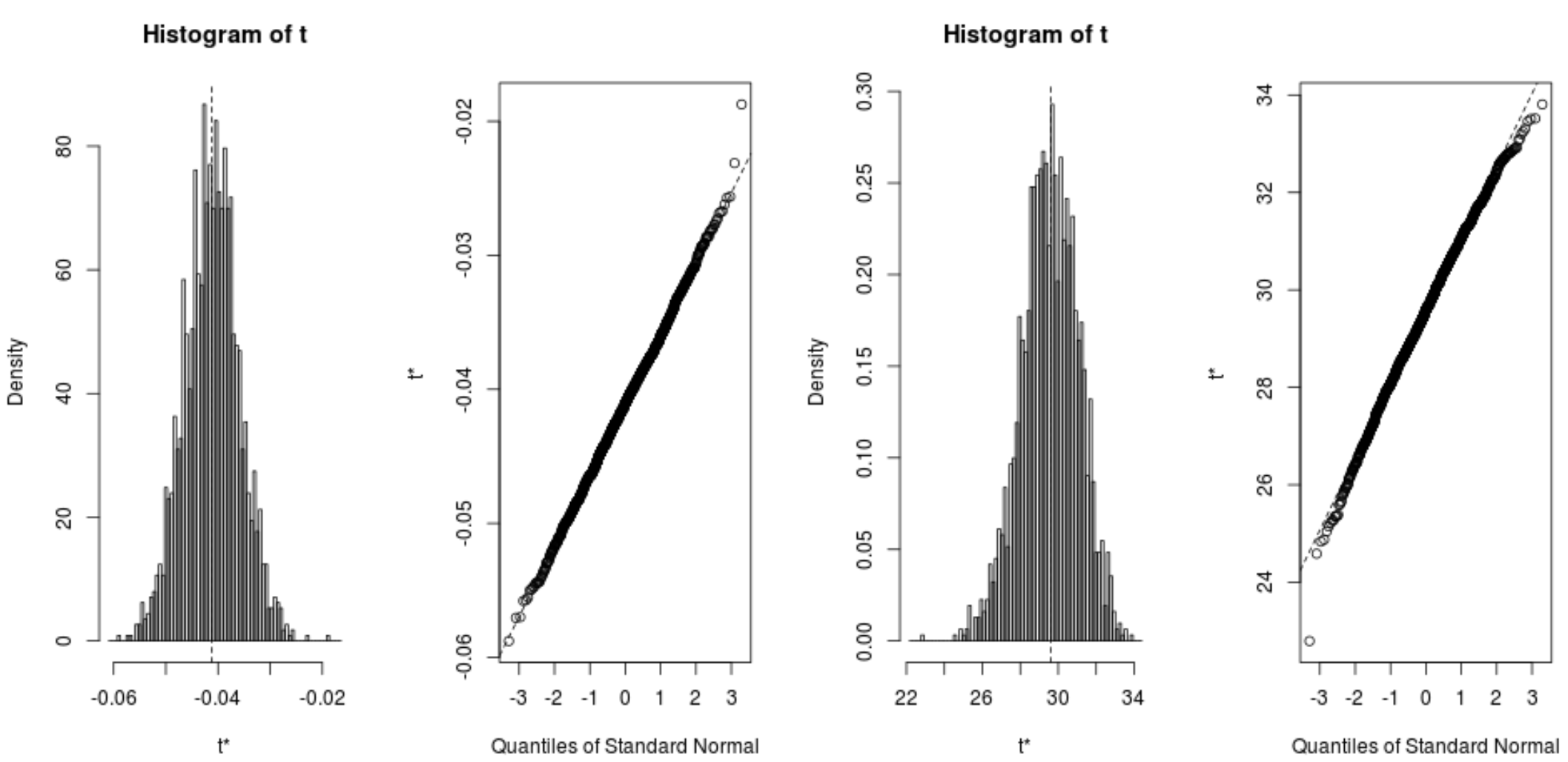
يمكننا أيضًا استخدام الكود التالي لحساب فترات الثقة 95% لكل معامل:

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

من النتائج يمكننا أن نرى أن فترات الثقة 95٪ لمعاملات النموذج هي كما يلي:

• IC للاعتراض: (26.78، 32.66)
• CI للعرض : (-.0520، -.0312)

مصادر إضافية

كيفية إجراء الانحدار الخطي البسيط في R
كيفية إجراء الانحدار الخطي المتعدد في R
مقدمة لفترات الثقة