مقدمة للتوزيع الأسي

التوزيع الأسي هو توزيع احتمالي يستخدم لنمذجة الوقت الذي يتعين علينا انتظاره حتى وقوع حدث معين.

يمكن استخدام هذا التوزيع للإجابة على أسئلة مثل:

• ما المدة التي يجب أن ينتظرها بائع التجزئة حتى يدخل العميل إلى متجره؟
• كم من الوقت سيستمر الكمبيوتر المحمول في العمل قبل أن ينكسر؟
• كم من الوقت ستستمر بطارية السيارة في العمل قبل أن تموت؟
• كم من الوقت يجب أن ننتظر حتى الانفجار البركاني التالي في منطقة معينة؟

في كل سيناريو، نريد حساب المدة التي سننتظرها حتى يقع حدث معين. وبالتالي، يمكن صياغة كل سيناريو باستخدام التوزيع الأسي.

التوزيع الأسي: PDF وCDF

إذا كان المتغير العشوائي X يتبع التوزيع الأسي، فيمكن كتابة دالة الكثافة الاحتمالية لـ X :

و (س؛ ) = e ^-x

ذهب:

• : معلمة المعدل (محسوبة على أنها  = 1/μ)
• e: ثابت يساوي تقريبًا 2.718

دالة التوزيع التراكمي

F (س؛ ) = 1 – ه – ^x

من الناحية العملية، يتم استخدام CDF في أغلب الأحيان لحساب الاحتمالات المتعلقة بالتوزيع الأسي.

على سبيل المثال، لنفترض أن متوسط عدد الدقائق بين ثوران نبع ماء حار معين هو 40 دقيقة. ما مدى احتمالية انتظارنا أقل من 50 دقيقة لحدوث الثوران؟

لحل هذه المشكلة، نحتاج أولاً إلى حساب معامل المعدل:

• lect = 1/μ
• lect = 1/40
• φ = 0.025

يمكننا التعويض بـ lect = 0.025 و x = 50 في صيغة CDF:

• P(X ≥ x) = 1 – ه – ^lectx
• ف(س ≥ 50) = 1 – ه ^-0.025(50)
• ف(س ≥ 50) = 0.7135

احتمال أن ننتظر أقل من 50 دقيقة للثوران التالي هو 0.7135 .

تصور التوزيع الأسي

الرسم البياني التالي يوضح دالة الكثافة الاحتمالية لمتغير عشوائي

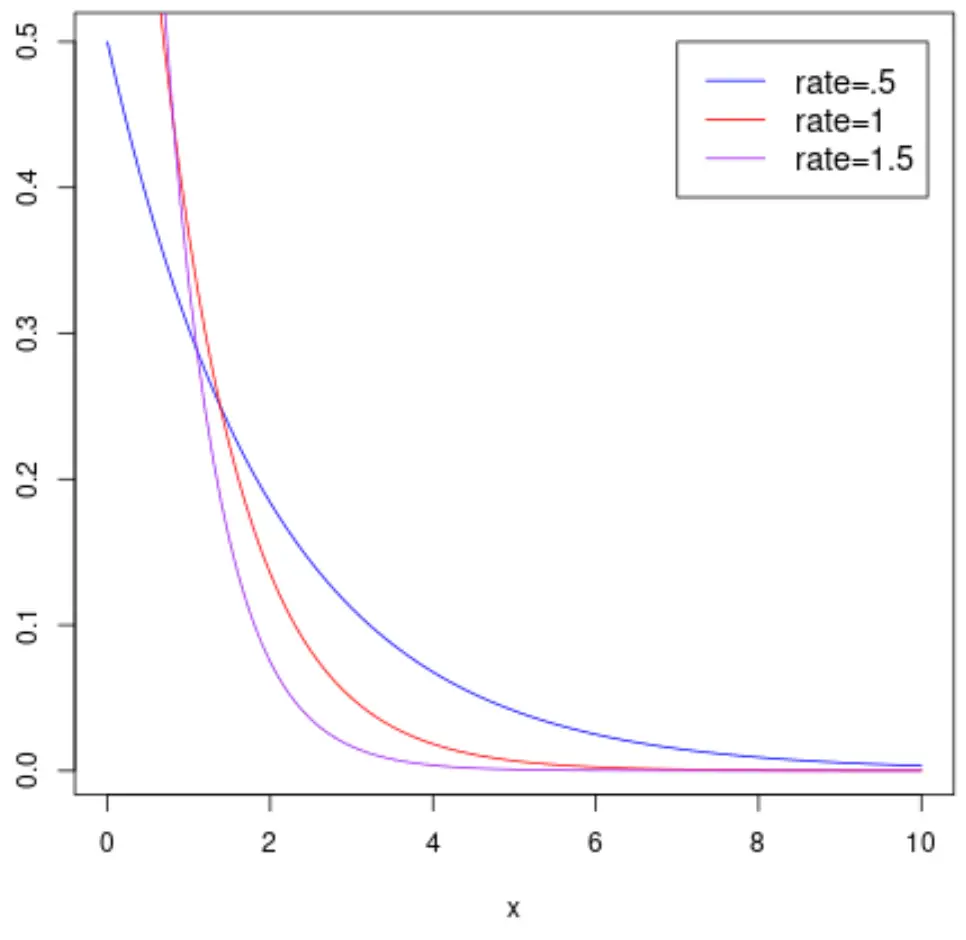
ويوضح الرسم البياني التالي دالة التوزيع التراكمي للمتغير العشوائي X والتي تتبع التوزيع الأسي بمعلمات معدل مختلفة:

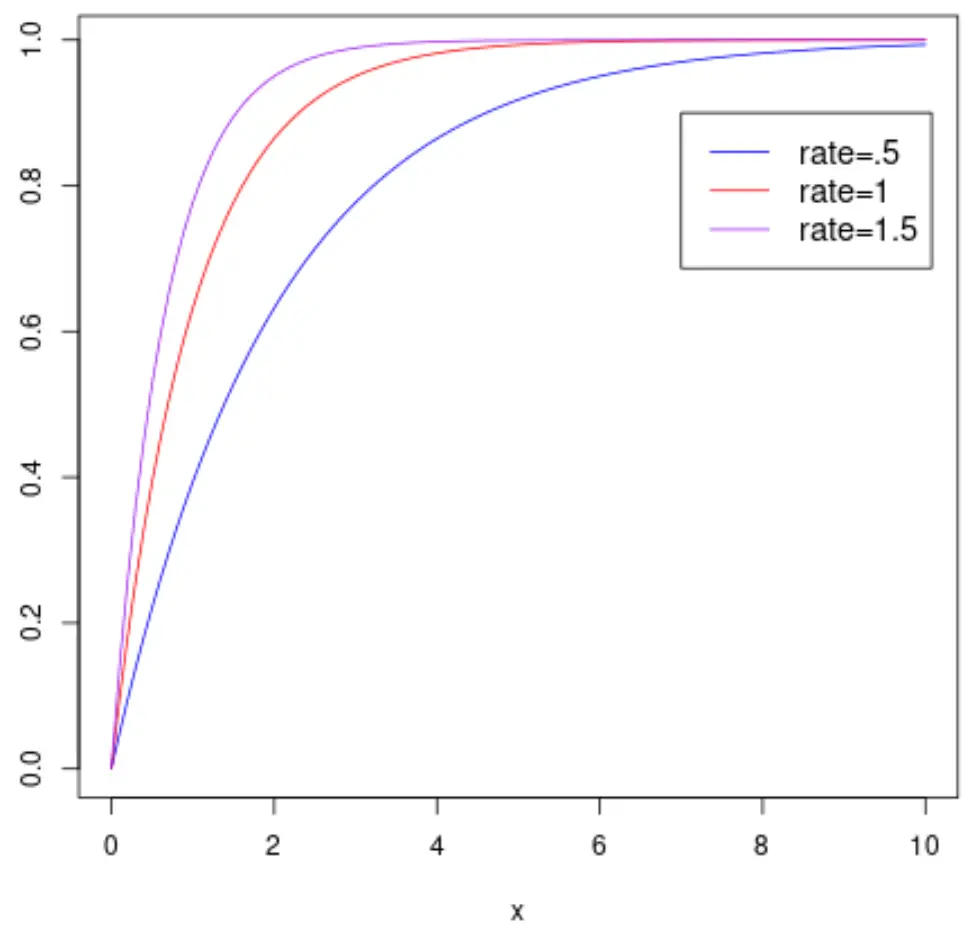
ملاحظة: راجع هذا البرنامج التعليمي لمعرفة كيفية رسم التوزيع الأسي في R.

خصائص التوزيع الأسي

التوزيع الأسي له الخصائص التالية:

• المتوسط: 1/ ε
• الفرق: 1/ ²

على سبيل المثال، لنفترض أن متوسط عدد الدقائق بين ثوران نبع ماء حار معين هو 40 دقيقة. سوف نحسب المعدل كـ 1 = 1/μ = 1/40 = 0.025.

يمكننا بعد ذلك حساب الخصائص التالية لهذا التوزيع:

• متوسط وقت الانتظار للثوران القادم: 1/ 1 = 1 / .025 = 40
• التباين في أوقات الانتظار للثوران التالي: 1/ ² = 1 / .025 ² = 1600

ملاحظة: يحتوي التوزيع الأسي أيضًا على خاصية عديمة الذاكرة ، مما يعني أن احتمال وقوع حدث مستقبلي لا يتأثر بحدوث الأحداث الماضية.

مشاكل ممارسة التوزيع الأسي

استخدم المسائل التدريبية التالية لاختبار معرفتك بالتوزيع الأسي.

السؤال 1: يدخل عميل جديد إلى المتجر كل دقيقتين في المتوسط. بعد وصول العميل، حدد احتمالية وصول عميل جديد في أقل من دقيقة.

الحل 1: متوسط الوقت بين العملاء دقيقتين. وبالتالي يمكن حساب المعدل على النحو التالي:

• lect = 1/μ
• lect = 1/2
• ν = 0.5

يمكننا التعويض بـ 0 = 0.5 و x = 1 في صيغة CDF:

• P(X ≥ x) = 1 – ه – ^lectx
• ف(س ≥ 1) = 1 – ه ^-0.5(1)
• ف(س ≥ 1) = 0.3935

احتمال أن ننتظر أقل من دقيقة حتى يصل العميل التالي هو 0.3935 .

السؤال 2: يحدث زلزال في المتوسط كل 400 يوم في منطقة معينة. بعد وقوع الزلزال، أوجد احتمال مرور أكثر من 500 يوم قبل وقوع الزلزال التالي.

الحل 2: متوسط الوقت بين الزلازل هو 400 يوم. وبالتالي يمكن حساب المعدل على النحو التالي:

• lect = 1/μ
• lect = 1/400
• φ = 0.0025

يمكننا التعويض بـ lect = 0.0025 و x = 500 في صيغة CDF:

• P(X ≥ x) = 1 – ه – ^lectx
• ف(X ≥ 1) = 1 – ه ^-0.0025(500)
• ف(س ≥ 1) = 0.7135

احتمال أن ننتظر أقل من 500 يوم لحدوث الزلزال القادم هو 0.7135. لذا فإن احتمال أن ننتظر أكثر من 500 يوم لحدوث الزلزال القادم هو 1 – 0.7135 = 0.2865 .

السؤال 3: يتلقى مركز الاتصال مكالمة جديدة كل 10 دقائق في المتوسط. بعد أن يتصل العميل، حدد احتمالية اتصال العميل الجديد خلال 10 إلى 15 دقيقة.

الحل 3: متوسط الوقت بين المكالمات هو 10 دقائق. وبالتالي يمكن حساب المعدل على النحو التالي:

• lect = 1/μ
• lect = 1/10
• φ = 0.1

يمكننا استخدام الصيغة التالية لحساب احتمالية اتصال العميل الجديد خلال 10-15 دقيقة:

• ف(10 < X ≥ 15) = (1 – ه ^-0.1(15) ) – (1 – ه ^-0.1(10) )
• ف(10 < X ≥ 15) = 0.7769 – 0.6321
• ف(10 < X ≥ 15) = 0.1448

احتمالية اتصال عميل جديد خلال 10-15 دقيقة. هو 0.1448 .

مصادر إضافية

توفر البرامج التعليمية التالية مقدمات للتوزيعات الاحتمالية الشائعة الأخرى.

مقدمة للتوزيع الطبيعي
مقدمة للتوزيع ذي الحدين
مقدمة لتوزيع بواسون
مقدمة للتوزيع الموحد