التوزيع الأسي

By دكتور بنيامين أندرسون زومار 3, 2023 احتمالا 0 Comments

تشرح هذه المقالة المقصود بالتوزيع الأسي في الإحصائيات وفيم يُستخدم. وبالمثل، ستجد ما هي خصائص التوزيع الأسي بالإضافة إلى صيغه ورسمه البياني وتدريب محلول. بالإضافة إلى ذلك، سوف تكون قادرًا على حساب أي احتمال باستخدام حاسبة التوزيع الأسي عبر الإنترنت.

ما هو التوزيع الأسي؟

التوزيع الأسي هو توزيع احتمالي مستمر يستخدم لنمذجة وقت الانتظار لحدوث ظاهرة عشوائية.

وبشكل أكثر دقة، يسمح لنا التوزيع الأسي بوصف وقت الانتظار بين حدثين يتبعان توزيع بواسون. ولذلك، فإن التوزيع الأسي يرتبط ارتباطًا وثيقًا بتوزيع بواسون.

➤ انظر: ما هو توزيع بواسون؟

يحتوي التوزيع الأسي على معلمة مميزة، ممثلة بالحرف اليوناني α وتشير إلى عدد المرات التي من المتوقع أن يحدث فيها الحدث المدروس خلال فترة زمنية معينة.

$X\sim \text{Exp}(\lambda)$

وبالمثل، يتم استخدام التوزيع الأسي أيضًا لنمذجة الوقت حتى حدوث الفشل. وبالتالي فإن التوزيع الأسي له العديد من التطبيقات في نظرية الموثوقية والبقاء.

أمثلة على التوزيعات الأسية

الآن بعد أن عرفنا تعريف التوزيع الأسي، دعونا نلقي نظرة على عدة أمثلة لهذا النوع من التوزيع لفهم المفهوم بشكل أفضل.

أمثلة على التوزيع الأسي:

الوقت المنقضي بين مكالمتين في مركز الاتصال.
الوقت الذي يجب على الشخص انتظاره حتى مرور سيارة أجرة مجانية في شارع معين.
وقت الانتظار حتى يدخل عميل جديد إلى المتجر.
الوقت المنقضي بين دخول مستخدمين مختلفين إلى صفحة الويب.
الوقت المنقضي في المطار بين إقلاع طائرة ومغادرة أخرى.

صيغة التوزيع الأسي

صيغة دالة الكثافة التي تحدد حساب احتمالية التوزيع الأسي تساوي π مضروبة في الرقم e أس سالب π مضروبة في x.

بمعنى آخر، صيغة حساب احتمال التوزيع الأسي هي كما يلي:

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب احتمال وجود متغير يتبع التوزيع الأسي.

من ناحية أخرى، فإن صيغة حساب الاحتمال التراكمي للتوزيع الأسي هي كما يلي:

$P[X\leq x]=1-e^{-\lambda x}$

الرسم البياني للتوزيع الأسي

في هذا القسم يمكنك رؤية التمثيل الرسومي لوظيفة الكثافة ووظيفة التوزيع للتوزيع الأسي.

يمكنك أدناه أن ترى كيف يختلف الرسم البياني لوظيفة الكثافة للتوزيع الأسي اعتمادًا على قيمة المعلمة lect.

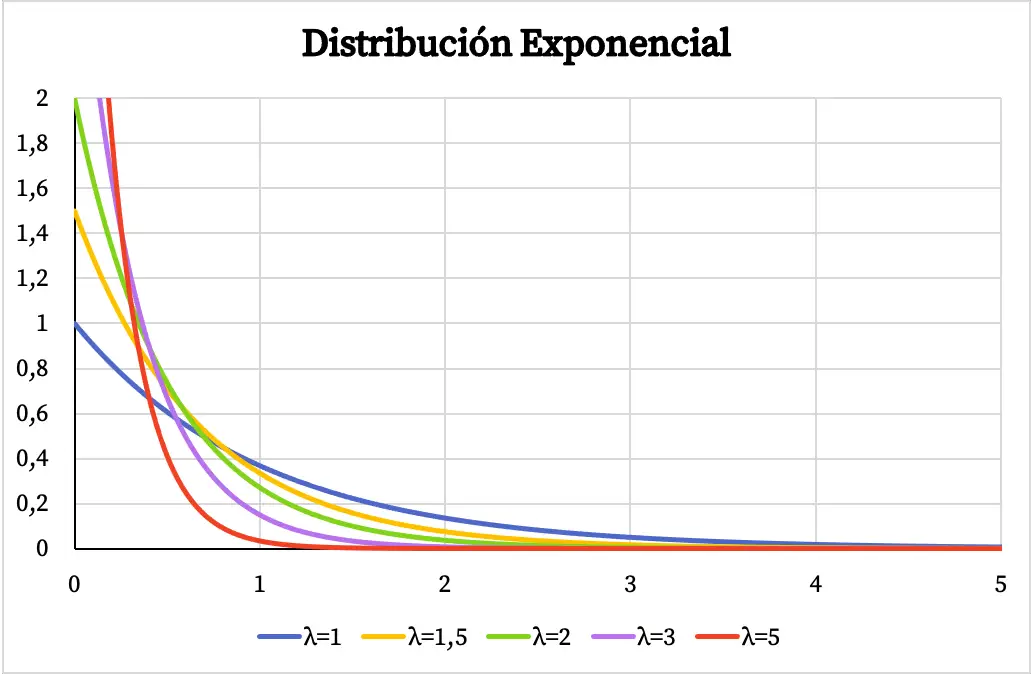
وبالمثل، تعتمد دالة الاحتمال التراكمي للتوزيع الأسي أيضًا على قيمة المعلمة lect، كما ترون في الرسم البياني التالي:

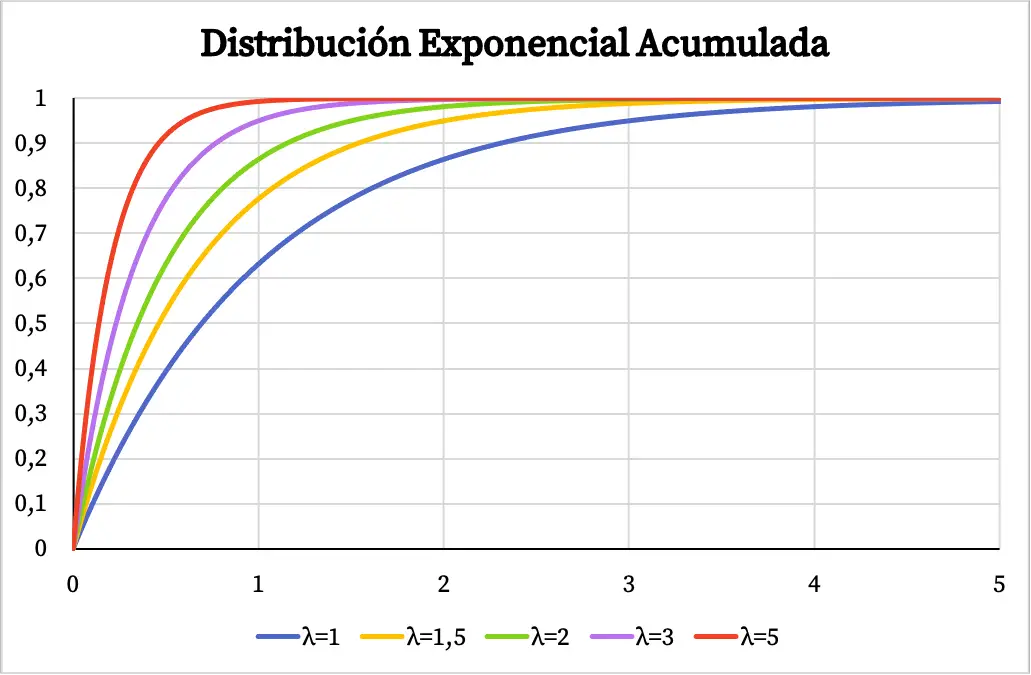
الرسم البياني لاحتمال التوزيع التراكمي الأسي

حل تمرين التوزيع الأسي

في المتوسط، يصل 1=1 مستخدم/دقيقة إلى صفحة ويب محددة. ما احتمال أن يكون الوقت بين دخول مستخدمين 3 دقائق؟ واحتمال أنها تساوي أو تقل عن دقيقتين؟

التوزيع الذي يحدد المتغير العشوائي لهذه المشكلة هو توزيع أسي، حيث أننا ندرس الزمن الذي يمر من لحظة وقوع حدث ما (دخول المستخدم إلى صفحة الويب) حتى حدوث نفس هذا الحدث مرة أخرى.

$X\sim \text{Exp}(1)$

لذلك، لحساب احتمال أن يكون الوقت المنقضي بين دخول مستخدمين مختلفين ثلاث دقائق، نحتاج إلى تطبيق صيغة دالة الكثافة (انظر أعلاه):

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

من ناحية أخرى، لتحديد الاحتمال التراكمي، يجب علينا استخدام صيغة دالة التوزيع للتوزيع الأسي:

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

خصائص التوزيع الأسي

يتميز التوزيع الأسي بالخصائص التالية:

يحتوي التوزيع الأسي على معلمة مميزة، ، والتي تشير إلى عدد المرات التي من المتوقع أن تحدث فيها الظاهرة المدروسة خلال فترة زمنية معينة.

$X\sim \text{Exp}(\lambda)$

لا يمكن للتوزيع الأسي أن يأخذ قيمة سالبة، لذا فإن مجال التوزيع الأسي يتكون من جميع الأعداد الحقيقية الأكبر من أو تساوي الصفر.

$x\in [0,+\infty)$

متوسط التوزيع الأسي يساوي واحدًا مقسومًا على المعلمة المميزة lect.

$E[X]=\cfrac{1}{\lambda}$

تباين التوزيع الأسي هو مربع متوسطه، وبالتالي فإن تباين التوزيع الأسي يعادل واحدًا على المعامل lect مربع.

$Var(X)=\cfrac{1}{\lambda^2 }$

مهما كانت قيمة π، فإن معامل عدم التماثل للتوزيع الأسي يساوي دائمًا 2.

$A=2$

وبالمثل، فإن معامل التفرطح لأي توزيع أسي يساوي دائمًا 9.

$C=9$

صيغة دالة الكثافة للتوزيع الأسي هي:

$P[X=x]=\lambda e^{-\lambda x}$

بينما تكون صيغة دالة الاحتمال التراكمي للتوزيع الأسي كما يلي:

$P[X\leq x]=1-e^{-\lambda x}$

يعد التوزيع الأسي أحد التوزيعات الاحتمالية القليلة التي تتمتع بخاصية نفاد الذاكرة. وتعني هذه الخاصية أن وقوع حدث سابق لا يؤثر على احتمالية وقوع ذلك الحدث في المستقبل. على سبيل المثال، في التوزيع الأسي، لا يعتمد احتمال وصول مستخدم جديد إلى صفحة ويب في أقل من دقيقة على ما إذا كان المستخدم قد دخل للتو أو لم يدخل أي مستخدم منذ ذلك الحين. أكثر من عشر دقائق.

$P[X>x+y|X>y]=P[X>x]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”254″ style=”vertical-align: -5px;”></p> </p> <h2 class=$ حاسبة التوزيع الأسي

أدخل قيمة المعلمة lect وقيمة x في الآلة الحاسبة التالية لحساب الاحتمال. تحتاج إلى تحديد الاحتمالية التي تريد حسابها وإدخال الأرقام باستخدام النقطة كفاصل عشري، على سبيل المثال 0.50.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر