التوزيع الطبيعي والتوزيع t: ما الفرق؟

التوزيع الطبيعي هو التوزيع الأكثر استخدامًا في جميع الإحصائيات، ومن المعروف أنه متماثل وعلى شكل جرس.

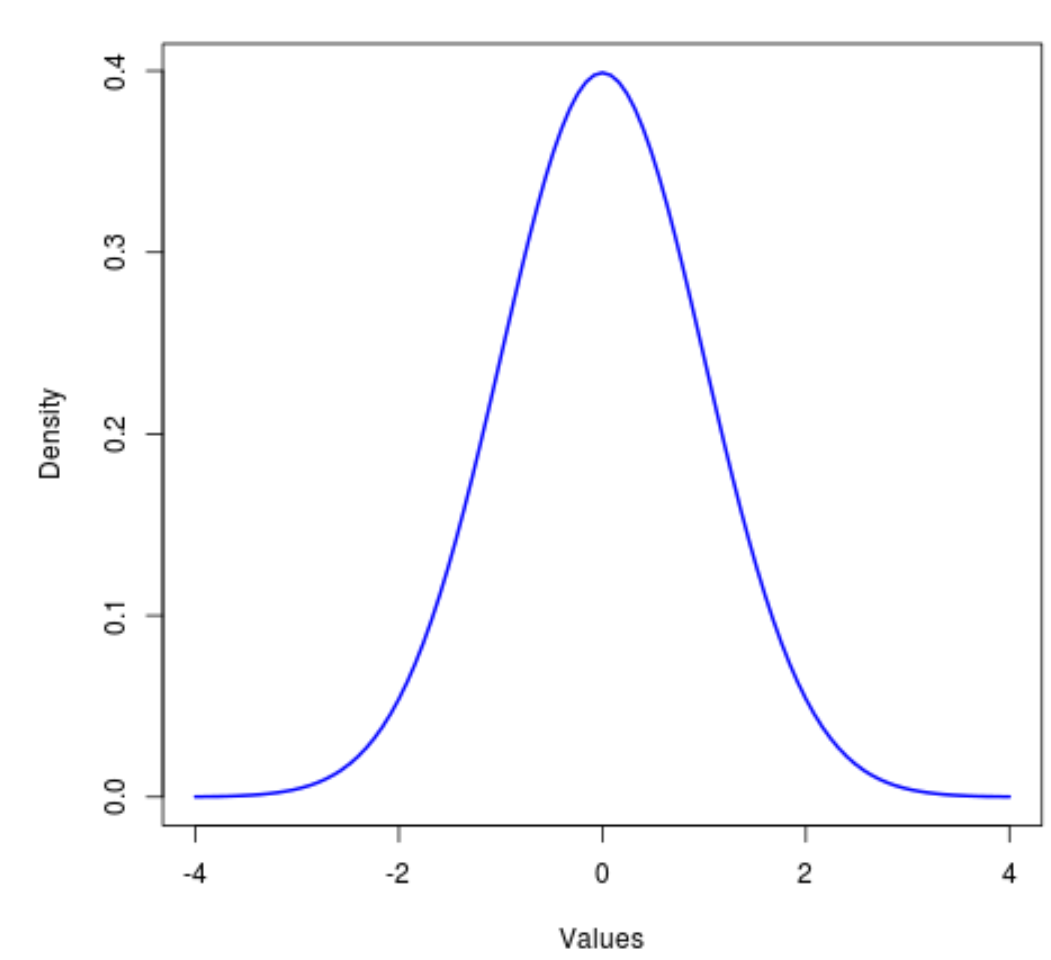
التوزيع ذو الصلة الوثيقة هو توزيع t ، وهو أيضًا متماثل وعلى شكل جرس ولكن له “ذيول” أثقل من التوزيع الطبيعي.

بمعنى آخر، توجد قيم في التوزيع في الأطراف أكثر من القيم الموجودة في المركز مقارنة بالتوزيع الطبيعي:

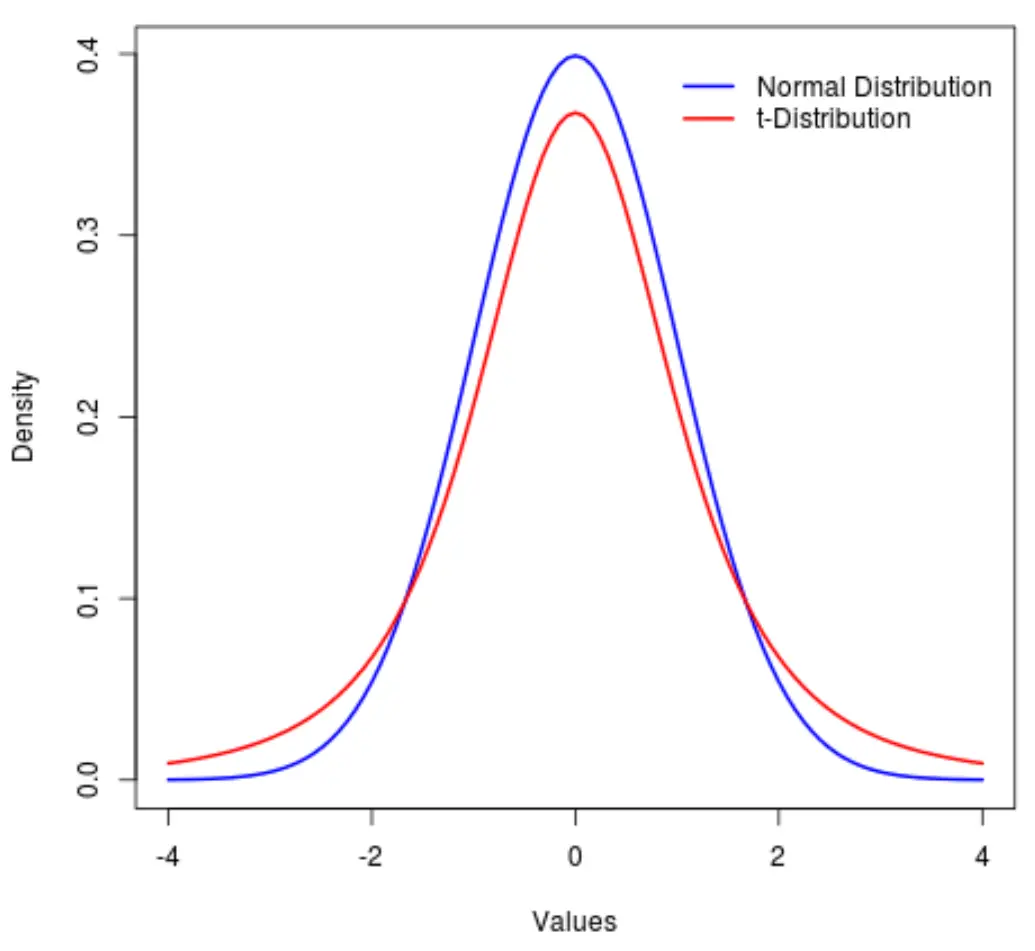
في المصطلحات الإحصائية، نستخدم مقياسًا يسمى التفرطح لقياس مدى “ثقل” التوزيع. لذلك، يمكننا القول أن التفرطح في توزيع t أكبر من التوزيع الطبيعي.

من الناحية العملية، غالبًا ما نستخدم توزيع t عند إجراء اختبار الفرضيات أو إنشاء فترات الثقة .

على سبيل المثال، صيغة حساب فاصل الثقة لمتوسط المحتوى هي:

فاصل الثقة = x +/- t _{1-α/2, n-1} *(s/√ n )

ذهب:

• x : متوسط العينة
• t: قيمة t الحرجة، بناءً على مستوى الأهمية α وحجم العينة n
• s: عينة الانحراف المعياري
• ن: حجم العينة

في هذه الصيغة، نستخدم القيمة الحرجة للجدول t بدلاً من القيمة الحرجة للجدول z عندما يتحقق أحد الشروط التالية:

• نحن لا نعرف الانحراف المعياري للسكان.
• حجم العينة أقل من أو يساوي 30.

يوفر المخطط الانسيابي التالي طريقة مفيدة لمعرفة ما إذا كان يجب عليك استخدام القيمة الحرجة من الجدول t أو الجدول z:

والفرق الرئيسي بين استخدام توزيع t واستخدام التوزيع الطبيعي عند إنشاء فترات الثقة هو أن القيم الحرجة لتوزيع t ستكون أكبر، مما يؤدي إلى فترات ثقة أوسع .

على سبيل المثال، لنفترض أننا نريد إنشاء فاصل ثقة بنسبة 95% لمتوسط وزن مجموعة من السلاحف، من أجل جمع عينة عشوائية من السلاحف بالمعلومات التالية:

• حجم العينة ن = 25
• متوسط وزن العينة س = 300
• عينة الانحراف المعياري ق = 18.5

قيمة z الحرجة لمستوى ثقة 95% هي 1.96 بينما قيمة t الحرجة لفترة ثقة 95% مع df = 25-1 = 24 درجة حرية هي 2.0639 .

ومن ثم، فإن فاصل الثقة 95% لمتوسط المحتوى باستخدام القيمة الحرجة z هو:

95% CI = 300 +/- 1.96*(18.5/√ 25 ) = [292.75, 307.25]

في حين أن فاصل الثقة 95% للمجتمع يعني استخدام قيمة t الحرجة:

95% CI = 300 +/- 2.0639*(18.5/√25) = [292.36, 307.64]

لاحظ أن فاصل الثقة مع القيمة الحرجة t أوسع.

الفكرة هنا هي أنه عندما يكون لدينا أحجام عينة صغيرة، فإننا نكون أقل ثقة في المتوسط السكاني الحقيقي، لذلك من المفيد استخدام توزيع t لإنتاج فترات ثقة أوسع تتمتع بفرص أكبر لاحتواء متوسط السكان الحقيقي.

تصور درجات الحرية لتوزيع t

وتجدر الإشارة إلى أنه مع زيادة درجات الحرية يقترب توزيع t من التوزيع الطبيعي.

لتوضيح ذلك أنظر إلى الرسم البياني التالي الذي يوضح شكل توزيع t مع درجات الحرية التالية:

• مدافع = 3
• مدافع = 10
• مدافع = 30

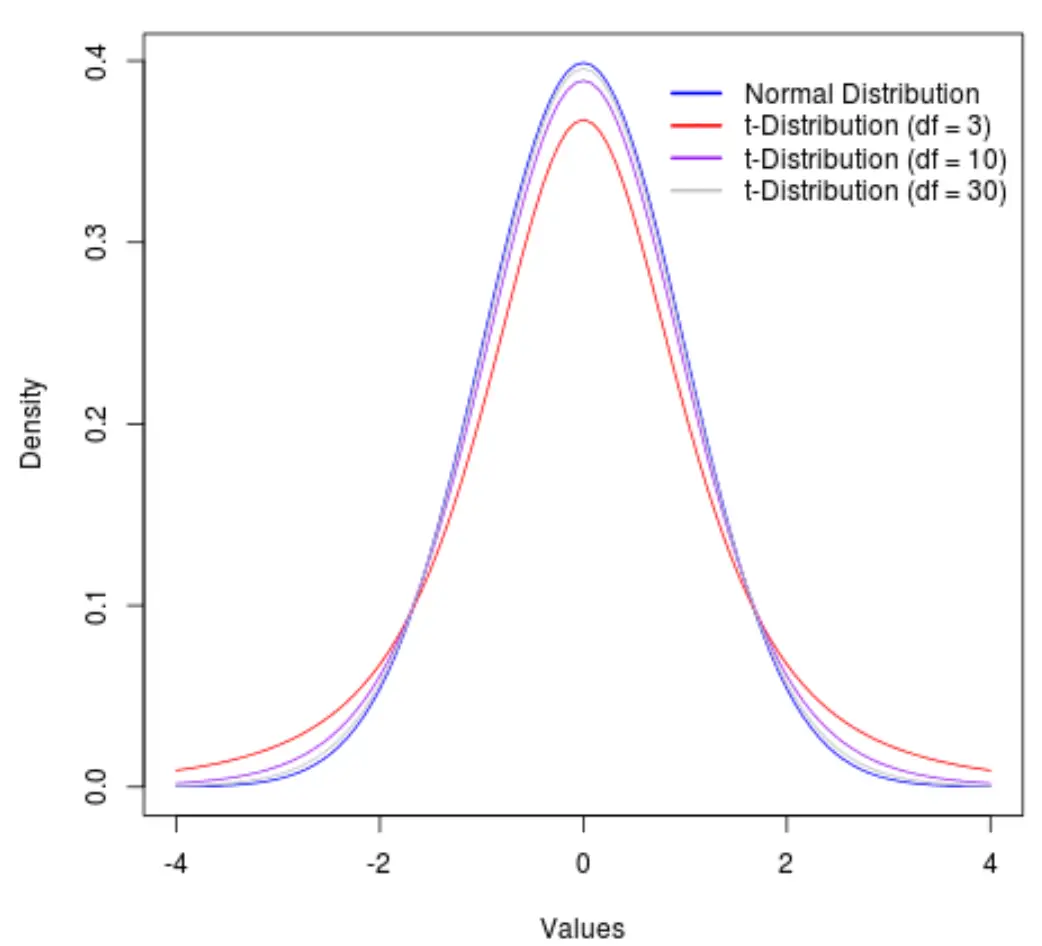
بعد 30 درجة من الحرية، يصبح توزيع t والتوزيع الطبيعي متشابهين للغاية بحيث تصبح الاختلافات بين استخدام قيمة t الحرجة وقيمة z الحرجة في الصيغ ضئيلة.