التوزيع الطبيعي والتوزيع الطبيعي القياسي: الفرق

التوزيع الطبيعي هو التوزيع الاحتمالي الأكثر استخدامًا في الإحصاء.

لديها الخصائص التالية:

• متماثل
• على شكل جرس
• المتوسط والوسيط متساويان؛ كلاهما يقع في وسط التوزيع

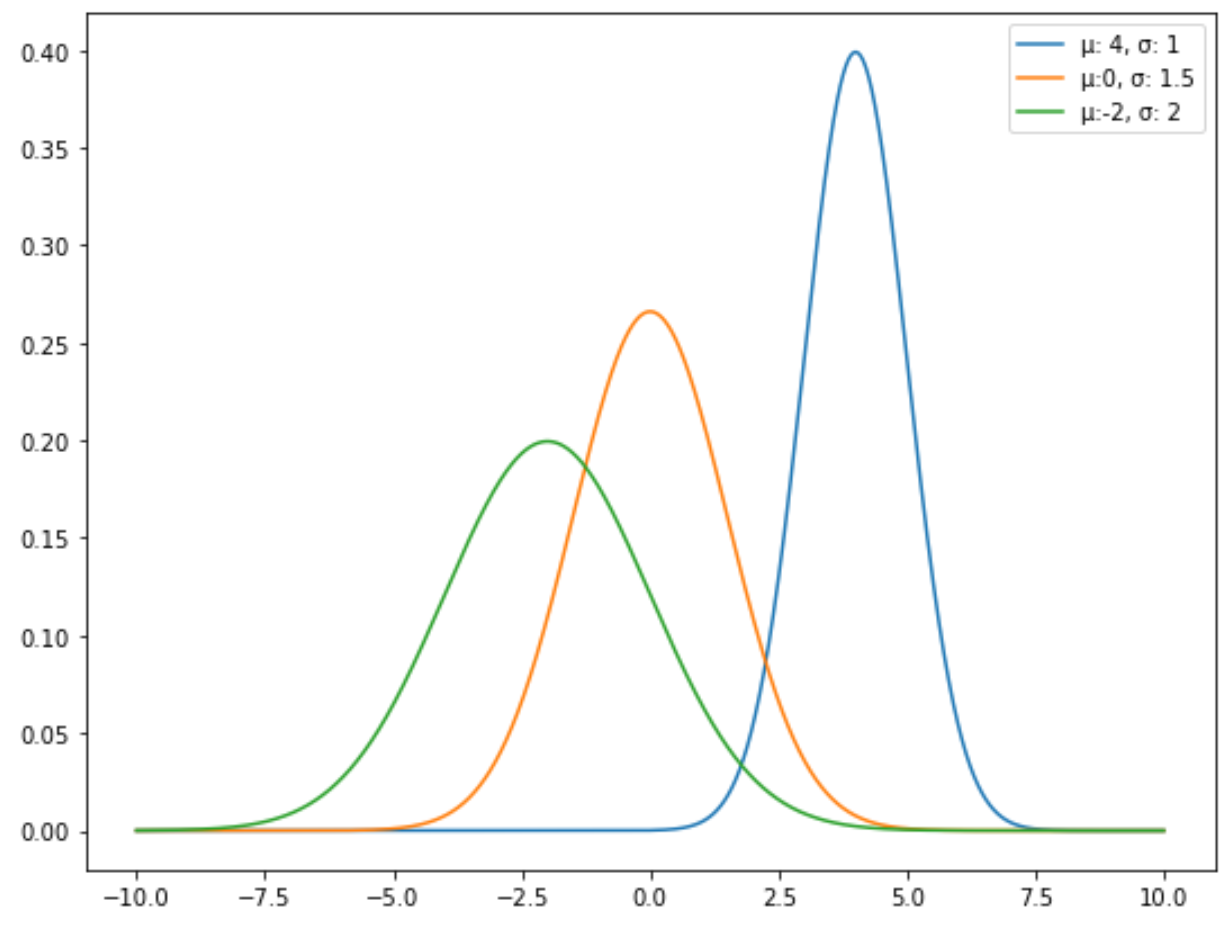
متوسط التوزيع الطبيعي يحدد موقعه والانحراف المعياري يحدد انتشاره.

على سبيل المثال، يوضح الرسم البياني التالي ثلاثة توزيعات طبيعية بوسائل وانحرافات معيارية مختلفة:

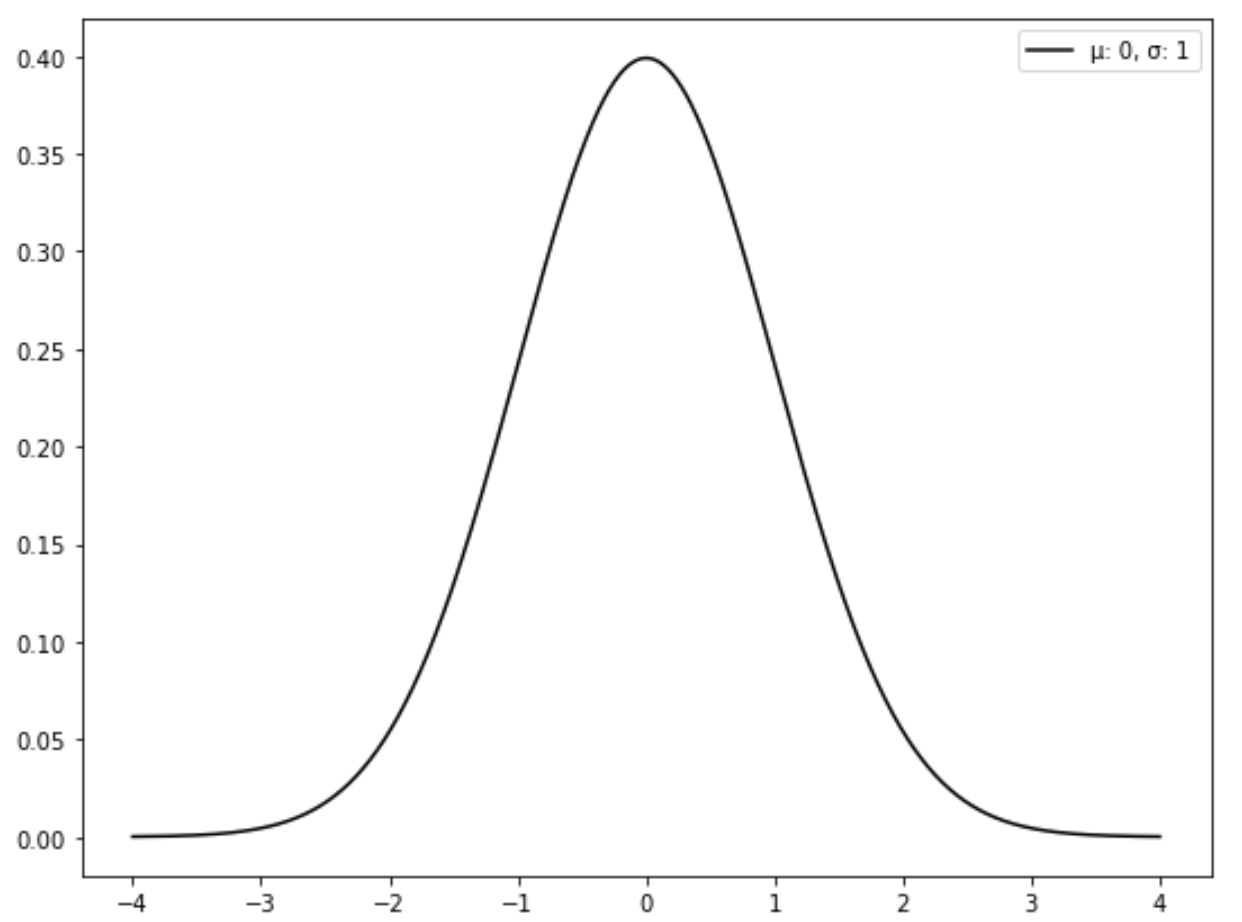
التوزيع الطبيعي المعياري هو نوع محدد من التوزيع الطبيعي حيث يكون المتوسط 0 والانحراف المعياري هو 1.

ويوضح الرسم البياني التالي التوزيع الطبيعي القياسي:

كيفية تحويل التوزيع الطبيعي إلى التوزيع الطبيعي القياسي

يمكن تحويل أي توزيع طبيعي إلى توزيع طبيعي قياسي عن طريق تحويل قيم البيانات إلى نقاط z، باستخدام الصيغة التالية:

ض = (س – μ) / σ

ذهب:

• x: قيمة البيانات الفردية
• μ: متوسط التوزيع
• σ : الانحراف المعياري للتوزيع

على سبيل المثال، لنفترض أن لدينا مجموعة البيانات التالية بمتوسط 6 وانحراف معياري قدره 2.152:

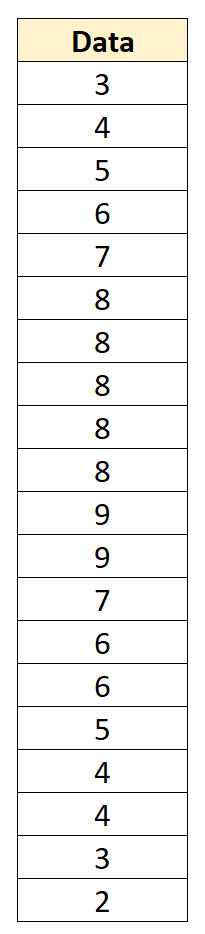
يمكننا تحويل كل قيمة بيانات فردية إلى درجة Z عن طريق طرح 6 من كل قيمة والقسمة على 2.152:

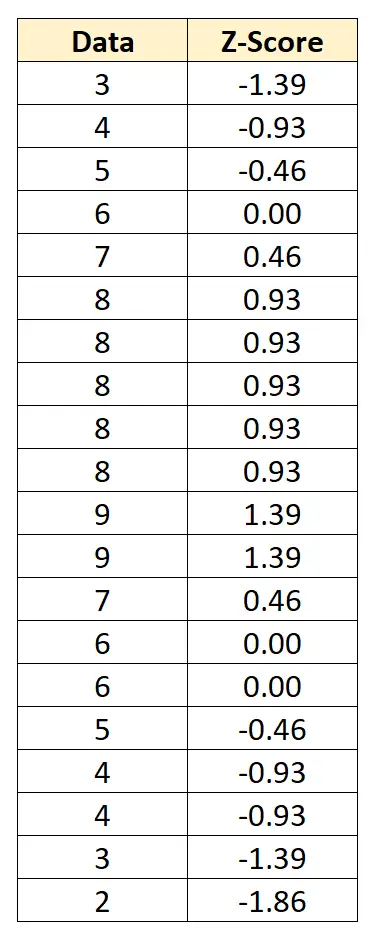
تخبرنا النتيجة z بعدد الانحرافات المعيارية لكل نقطة بيانات عن المتوسط. على سبيل المثال، قيمة البيانات الأولى “3” هي 1.39 انحرافات معيارية أقل من المتوسط.

متوسط توزيع الدرجات هذا له متوسط صفر وانحراف معياري واحد.

كيفية استخدام التوزيع الطبيعي القياسي

التوزيع الطبيعي القياسي له الخصائص التالية:

• يقع حوالي 68% من البيانات ضمن انحراف معياري واحد عن المتوسط
• يقع حوالي 95% من البيانات ضمن انحرافين معياريين عن المتوسط.
• يقع حوالي 99.7% من البيانات ضمن ثلاثة انحرافات معيارية عن المتوسط.

يُعرف هذا بالقاعدة الأساسية ويستخدم لفهم توزيع القيم في مجموعة البيانات.

على سبيل المثال، لنفترض أن ارتفاع النباتات في حديقة معينة يتم توزيعه بشكل طبيعي بمتوسط 47.4 بوصة وانحراف معياري قدره 2.4 بوصة.

باستخدام القاعدة العامة، ما هي النسبة المئوية للنباتات التي يقل طولها عن 54.6 بوصة؟

تنص القاعدة الأساسية على أنه بالنسبة لمجموعة بيانات معينة ذات توزيع طبيعي، فإن 99.7% من قيم البيانات تقع ضمن ثلاثة انحرافات معيارية عن المتوسط. وهذا يعني أن 49.85% من القيم تقع بين المتوسط وثلاثة انحرافات معيارية فوق المتوسط.

في هذا المثال، 54.6 هو ثلاثة انحرافات معيارية فوق المتوسط. وبما أننا نعلم أن 50% من قيم البيانات أقل من المتوسط في التوزيع الطبيعي، فإن المجموع 50% + 49.85% = 99.85% من القيم أقل من 54.6.

لذا فإن 99.85% من النباتات يقل طولها عن 54.6 بوصة.

مصادر إضافية

مشاكل في ممارسة قواعد الإبهام
قواعد حاسبة الإبهام
كيفية تطبيق القاعدة الأساسية في Excel