التوزيع الطبيعي أو الموحد: ما الفرق؟

التوزيع الطبيعي هو التوزيع الاحتمالي الأكثر استخدامًا في الإحصاء.

لديها الخصائص التالية:

• متماثل
• على شكل جرس

إذا قمنا بإنشاء مخطط للتوزيع الطبيعي، فسيبدو كما يلي:

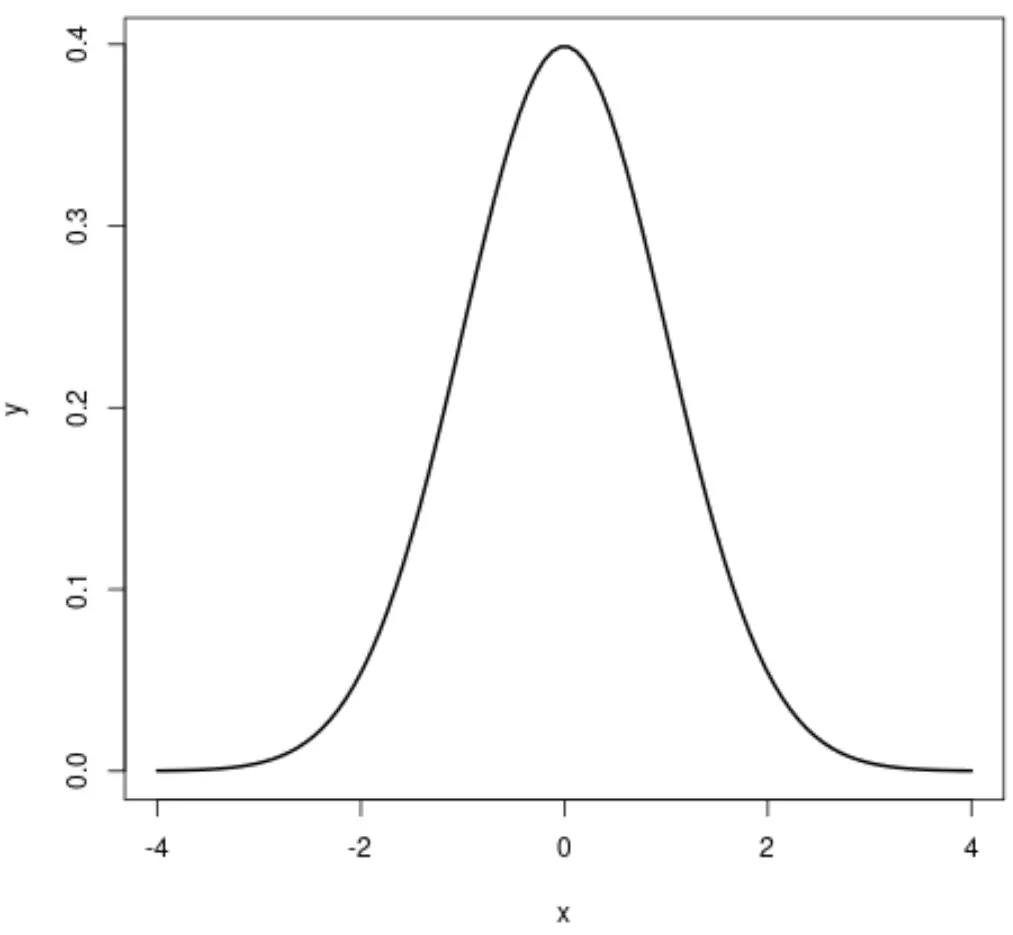
التوزيع الموحد هو توزيع احتمالي يكون فيه لكل قيمة بين الفترة من a إلى b نفس احتمال الحدوث.

لديها الخصائص التالية:

• متماثل
• مستطيلة الشكل

إذا قمنا بإنشاء مخطط التوزيع الموحد، فسيبدو كما يلي:

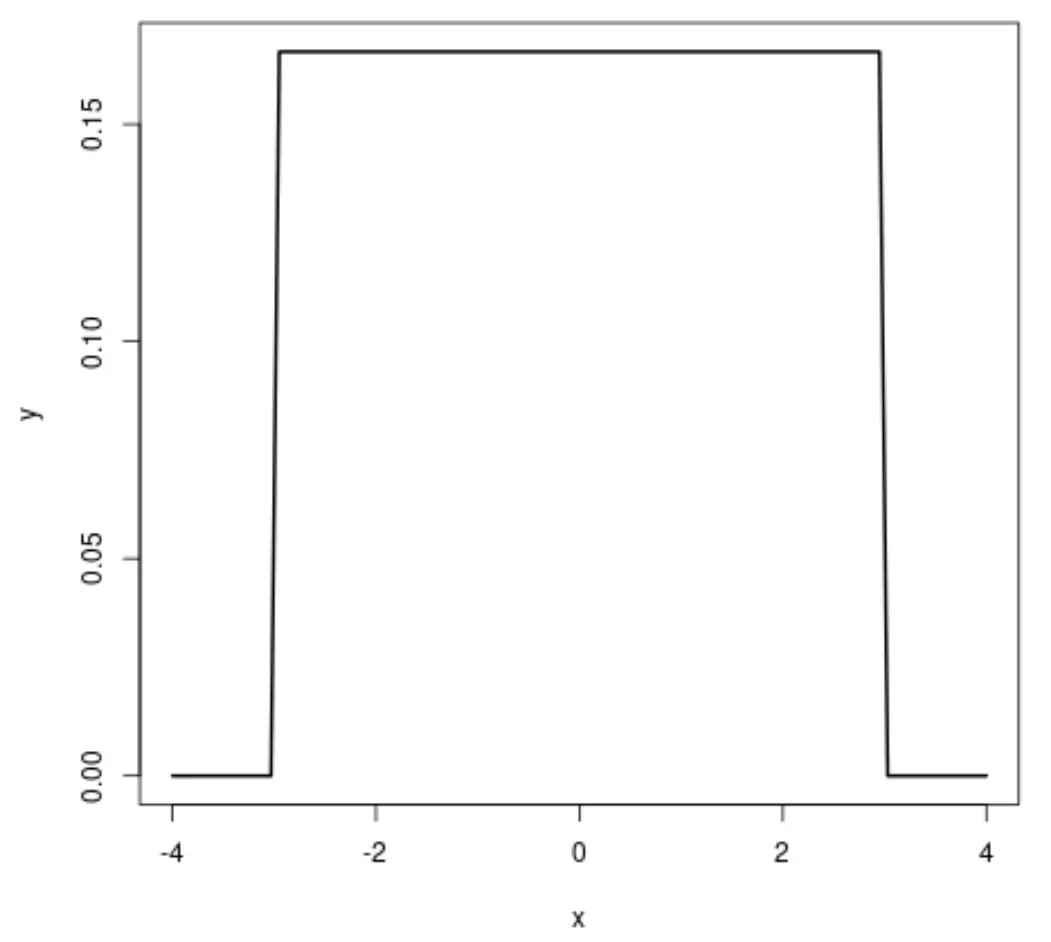
التوزيع الطبيعي والتوزيع الموحد يشتركان في التشابه التالي:

• التوزيعان متماثلان. أي أننا إذا أردنا رسم خط عبر مركز التوزيع، فإن الجانبين الأيسر والأيمن للتوزيع سيعكسان بعضهما البعض بشكل مثالي:

ومع ذلك، فإن التوزيعتين لديهما الفرق التالي:

• التوزيعات لها أشكال مختلفة.
• التوزيع الطبيعي على شكل جرس، مما يعني أن القيم القريبة من مركز التوزيع أكثر احتمالية لحدوثها من القيم الموجودة في أطراف التوزيع.
• التوزيع المنتظم مستطيل الشكل، مما يعني أن كل قيمة في التوزيع لها نفس احتمال حدوثها.

التوزيع الطبيعي أو التوزيع الموحد: متى نستخدمهما؟

يُستخدم التوزيع الطبيعي لنمذجة الظواهر التي تميل إلى اتباع شكل “منحنى الجرس”. على سبيل المثال، من الموثق جيدًا أن وزن الأطفال حديثي الولادة يتم توزيعه عادةً بمتوسط حوالي 7.5 رطل.

يعرض الرسم البياني للوزن عند الولادة للأطفال حديثي الولادة في الولايات المتحدة شكل جرس يتوافق عمومًا مع التوزيع الطبيعي:

ربما يزن معظم الأطفال حوالي 7.5 رطل، ويزن عدد قليل منهم أقل من 7 أرطال والبعض الآخر يزن أكثر من 8 أرطال.

وعلى العكس من ذلك، يتم استخدام التوزيع الموحد لنموذج السيناريوهات التي تكون فيها كل نتيجة محتملة متساوية في الاحتمال.

والمثال الكلاسيكي هو رمي النرد. إذا قمت برمي حجر النرد مرة واحدة، فإن احتمال سقوطه على رقم يقع بين 1 و 6 يتبع توزيعًا منتظمًا لأن كل رقم له نفس احتمال الظهور.

على سبيل المثال، هناك 6 أرقام محتملة يمكن للنرد أن يستقر عليها، لذا فإن احتمال ظهور 1 هو 1/6.

وبالمثل، فإن احتمال حصولك على 2 هو 1/6.

وبالمثل، فإن احتمال حصولك على 3 هو 1/6.

وما إلى ذلك وهلم جرا.

المكافأة: كيفية رسم التوزيع الطبيعي والموحد

استخدمنا الكود التالي في R لإنشاء مخططات للتوزيعات العادية والموحدة:

 #define x-axis
x <- seq(-4, 4, length=100)

#calculate normal distribution probabilities
y <- dnorm(x)

#plot normal distribution
plot(x, y, type = " l ", lwd = 2 )

#define x-axis
x <- seq(-4, 4, length=100)

#calculate uniform distribution probabilities
y <- dunif(x, min = -3, max = 3)

#plot uniform distribution
plot(x, y, type = " l ", lwd = 2 , xlim = c(-4, 4))

مصادر إضافية

6 أمثلة ملموسة للتوزيع الطبيعي
5 أمثلة ملموسة للتوزيع الموحد
التوزيع المتماثل: التعريف + الأمثلة