ما هو التوزيع القاطع؟

التوزيع الفئوي هو توزيع احتمالي منفصل يصف احتمال أن يأخذ المتغير العشوائي قيمة تنتمي إلى إحدى فئات K ، حيث ترتبط كل فئة باحتمال.

لكي يتم تصنيف التوزيع على أنه توزيع فئوي، يجب أن يستوفي المعايير التالية:

• الفئات منفصلة.
• هناك فئتان محتملتان أو أكثر.
• يجب أن يكون احتمال أن يأخذ المتغير العشوائي قيمة في كل فئة بين 0 و 1.
• مجموع الاحتمالات لجميع الفئات يجب أن يصل إلى 1.

المثال الأكثر وضوحًا للتوزيع الفئوي هو توزيع النتائج المرتبطة برمي حجر النرد. هناك K = 6 نتائج محتملة واحتمال كل نتيجة هو 1/6:

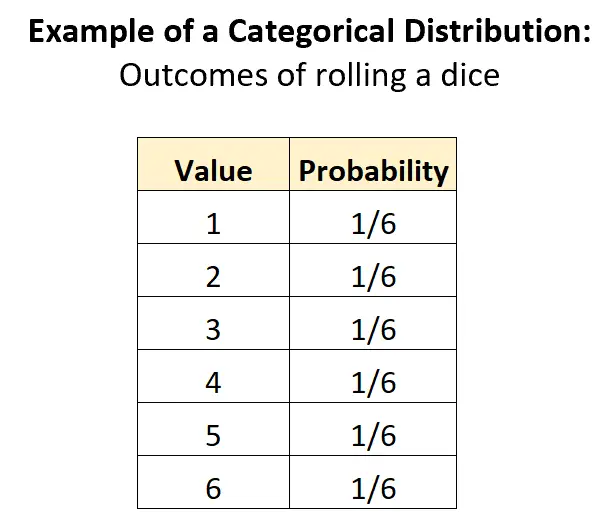
يلبي هذا التوزيع جميع المعايير التي يجب تصنيفها كتوزيع فئوي:

• الفئات منفصلة (على سبيل المثال يمكن للمتغير العشوائي أن يأخذ قيمًا منفصلة فقط – 1، 2، 3، 4، 5، 6)
• هناك فئتان محتملتان أو أكثر.
• احتمال كل فئة يتراوح بين 0 و 1.
• مجموع الاحتمالات هو 1: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

قاعدة عامة:

إذا كان بإمكانك حساب عدد النتائج، فأنت تعمل مع متغير عشوائي منفصل – على سبيل المثال، حساب عدد المرات التي تظهر فيها العملة المعدنية.

ولكن إذا كان بإمكانك قياس النتيجة، فأنت تعمل مع متغير عشوائي مستمر – على سبيل المثال قياس الطول والوزن والوقت وما إلى ذلك.

أمثلة أخرى على التوزيعات الفئوية

هناك العديد من التوزيعات الفئوية في العالم الحقيقي، بما في ذلك:

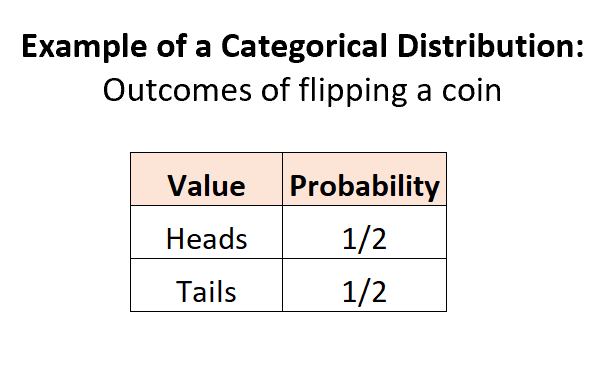
مثال 1: اقلب عملة معدنية.

عندما نقوم برمي عملة معدنية، هناك نتيجتين منفصلتين محتملتين، واحتمال كل نتيجة يتراوح بين 0 و1، ومجموع الاحتمالات يساوي 1:

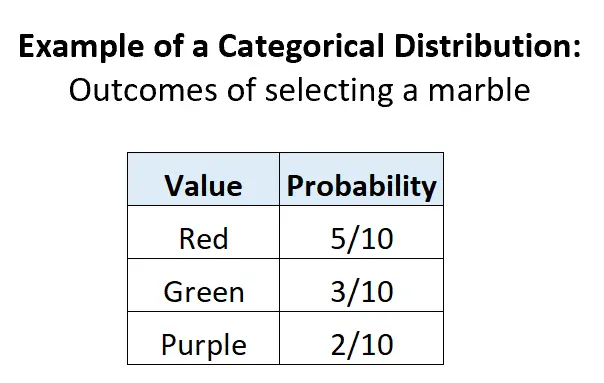
مثال 2: اختيار الرخام في جرة.

لنفترض أن جرة تحتوي على 5 كرات حمراء، و3 كرات خضراء، و2 كرات أرجوانية. إذا اخترنا كرة من الجرة بشكل عشوائي، فهناك 3 نتائج منفصلة محتملة، واحتمال كل نتيجة يتراوح بين 0 و1، ومجموع الاحتمالات يساوي 1:

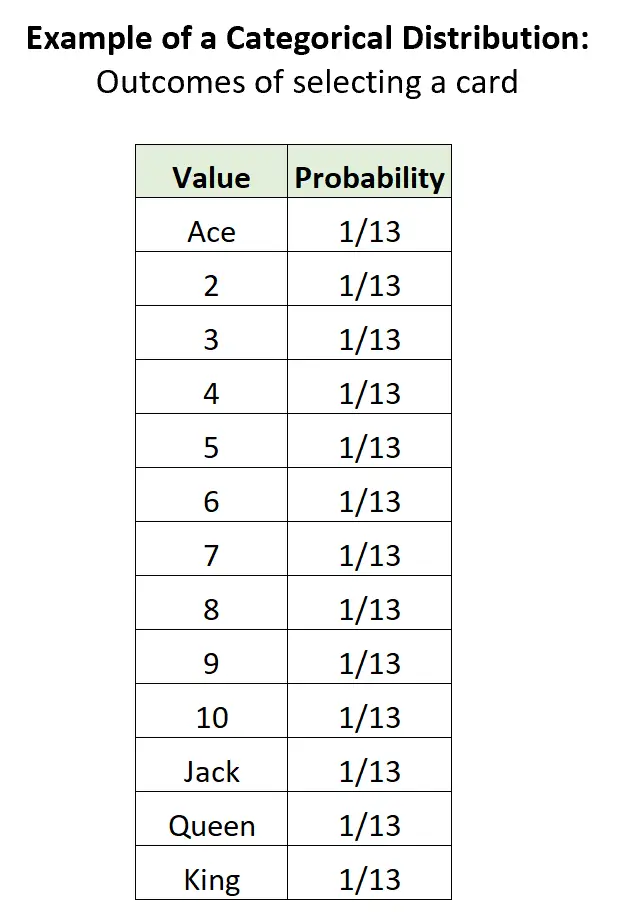
مثال 3: اختيار بطاقة من المجموعة.

إذا اخترنا بطاقة بشكل عشوائي من مجموعة قياسية مكونة من 52 بطاقة، فهناك 13 نتيجة منفصلة محتملة، واحتمال كل نتيجة يتراوح بين 0 و1، ومجموع الاحتمالات يساوي 1:

العلاقة مع التوزيعات الأخرى

لكي يتم تصنيف التوزيع على أنه توزيع فئوي ، يجب أن يحتوي على نتائج محتملة K ≥ 2 وتجربة n = 1.

وباستخدام هذا المصطلح، يكون التوزيع الفئوي مشابهًا للتوزيعات التالية:

توزيع برنولي: K = نتيجتين، n = اختبار واحد

التوزيع ذو الحدين: K = 2 نقطة نهاية، n ≥ 1 تجربة

التوزيع متعدد الحدود: نتائج K ≥ 2، تجربة n ≥

مصادر إضافية

ما هي المتغيرات العشوائية؟
مقدمة للتوزيع ذي الحدين
مقدمة للتوزيع متعدد الحدود