توزيع متماثل

في هذه المقالة، ستتعرف على التوزيعات المتماثلة، وأمثلة على التوزيعات المتماثلة، وكيفية تحديد ما إذا كان التوزيع متماثلًا أم غير متماثل.

ما هو التوزيع المتماثل؟

في الإحصاء، التوزيع المتماثل هو التوزيع الذي يحتوي على نفس عدد القيم الموجودة على يسار الوسط كما على يمين المتوسط. وبعبارة أخرى، في التوزيع المتماثل، المتوسط هو محور التماثل.

على سبيل المثال، التوزيع الطبيعي هو توزيع متماثل.

في جميع التوزيعات المتماثلة، المتوسط يساوي الوسيط. ولكن إذا كان التوزيع أيضًا أحادي الواسطة (الوضع الإحصائي هو قيمة واحدة)، فإن المتوسط والوسيط والمنوال متكافئان.

منطقيًا، لفهم معنى التوزيع المتماثل بشكل كامل، يجب أن تكون واضحًا بشأن معنى المتوسط والوسيط والمنوال. يمكنك مراجعة معنى هذه المفاهيم الإحصائية هنا:

أمثلة على التوزيعات المتماثلة

وبالنظر إلى تعريف التوزيع المتماثل، يظهر أدناه مثال على هذا النوع من التوزيع:

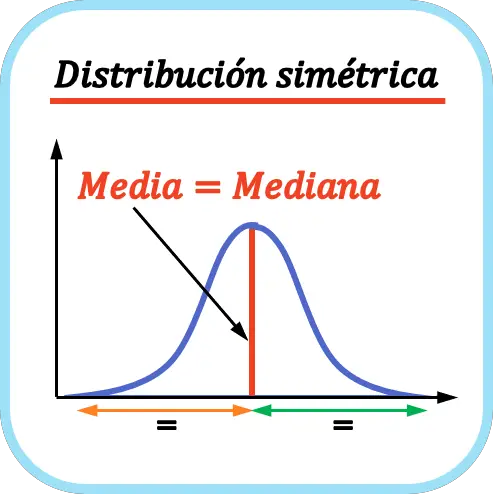
كما يوضح الرسم البياني، التوزيع متماثل لأن المتوسط يقع في منتصف جميع البيانات، أي أن الذيل الموجود على يسار المنحنى هو نفس الذيل الموجود على اليمين. في هذه الحالة، يكون المتوسط والوسيط والمنوال هو نفسه لأن المنوال أحادي الواسطة.

هناك مثالان واضحان لنوعين مختلفين من التوزيعات الاحتمالية المتماثلة، وهما التوزيع الطبيعي والتوزيع الموحد، لأن لهما نفس عدد القيم على يسار ويمين المتوسط.

من ناحية أخرى، يمكن أن يكون التوزيع أيضًا متماثلًا وثنائيًا، أي أن يكون له وضعين. ننظر إلى المثال التالي:

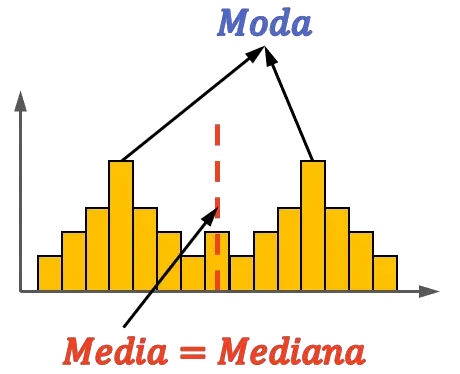
كما ترون في هذا المثال الآخر، يمكن أن يكون التوزيع الثنائي متماثلًا أيضًا، لأنه يمكن أن يحتوي على المتوسط والوسيط في المركز بغض النظر عن القيم الأخرى. ومع ذلك، في هذه الحالة ليس من الضروري أن يكون المنوال مساويًا للمتوسط والمنوال.

أنواع أخرى من التوزيعات حسب تماثلها

إلى جانب التوزيعات المتماثلة، هناك نوعان آخران من التوزيعات غير المتماثلة.

• التوزيع المتماثل : التوزيع له نفس عدد القيم على يسار ويمين الوسط.
• التوزيع المنحرف بشكل إيجابي : يحتوي التوزيع على قيم مختلفة على يمين الوسط أكثر من يساره.
• التوزيع المنحرف سلبيًا : يحتوي التوزيع على قيم مختلفة على يسار الوسط أكثر من القيم الموجودة على يمينه.

كيفية معرفة ما إذا كان التوزيع متماثل

لتحديد ما إذا كان التوزيع متماثلاً أم لا، يجب علينا حساب معامل عدم التماثل بيرسون، وصيغته هي:

ذهب

هو معامل بيرسون،

المتوسط الحسابي،

الوضع (الإحصائيات) و

الانحراف المعياري.

وبالتالي، اعتمادًا على إشارة معامل عدم التماثل بيرسون، سيكون التوزيع متماثلًا أو غير متماثل:

• إذا كان معامل انحراف بيرسون موجبًا، فهذا يعني أن التوزيع منحرف بشكل إيجابي.
• إذا كان معامل انحراف بيرسون سلبيا، فهذا يعني أن التوزيع منحرف سلبا.
• إذا كان معامل بيرسون للانحراف صفراً، فهذا يعني أن التوزيع متماثل.

ومع ذلك، لا يمكن حساب معامل بيرسون إلا إذا كان التوزيع أحادي الواسطة، وإلا فإنه من الضروري استخدام معامل عدم التماثل فيشر، والذي تكون صيغته كما يلي:

ذهب

المتوسط الحسابي،

الانحراف المعياري و

العدد الإجمالي للبيانات.

تفسير معامل عدم تماثل فيشر مطابق لمعامل بيرسون: إذا كان موجبًا يعني أن التوزيع غير متماثل موجبًا، وإذا كان سالبًا يكون التوزيع غير متماثل سالبًا، وإذا كان صفرًا يعني أن التوزيع متماثل.