ما هو التوزيع المفتوح؟

في الإحصاء، التوزيع المفتوح هو توزيع تكراري تكون فيه فئة واحدة أو أكثر (أو “صناديق”) مفتوحة.

على سبيل المثال، يمثل التوزيع التكراري التالي توزيعًا مفتوحًا تكون فيه أصغر فئة مفتوحة:

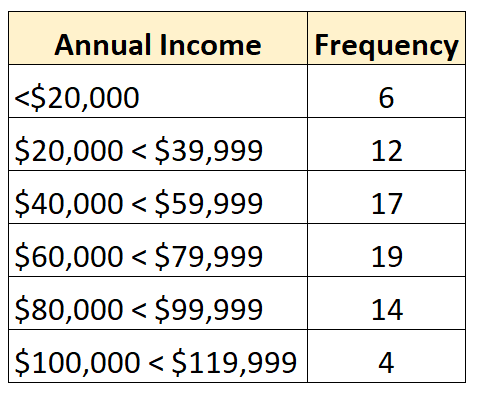
والتوزيع التكراري التالي يوضح التوزيع المفتوح الذي تكون فيه الفئة الأكبر مفتوحة:

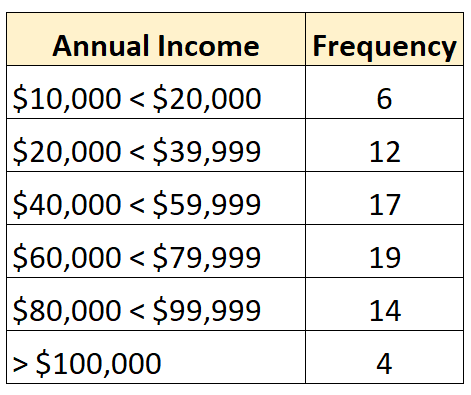
وعلى العكس من ذلك فإن التوزيع المغلق هو التوزيع الذي يكون فيه لكل فئة من التوزيع التكراري حد أعلى وأدنى، كما يلي:

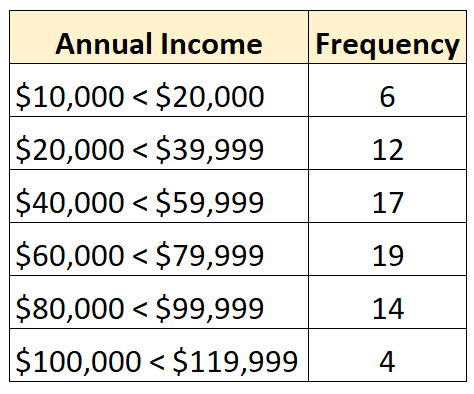
ما الذي يسبب التوزيعات المفتوحة؟

غالبًا ما تكون التوزيعات المفتوحة نتيجة اختيار الباحثين لجمع البيانات بطريقة تجعل أحد الفئات مفتوحًا.

على سبيل المثال، لنفترض أن أحد الباحثين يستطلع آراء سكان مدينة معينة ويسألهم عن دخل أسرهم السنوي.

قد يختار الباحث إعطاء أوسع إجابة ممكنة “> 100000 دولار” لأنه يعلم أن السكان ذوي الدخل المرتفع قد لا يشعرون بالارتياح عند مشاركة المبلغ الذي يكسبونه إذا كان أكبر بكثير من 100000 دولار.

وعلى العكس من ذلك، قد يختار الباحث إعطاء أقصر إجابة ممكنة لأنه يعلم أن السكان الذين يكسبون القليل جدًا لن يشعروا بالارتياح أيضًا لتقاسم ما يكسبونه قليلاً.

باختصار، غالبًا ما يقوم الباحثون بتضمين دورات مفتوحة في استطلاعاتهم لأنهم يريدون زيادة عدد الأشخاص الذين يشعرون بالراحة في الإجابة على أسئلة الاستطلاع.

مشكلة التوزيعات المفتوحة

ومشكلة التوزيعات المفتوحة هي أن البيانات الحقيقية تخضع للرقابة . بمعنى آخر، يمكننا معرفة عدد الأشخاص الذين يكسبون أكثر من 100 ألف دولار في مدينة معينة، لكننا لا نعرف فعليًا دخلهم السنوي بالضبط.

من الممكن أن يكسب بعض الأشخاص 150 ألف دولار، أو 250 ألف دولار، أو 500 ألف دولار أو أكثر، ولكن ليس لدينا أي فكرة لأن كل واحد من هؤلاء الأشخاص لا يمكنه الإشارة إلى أنه يكسب “> 100000 دولار” في “التحقيق”.

نظرًا لأن البيانات تخضع للرقابة في التوزيعات المفتوحة، فإننا غير قادرين أيضًا على حساب المتوسط الدقيق والانحراف المعياري للقيم في مجموعة البيانات نظرًا لأنه لا يمكننا الوصول إلى جميع القيم الموجودة في البيانات الأولية.

كيفية تحليل التوزيع المفتوح

نظرًا لأننا لا نستطيع حساب المتوسط الدقيق للتوزيع المفتوح، فغالبًا ما نستخدم الوسيط كمقياس لـ “مركز” مجموعة البيانات.

تذكر أن الوسيط يمثل القيمة الوسطى لمجموعة البيانات.

عند العمل مع التوزيعات المفتوحة، يمكننا استخدام الصيغة التالية للعثور على أفضل تقدير للوسيط:

أفضل تقدير للوسيط: L + ((n/2 – F) / f) * w

ذهب:

• L: الحد الأدنى للمجموعة الوسطى
• n: العدد الإجمالي للملاحظات
• F: التكرار التراكمي حتى المجموعة الوسطى
• f: تردد المجموعة الوسطى
• w: عرض المجموعة الوسطى

على سبيل المثال، لنفترض أن لدينا التوزيع المفتوح التالي:

يوجد إجمالي 72 قيمة في مجموعة البيانات. لذلك، نحن نعلم أن القيمة المتوسطة ستكون بين القيمتين 36 و37 الأكبر في مجموعة البيانات. تقع كل من هذه القيم في فئة “60.000 دولار – 79.999 دولارًا”، لذلك نعرف أن متوسط الدخل يقع في هذا النطاق.

أفضل تقدير لدينا للوسيط هو:

المتوسط: 60,000 + ((72/2 – 25) / 19) * 19,999 = 71,578 دولارًا

تمثل هذه القيمة أفضل تقدير لدينا لمتوسط الدخل السنوي للأفراد في مجموعة البيانات هذه.