التوزيع الهندسي الزائد

By دكتور بنيامين أندرسون زومار 6, 2023 احتمالا 0 Comments

نوضح في هذه المقالة ما هو التوزيع الهندسي الفائق وكيف يتم حساب الاحتمالية مع هذا النوع من التوزيع. ستجد على الإنترنت صيغة التوزيع الهندسي الزائد، وخصائصه، بالإضافة إلى آلة حاسبة لحساب احتمالية التوزيع الهندسي الزائد.

ما هو التوزيع الهندسي الزائد؟

التوزيع الهندسي الفائق هو توزيع احتمالي يصف عدد الحالات الناجحة في الاستخراج العشوائي دون استبدال عناصر n من السكان.

أي أنه يتم استخدام التوزيع الهندسي الفائق لحساب احتمالية الحصول على نجاحات x عند استخراج عناصر n من المجتمع دون استبدال أي منها.

يحتوي التوزيع الهندسي الفائق على ثلاث معلمات:

N : هو عدد العناصر في المجتمع (N = 0، 1، 2،…).
K : هو الحد الأقصى لعدد حالات النجاح (K = 0، 1، 2،…،N). نظرًا لأنه في التوزيع الهندسي الفائق، لا يمكن اعتبار العنصر إلا “نجاحًا” أو “فشلًا”، فإن NK هو الحد الأقصى لعدد حالات الفشل.
n : هو عدد عمليات جلب عدم الاستبدال التي يتم تنفيذها.

$X \sim HG(N,K,n)$

على سبيل المثال، يتم تعريف المتغير العشوائي المنفصل X الذي له توزيع هندسي مفرط مع المعلمات N=8 وK=5 وn=3 على النحو التالي:

$X \sim HG(8,5,3)$

صيغة التوزيع الهندسي الزائد

صيغة التوزيع الهندسي الزائد هي حاصل ضرب العدد التوافقي لـ K على x في العدد التوافقي لـ NK على nx مقسومًا على العدد التوافقي لـ N على n .

حيث N هو حجم السكان، وK هو العدد الإجمالي للحالات المواتية، وn هو عدد عمليات الاستخراج دون استبدال و x هو عدد الحالات المواتية التي يجب حساب احتمالية حدوثها.

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب احتمال وقوع حدث لمتغير يتبع التوزيع الهندسي الزائد.

مثال على التوزيع الهندسي الزائد

بعد أن رأينا تعريف وصيغة التوزيع الهندسي الزائد، سنحل الآن مثالًا خطوة بخطوة حتى تعرف كيفية حساب احتمال التوزيع الهندسي الزائد.

في كيس نضع 20 كرة زرقاء و30 كرة حمراء، أي أن هناك 50 كرة إجمالاً داخل الكيس. إذا سحبنا ١٢ كرة دون استبدال أي منها، فأوجد احتمال سحب ٤ كرات زرقاء.

أول شيء يتعين علينا القيام به لحل التمرين هو تحديد معلمات التوزيع الهندسي الزائد. في هذه الحالة، إجمالي عدد العناصر في المجتمع هو 50 ( N = 50)، والحد الأقصى لعدد الحالات المواتية هو 20 ( K = 20)، ويتم سحب 12 كرة ( n = 12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

نريد حساب احتمالية سحب 4 كرات زرقاء ( x =4)، لذلك نطبق صيغة التوزيع الهندسي الزائد، ونستبدل المتغيرات بالقيم المقابلة لها ونجري العملية الحسابية:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

حاسبة التوزيع الهندسي الزائد

أدخل معلمات التوزيع الهندسي الفائق في الآلة الحاسبة الإلكترونية التالية لحساب احتمالية حدوث الحدث المطلوب.

تذكر أن N هو حجم السكان، وK هو العدد الإجمالي للحالات المفضلة، و n هو حجم العينة، و x هي القيمة التي نريد إيجاد احتمال حدوث ذلك لها.

خصائص التوزيع الهندسي الزائد

يحتوي التوزيع الهندسي الفائق على الخصائص التالية:

القيمة المتوقعة للتوزيع الهندسي الزائد تساوي عدد العناصر في العينة مضروبًا في إجمالي عدد الحالات المفضلة مقسومًا على عدد العناصر في المجتمع.

$E[X]=\cfrac{n\cdot K}{N}$

نمط التوزيع الهندسي الزائد هو القيمة المقربة للأسفل من حاصل ضرب n+1 في K+1 مقسومًا على N+2 .

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

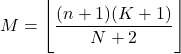
يمكن الحصول على تباين التوزيع الهندسي الزائد باستخدام التعبير التالي:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

دالة توليد اللحظة للتوزيع الهندسي الفائق هي كما يلي:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

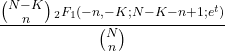
الوظيفة المميزة للتوزيع الهندسي الفائق هي كما يلي:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

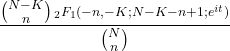
يمكن حساب احتمالية حدوث عدد معين من الأحداث من احتمالية الرقم السابق باستخدام التكرار للتوزيع الهندسي الفائق:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

التوزيع الهندسي الزائد والتوزيع ذو الحدين

الفرق بين التوزيع الهندسي الزائد والتوزيع ذي الحدين هو الاستبدال. يتم استخدام التوزيع الهندسي الزائد عندما لا يتم استبدال عمليات الاسترجاع، ومع ذلك، في عمليات استرجاع التوزيع ذي الحدين يتم استبدالها.

على سبيل المثال، إذا قمنا بسحب خمس بطاقات بشكل عشوائي في المجموعة وأردنا حساب احتمال الحصول على بطاقة معينة، وإذا لم نستبدل كل بطاقة نرسمها، فيجب علينا استخدام التوزيع الهندسي الزائد لإجراء الحساب. ولكن إذا قمنا بإعادتها عند إزالة البطاقة قبل إجراء الاستخراج التالي، فيجب علينا استخدام التوزيع ذي الحدين لحساب الاحتمال.

عندما يكون الرقم N كبيرًا، تكون النسبة n/N صغيرة وعدد الحالات المفضلة المرغوبة صغير جدًا، يمكننا استخدام التوزيع الهندسي الفائق كتقريب للتوزيع ذي الحدين. ومع ذلك، لا أوصي به لأن النتيجة لن تكون موثوقة، علاوة على ذلك، من الأسهل حساب الاحتمالات باستخدام قانون ذي الحدين مقارنة بقانون الهندسة الفائقة.

About Author

دكتور بنيامين أندرسون

مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر