التوزيع بتكرار
تشرح هذه المقالة ما هي التوزيعات التكرارية وكيفية تحقيقها. ستجد أيضًا أمثلة خطوة بخطوة للتوزيعات التكرارية، وبالإضافة إلى ذلك، ستتمكن من التدرب على التمارين التي تم حلها.
ما هو توزيع التردد؟
في الإحصاء، التوزيع التكراري هو جدول يتم فيه تجميع القيم المختلفة للعينة في صفوف وفي كل عمود يتم عرض نوع التكرار لكل قيمة. لذلك، يتم استخدام التوزيع التكراري لإظهار جميع أنواع الترددات في مجموعة البيانات.
وبشكل أكثر تحديدًا، يتضمن التوزيع التكراري التكرار المطلق والتكرار المطلق التراكمي والتكرار النسبي والتكرار النسبي التراكمي.
ومن خصائص التوزيعات التكرارية أنها مفيدة جداً في تلخيص عينة إحصائية لمتغير كمي ومتغير نوعي.
كيفية جعل توزيع التردد
لإجراء التوزيع التكراري، يجب عليك اتباع الخطوات التالية:
- قم بتنظيم البيانات في فئات مختلفة وقم بإنشاء جدول يتوافق فيه كل صف مع فئة ما.
- احسب التكرار المطلق لكل فئة في العمود الثاني من الجدول.
- احسب التكرار المطلق التراكمي لكل فئة في العمود الثالث من الجدول.
- احسب التكرار النسبي لكل فئة في العمود الرابع من الجدول.
- احسب التكرار النسبي التراكمي لكل فئة في العمود الخامس من الجدول.
- اختياريًا، يمكن إضافة عمودين يتم فيهما حساب التكرار النسبي والتكرار النسبي التراكمي كنسبة مئوية، ولهذا تحتاج ببساطة إلى ضرب كلا العمودين في 100.
مثال لتوزيع التردد
بمجرد أن رأينا تعريف التوزيع التكراري والنظرية حول كيفية بنائه، في هذا القسم يتم حل مثال خطوة بخطوة.
- الدرجات التي تم الحصول عليها في مادة الإحصاء في فصل مكون من 30 طالبا هي كما يلي. بناء توزيع ترددي لمجموعة البيانات.
![]()
![]()
![]()
بما أن جميع الأرقام يمكن أن تكون أعدادًا صحيحة فقط، فهي متغير منفصل. ولذلك ليس من الضروري تجميع البيانات في فترات.
لذا، لإجراء توزيع تكراري، نحتاج إلى إنشاء جدول تكون فيه كل قيمة مختلفة صفًا، ثم نحتاج إلى إيجاد التكرار المطلق لكل قيمة:

لاحظ أن مجموع كل التكرارات المطلقة يساوي إجمالي عدد البيانات. إذا لم يتم احترام هذه القاعدة، فهذا يعني أنك نسيت تقديم معلومات معينة.
والآن بعد أن عرفنا التكرار المطلق، علينا حساب التكرار المطلق التراكمي. في هذا الحساب لدينا خياران: إما أن نضيف التكرار المطلق للقيمة بالإضافة إلى جميع التكرارات المطلقة للقيم الأصغر، أو على العكس من ذلك، نضيف التكرار المطلق للقيمة بالإضافة إلى التكرار المطلق التراكمي للقيمة السابقة.

يتوافق التكرار المطلق التراكمي للقيمة الأخيرة دائمًا مع إجمالي عدد البيانات، ويمكنك استخدام هذه الخدعة للتحقق من صحة الحسابات.
بعد ذلك، نحتاج إلى تحديد التكرار النسبي، والذي يتم حسابه عن طريق قسمة التكرار المطلق على إجمالي عدد نقاط البيانات (30):

ضع في اعتبارك أن مجموع جميع الترددات النسبية يساوي دائمًا 1، وإلا فهذا يعني أن حسابًا معينًا للتوزيع التكراري خاطئ.
وأخيرًا، نحتاج فقط إلى استخراج التكرار النسبي التراكمي. للقيام بذلك، يجب عليك إضافة التكرار النسبي للقيمة المعنية بالإضافة إلى جميع التكرارات النسبية السابقة أو، والتي تصل إلى نفس الشيء، التكرار النسبي المتراكم السابق:

وباختصار فإن التوزيع التكراري لجميع ترددات بيانات المشكلة هو كما يلي:

توزيع التردد للبيانات المجمعة
لإجراء توزيع تكراري للبيانات المجمعة في فترات ، فإن الاختلاف الوحيد هو أنه يجب أولاً تجميع مجموعة البيانات في فترات مختلفة، ولكن تتم بقية الحسابات بنفس الطريقة كما في التوزيع التكراري دون تجميع البيانات.
على سبيل المثال، تم حل مشكلة إنشاء التوزيع التكراري للبيانات المجمعة أدناه.
- تم قياس طول 20 شخصًا وتم الحصول على النتائج المذكورة أدناه. إنشاء توزيع تكراري عن طريق فصل البيانات إلى فترات.
![]()
![]()
تتبع البيانات الموجودة في هذه العينة توزيعًا مستمرًا، حيث يمكن أن تكون الأرقام عشرية وبالتالي يمكن أن تأخذ أي قيمة. لذلك، سنقوم بالتوزيع التكراري بتجميع البيانات في فترات.
على الرغم من وجود العديد من القواعد الرياضية لإنشاء فترات زمنية للعينة، إلا أننا في هذه الحالة سنقوم ببساطة بإنشاء فترات زمنية بعرض 10 أعشار.
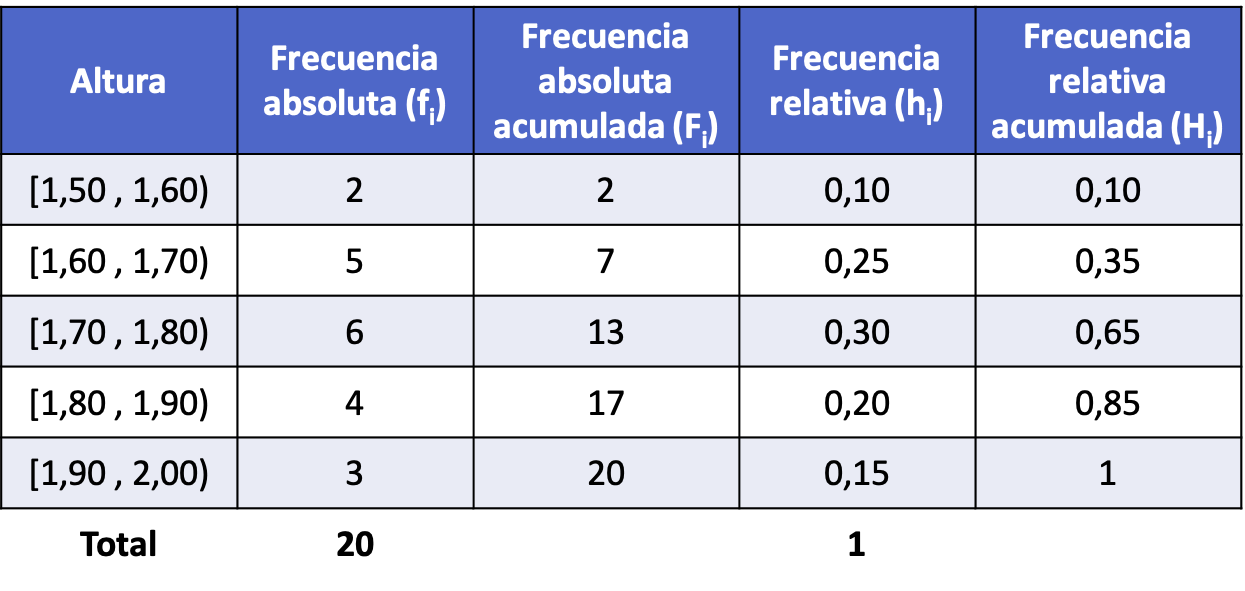
لذلك، بعد حساب جميع أنواع الترددات لكل فاصل زمني (الإجراء هو نفسه كما في المثال أعلاه)، يكون توزيع التكرار مع البيانات المجمعة في فترات كما يلي:
حل تمارين التوزيع التكراري
التمرين 1
سألنا 20 شخصًا عن عدد المرات التي يذهبون فيها إلى السينما شهريًا، وإليكم النتائج:
![]()
![]()
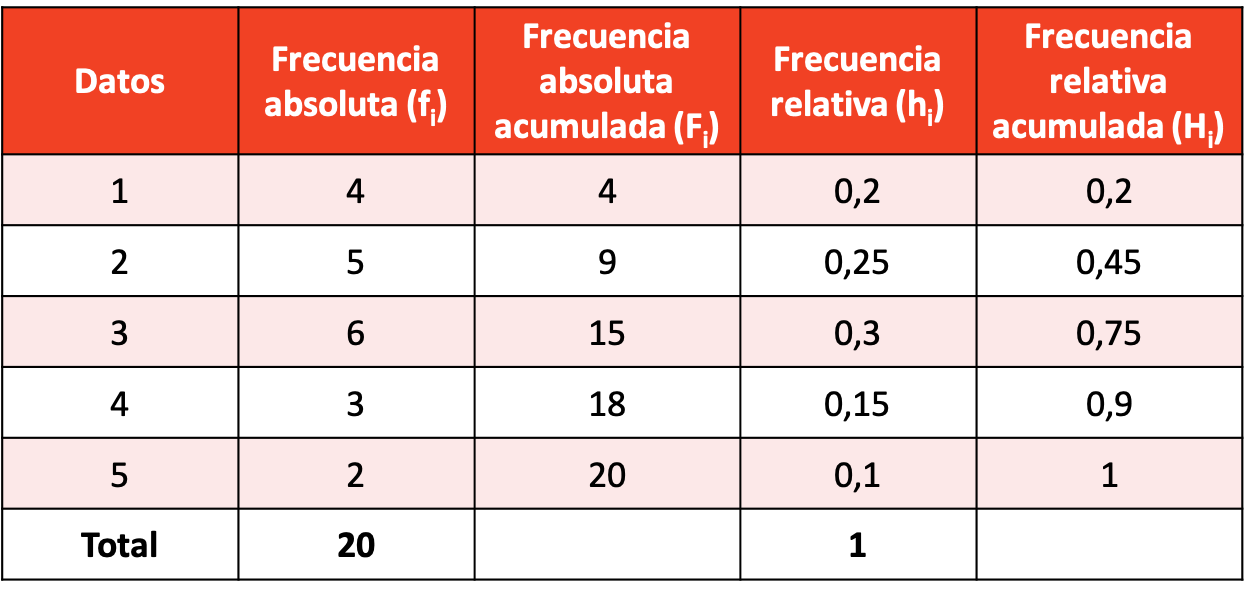
قم بإجراء توزيع ترددي باستخدام عينة البيانات الناتجة.
توزيع الترددات مع حسابات جميع أنواع الترددات هو كما يلي:
تمرين 2
ترغب في إجراء دراسة إحصائية عن وزن العاملين في شركة بها 36 موظفًا. وفيما يلي أوزان العمال معبرا عنها بالكيلوغرام:
![]()
![]()
![]()
![]()
![]()
![]()
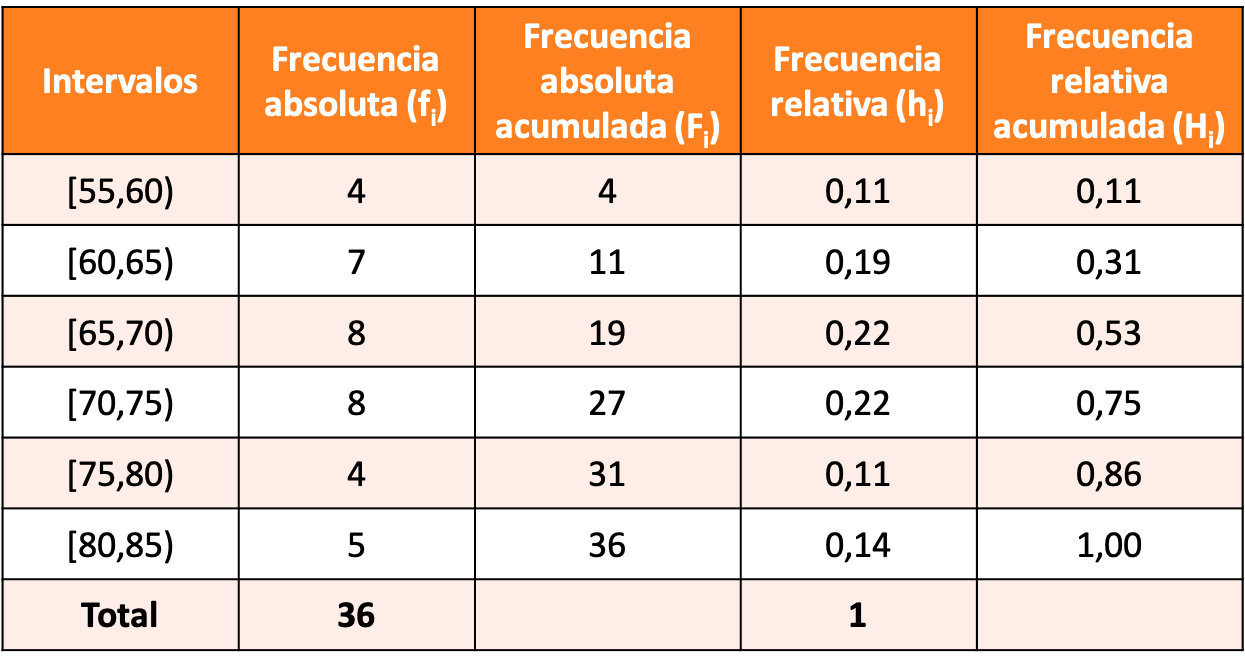
أنشئ توزيعًا تكراريًا للبيانات المجمعة من خلال عمل فترات من 5 وحدات، وليكن الفاصل الأول [55،60).
حل التمرين هو التوزيع التكراري التالي: