Socs: اختصار مفيد لوصف التوزيعات

في الإحصاء، غالبًا ما نريد أن نفهم كيفية توزيع مجموعة من البيانات. وعلى وجه الخصوص، هناك أربعة أشياء من المفيد معرفتها حول التوزيع:

1 . شكل

• هل التوزيع متماثل أم منحرف إلى جانب واحد؟
• هل التوزيع أحادي النسق (ذروة واحدة) أم ثنائي النسق (قمتان)؟

2. القيم المتطرفة

• هل هناك أي قيم متطرفة موجودة في التوزيع؟

3. المركز

• ما هو المتوسط والوسيط وطريقة التوزيع؟

4.الانتشار

• ما هو المدى والمدى الربيعي والانحراف المعياري والتباين للتوزيع؟

SOCS هو اختصار مفيد يمكننا استخدامه لتذكر هذه الأشياء الأربعة. وتعني “الشكل، القيم المتطرفة، المركز، الانتشار”.

دعونا نستعرض مثالًا بسيطًا لكيفية استخدام SOCS لوصف التوزيع.

مثال: كيفية استخدام SOCS لوصف التوزيع

لنفترض أن لدينا مجموعة البيانات التالية التي توضح ارتفاع عينة مكونة من 20 نباتًا مختلفًا.

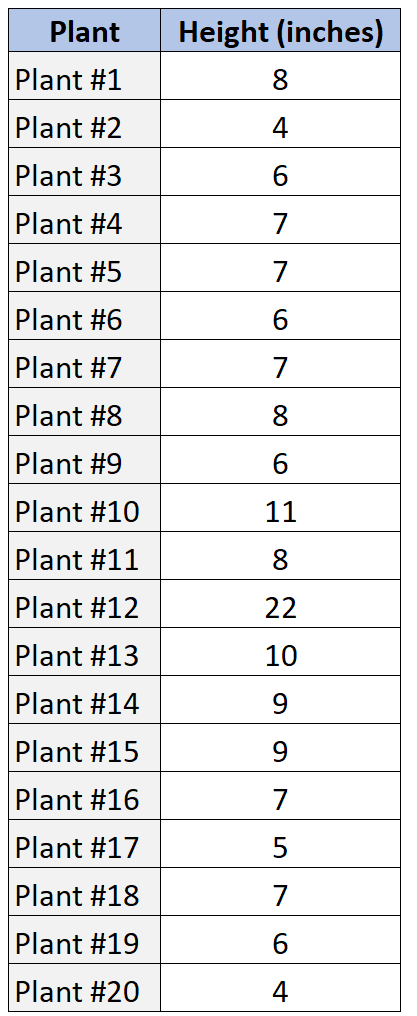
وإليك كيف يمكننا استخدام SOCS لوصف هذا التوزيع لقيم البيانات.

شكل

أولا، نريد أن نصف شكل التوزيع.

إحدى الطرق المفيدة لتصور شكل التوزيع هي إنشاء رسم بياني يعرض تكرارات كل قيمة في مجموعة البيانات:

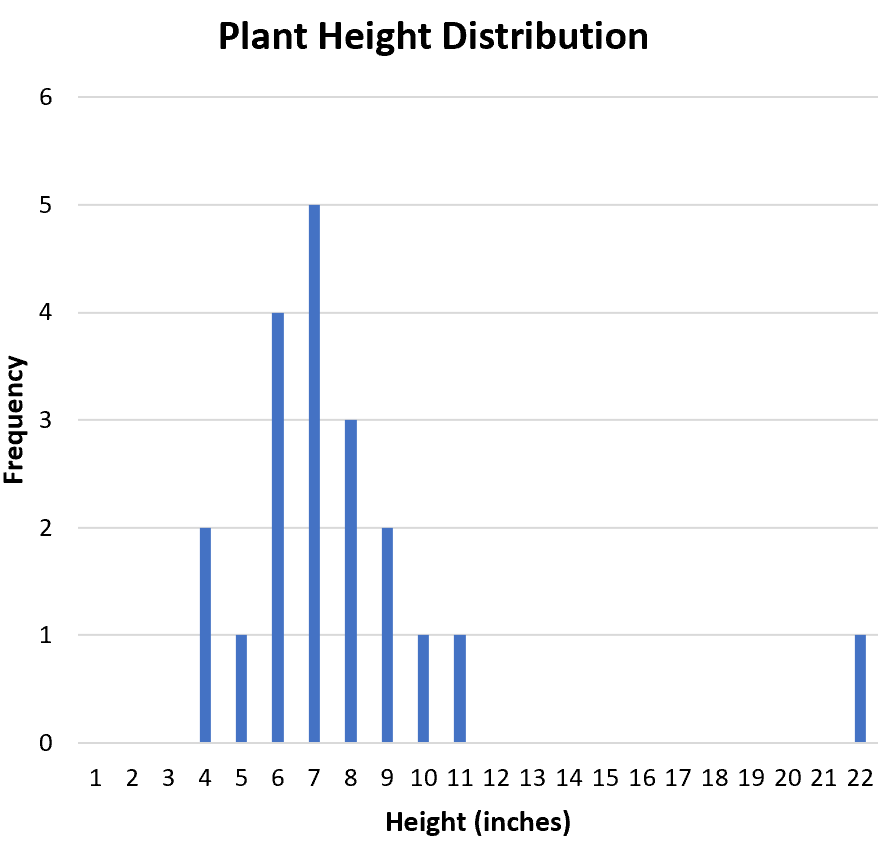
هل التوزيع متماثل أم منحرف إلى جانب واحد؟   من الرسم البياني يمكننا أن نرى أن التوزيع متماثل تقريبًا. بمعنى آخر، القيم ليست متحيزة بطريقة أو بأخرى.

هل التوزيع أحادي النسق (ذروة واحدة) أم ثنائي النسق (قمتان)؟ التوزيع أحادي. ويبلغ ذروته عند القيمة “7”.

القيم المتطرفة

بعد ذلك، نريد تحديد ما إذا كان هناك أي قيم متطرفة في مجموعة البيانات. من الرسم البياني يمكننا فحص التوزيع بصريًا ونرى أن 22 من المحتمل أن تكون قيمة متطرفة:

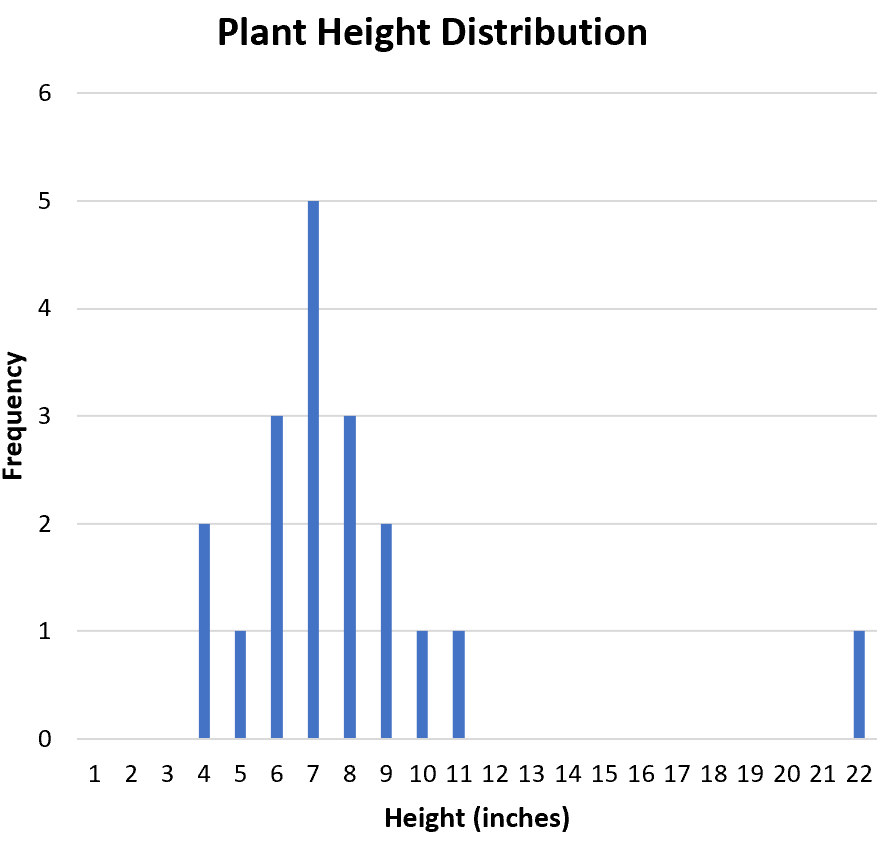
هناك طريقة شائعة لتعريف القيمة المتطرفة بشكل رسمي وهي أي قيمة تكون 1.5 مرة من النطاق الربيعي أعلى من الربع الثالث أو أقل من الربع الأول.

باستخدام حاسبة المدى الربيعي، يمكننا إدخال 20 قيمة من البيانات الأولية ونرى أن الربيع الثالث هو 9 ، والمدى الربيعي هو 3 ، وبالتالي فإن أي قيمة أكبر من 9 + (1.5*3) = 13.5 هي قيمة متطرفة، حسب التعريف.

بما أن 22 أكبر من 13.5، فيمكننا أن نعلن أن 22 قيمة متطرفة.

مركز

نريد بعد ذلك وصف مكان مركز التوزيع. ثلاثة مقاييس شائعة للاتجاه المركزي يمكننا استخدامها هي المتوسط والوسيط والمنوال.

المتوسط: هذا هو متوسط قيمة التوزيع. ونجد ذلك عن طريق جمع كافة القيم الفردية ثم قسمتها على إجمالي عدد القيم:

المتوسط = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7.85

الوسيط: هذه هي القيمة “المتوسطة” للتوزيع. ونجد ذلك من خلال ترتيب جميع القيم من الأصغر إلى الأكبر ومن ثم تحديد القيمة المتوسطة. اتضح أن 7 .

4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22

الوضع: هذه هي القيمة التي تظهر بشكل متكرر. اتضح أن 7 .

الانتشار

بعد ذلك، نريد وصف توزيع القيم في التوزيع. أربعة مقاييس شائعة للتشتت يمكننا استخدامها هي المدى، والمدى الرباعي، والانحراف المعياري، والتباين.

النطاق: هذا هو الفرق بين أكبر وأصغر قيمة في مجموعة البيانات. ويتبين أن هذا هو 22 – 4 = 18 .

النطاق الرباعي: يقيس عرض الـ 50% الوسطى من قيم البيانات. بإدخال 20 قيمة من البيانات الأولية في حاسبة النطاق الربيعي، يمكننا أن نرى أن هذا يساوي 3 .

الانحراف المعياري: هذا مقياس لمتوسط توزيع قيم البيانات. وبإدخال 20 قيمة من البيانات الأولية في حاسبة التباين والانحراف المعياري، يمكننا أن نرى أن الانحراف المعياري يساوي 3.69 .

التباين: هذا هو ببساطة الانحراف المعياري، مربع. وهذا يساوي 3.69 ² = 13.63 .

خاتمة

باستخدام SOCS كدليل، تمكنا من وصف توزيع ارتفاع النبات على النحو التالي:

• كان التوزيع أحاديًا ومتماثلًا، مما يعني أنه كان له قمة واحدة فقط ولم يكن منحرفًا إلى جانب أو آخر.
• كان للتوزيع قيمة متطرفة واحدة: 22.
• كان للتوزيع متوسط 7.85، ووسيط 7، وطريقة 7.
• كان للتوزيع مدى قدره 18، ومدى ربعي قدره 3، وانحراف معياري قدره 3.69، وتباين قدره 13.63.

لاحظ أنه يمكننا استخدام SOCS لوصف أي توزيع، وهي طريقة مفيدة بالنسبة لنا لفهم شكل التوزيع بشكل كامل، وما إذا كان يحتوي على قيم متطرفة، ومكان المركز تقريبًا، وكيفية توزيع قيم البيانات. نكون.