كيفية إنشاء غابات عشوائية في r (خطوة بخطوة)

عندما تكون العلاقة بين مجموعة من المتغيرات المتوقعة ومتغير الاستجابة معقدة للغاية، فإننا غالبًا ما نستخدم أساليب غير خطية لنمذجة العلاقة بينهما.

إحدى هذه الطرق هي بناء شجرة القرار . ومع ذلك، فإن الجانب السلبي لاستخدام شجرة قرار واحدة هو أنها تميل إلى المعاناة من التباين العالي .

أي أننا إذا قسمنا مجموعة البيانات إلى نصفين وقمنا بتطبيق شجرة القرار على كلا النصفين، فقد تكون النتائج مختلفة تمامًا.

إحدى الطرق التي يمكننا استخدامها لتقليل التباين في شجرة قرار واحدة هي بناء نموذج غابة عشوائي ، والذي يعمل على النحو التالي:

1. خذ عينات تمهيدية من مجموعة البيانات الأصلية.

2. قم بإنشاء شجرة قرارات لكل عينة تمهيدية.

• عند إنشاء الشجرة، في كل مرة يتم فيها أخذ الانقسام بعين الاعتبار، تعتبر عينة عشوائية فقط من المتنبئين m مرشحين للانقسام من المجموعة الكاملة للمتنبئين p . بشكل عام، نختار m يساوي √p .

3. متوسط التوقعات من كل شجرة للحصول على النموذج النهائي.

وقد تبين أن الغابات العشوائية تميل إلى إنتاج نماذج أكثر دقة من أشجار القرار الواحد وحتى النماذج المعبأة .

يوفر هذا البرنامج التعليمي مثالاً خطوة بخطوة حول كيفية إنشاء نموذج غابة عشوائي لمجموعة بيانات في R.

الخطوة 1: تحميل الحزم اللازمة

أولاً، سنقوم بتحميل الحزم اللازمة لهذا المثال. في هذا المثال البسيط، نحتاج إلى حزمة واحدة فقط:

 library (randomForest)

الخطوة 2: ضبط نموذج الغابة العشوائية

في هذا المثال، سوف نستخدم مجموعة بيانات R مدمجة تسمى جودة الهواء والتي تحتوي على قياسات لجودة الهواء في مدينة نيويورك على مدار 153 يومًا فرديًا.

 #view structure of air quality dataset
str(airquality)

'data.frame': 153 obs. of 6 variables:
 $ Ozone: int 41 36 12 18 NA 28 23 19 8 NA ...
 $Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
 $ Wind: num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
 $ Temp: int 67 72 74 62 56 66 65 59 61 69 ...
 $Month: int 5 5 5 5 5 5 5 5 5 5 ...
 $Day: int 1 2 3 4 5 6 7 8 9 10 ...

#find number of rows with missing values
sum(! complete . cases (airquality))

[1] 42

تحتوي مجموعة البيانات هذه على 42 صفًا بقيم مفقودة. لذلك، قبل تركيب نموذج الغابة العشوائي، سنقوم بملء القيم المفقودة في كل عمود بمتوسطات العمود:

 #replace NAs with column medians
for (i in 1: ncol (air quality)) {
  airquality[,i][ is . na (airquality[, i])] <- median (airquality[, i], na . rm = TRUE )
}

ذات صلة: كيفية احتساب القيم المفقودة في R

يوضح التعليمة البرمجية التالية كيفية ملاءمة نموذج الغابة العشوائي في R باستخدام وظيفة RandomForest() من حزمة RandomForest .

 #make this example reproducible
set.seed(1)

#fit the random forest model
model <- randomForest(
  formula = Ozone ~ .,
  data = airquality
)

#display fitted model
model

Call:
 randomForest(formula = Ozone ~ ., data = airquality) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 327.0914
                    % Var explained: 61

#find number of trees that produce lowest test MSE
which.min(model$mse)

[1] 82

#find RMSE of best model
sqrt(model$mse[ which . min (model$mse)]) 

[1] 17.64392

من النتيجة يمكننا أن نرى أن النموذج الذي أنتج أدنى اختبار لمتوسط مربع الخطأ (MSE) استخدم 82 شجرة.

يمكننا أيضًا أن نرى أن جذر متوسط مربع الخطأ لهذا النموذج كان 17.64392 . يمكننا أن نفكر في هذا باعتباره متوسط الفرق بين القيمة المتوقعة للأوزون والقيمة الفعلية المرصودة.

يمكننا أيضًا استخدام الكود التالي لإنتاج قطعة أرض لاختبار MSE بناءً على عدد الأشجار المستخدمة:

 #plot the MSE test by number of trees
plot(model)

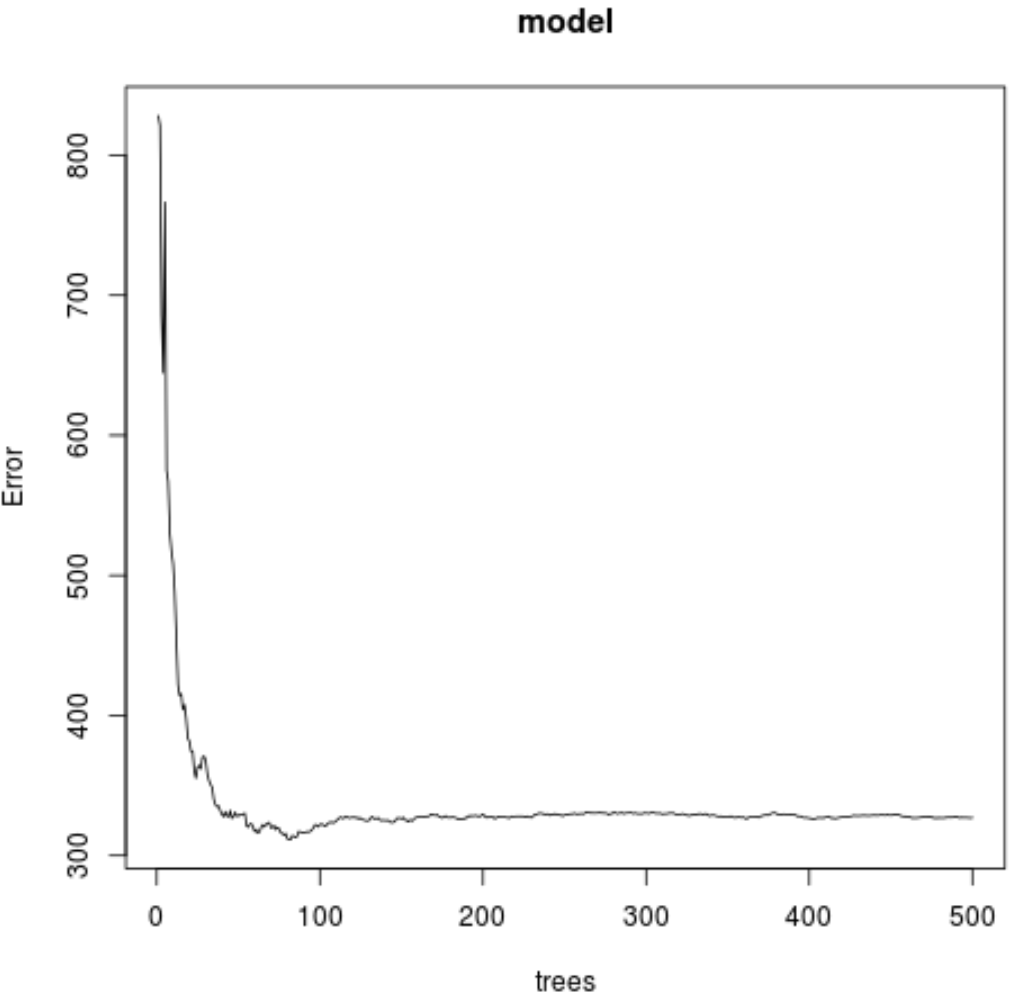
ويمكننا استخدام الدالة varImpPlot() لإنشاء مخطط يعرض أهمية كل متغير متنبئ في النموذج النهائي:

 #produce variable importance plot
varImpPlot(model) 

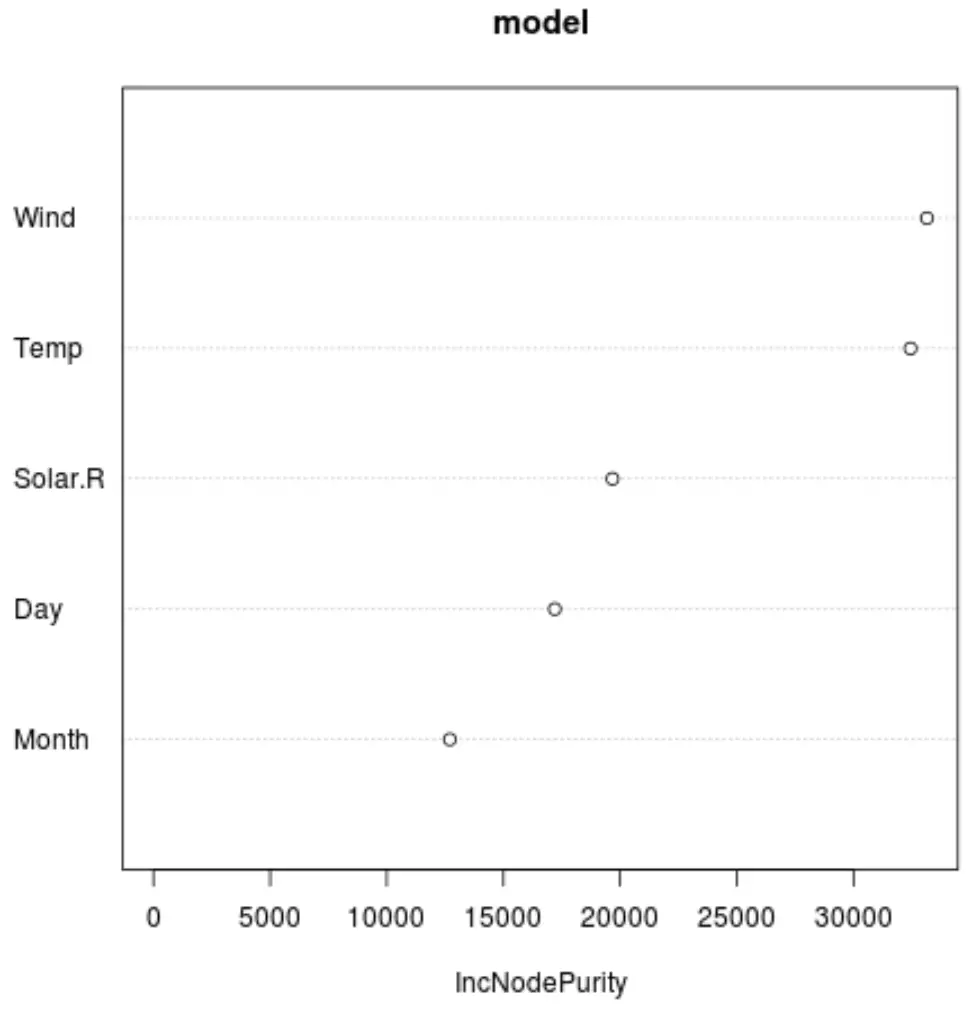
يعرض المحور السيني متوسط الزيادة في نقاء العقدة لأشجار الانحدار كدالة للتقسيم عبر المتنبئين المختلفين المعروضين على المحور الصادي.

من الرسم البياني، يمكننا أن نرى أن الرياح هي المتغير الأكثر أهمية، تليها درجة الحرارة .

الخطوة 3: ضبط النموذج

افتراضيًا، تستخدم الدالة RandomForest() 500 شجرة و(إجمالي المتنبئين/3) تنبؤات تم اختيارها عشوائيًا كمرشحين محتملين لكل تقسيم. يمكننا ضبط هذه المعلمات باستخدام وظيفة tuneRF() .

يوضح الكود التالي كيفية العثور على النموذج الأمثل باستخدام المواصفات التالية:

• ntreeTry: عدد الأشجار المراد بناءها.
• mtryStart: العدد الأولي لمتغيرات التوقع التي يجب مراعاتها في كل قسم.
• عامل الخطوة: عامل للزيادة حتى يتوقف الخطأ المقدر خارج الحقيبة عن التحسن بمقدار معين.
• التحسين: المقدار الذي يجب تحسين خطأ خروج الكيس به لمواصلة زيادة عامل الخطوة.

 model_tuned <- tuneRF(
               x=airquality[,-1], #define predictor variables
               y=airquality$Ozone, #define response variable
               ntreeTry= 500 ,
               mtryStart= 4 , 
               stepFactor= 1.5 ,
               improve= 0.01 ,
               trace= FALSE #don't show real-time progress
               )

تنتج هذه الوظيفة المخطط التالي، الذي يعرض عدد المتنبئات المستخدمة عند كل تقسيم عند إنشاء الأشجار على المحور السيني والخطأ المقدر خارج الحقيبة على المحور الصادي:

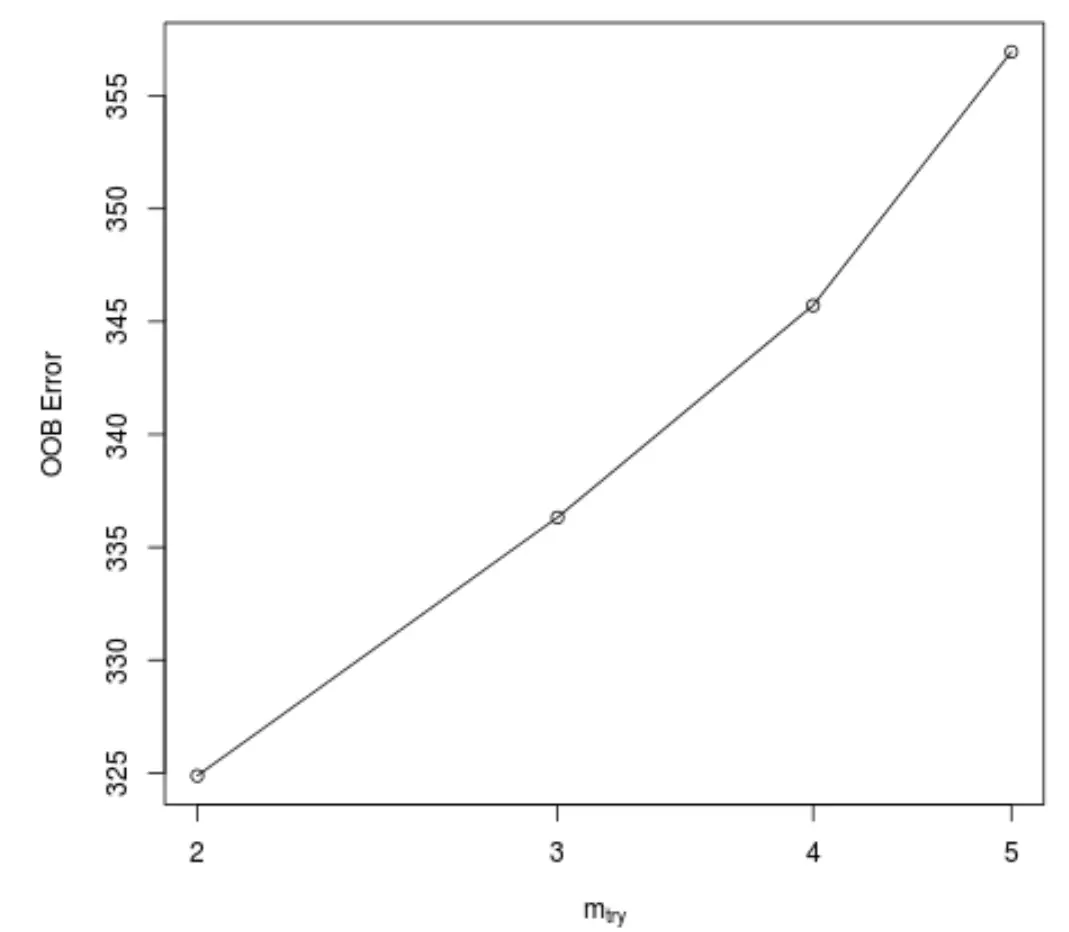
يمكننا أن نرى أنه تم الحصول على أقل خطأ في OOB باستخدام اثنين من المتنبئين الذين تم اختيارهم عشوائيًا عند كل تقسيم عند بناء الأشجار.

يتوافق هذا في الواقع مع الإعداد الافتراضي (إجمالي المتنبئين/3 = 6/3 = 2) الذي تستخدمه الدالة RandomForest() الأولية.

الخطوة 4: استخدم النموذج النهائي لعمل تنبؤات

وأخيرًا، يمكننا استخدام نموذج الغابة العشوائية المعدلة للتنبؤ بالملاحظات الجديدة.

 #define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)

#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)

27.19442

وبناء على قيم المتغيرات التنبؤية، يتوقع نموذج الغابة العشوائية المجهزة أن قيمة الأوزون ستكون 27.19442 في هذا اليوم بالذات.

يمكن العثور على رمز R الكامل المستخدم في هذا المثال هنا .