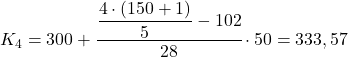الخماسيات (إحصائيات)

في هذه المقالة نوضح ما هي الخماسيات وكيف يتم حسابها. ستجد العديد من الأمثلة المحلولة لحساب الخُمس، وبالإضافة إلى ذلك، ستتمكن من حساب الخُمس لأي عينة إحصائية باستخدام الآلة الحاسبة عبر الإنترنت.

ما هي الخماسيات؟

في الإحصاء، الخماسيات هي أربع قيم تقسم مجموعة البيانات إلى خمسة أجزاء متساوية. وبالتالي فإن الشرائح الخمسية الأولى والثانية والثالثة والرابعة تمثل 20% و40% و60% و80% من بيانات العينة على التوالي.

أي أن قيمة الخُمس الثالث على سبيل المثال أعلى من 60% من جميع البيانات التي تم جمعها، ولكنها أقل من بقية البيانات.

رمز الشرائح الخمسية هو الحرف الكبير K مع مؤشر الشريحة الخمسية، أي أن الشريحة الخمسية الأولى هي K ₁ ، والخميس الثاني هو K ₂ ، والخميس الثالث هو K ₃ ، والخميس الرابع هو K ₄ . على الرغم من أنه يمكن أيضًا تمثيله بالحرف Q (لا يوصى به لأنه يسبب ارتباكًا مع الربعيات).

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب الخُمس لأي مجموعة بيانات.

الخماسيات هي مقياس للوضع غير المركزي إلى جانب الربعيات والعشريات والنسب المئوية. إذا كنت مهتمًا أكثر، يمكنك التحقق مما يعنيه كل نوع من هذه الأنواع الكمية على موقعنا الإلكتروني.

وتجدر الإشارة إلى أن الخُمس قد يكون له تعريف آخر. في الاقتصاد، تمثل الشرائح الخمسية النسبة المئوية للسكان مرتبة حسب الدخل، أو بمعنى آخر، تصنف السكان حسب مستويات الدخل. على سبيل المثال، فإن الشريحة الخمسية الأولى تمثل أفقر 20% من السكان، والشريحة الخمسية الثانية تمثل 40% من السكان ذوي الدخل الأدنى، وهكذا.

كيفية حساب الخماسيات

لحساب موضع الشرائح الخمسية لعينة أو مجتمع إحصائي، يجب عليك ضرب عدد الشرائح الخمسية في مجموع إجمالي عدد البيانات زائد واحد وتقسيم النتيجة على خمسة.

ولذلك، فإن صيغة الخماسيات هي:

يرجى ملاحظة: نتيجة هذه الصيغة تخبرنا بموقع الشريحة الخمسية، وليس قيمتها. وبالتالي فإن الخُمس سيكون البيانات الموجودة في الموضع الذي حصلت عليه الصيغة.

لكن في بعض الأحيان نتيجة هذه الصيغة تعطينا رقما عشريا، لذلك يجب علينا التمييز بين حالتين اعتمادا على ما إذا كانت النتيجة رقما عشريا أم لا:

• إذا كانت نتيجة الصيغة رقمًا بدون جزء عشري ، فإن الشريحة الخمسية هي البيانات الموجودة في الموضع الذي توفره الصيغة أعلاه.
• إذا كانت نتيجة الصيغة رقمًا بجزء عشري ، فسيتم حساب القيمة الخماسية باستخدام التعبير التالي:

حيث x _i و x _i+1 هما أرقام المواضع التي يقع بينها الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى، و d هو الجزء العشري من الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى.

إذا كنت خائفًا عندما رأيت الكثير من الخطوات لتحديد الخماسيات لمجموعة البيانات، فلا تقلق، فالأمر بسيط جدًا في الواقع. اقرأ المثالين التاليين وسوف تفهم بالتأكيد بشكل أفضل.

ملحوظة : لا يزال المجتمع الإحصائي غير متفق تمامًا على كيفية حساب الشرائح الخمسية، لذلك قد تجد كتابًا يشرح الأمر بشكل مختلف قليلاً.

أمثلة على حساب الخماسيات

نترك لك أدناه تمرينين تم حلهما خطوة بخطوة حول كيفية الحصول على الخُمس من سلسلة البيانات. إذن، حتى تتمكن من رؤية الحالتين المحتملتين، في التمرين الأول النتائج ليست عشرية وفي التمرين الثاني تكون كذلك.

مثال 1

• احسب الخماسيات لسلسلة البيانات التالية:

كما رأيت في الشرح أعلاه، فإن صيغة العثور على موضع الشرائح الخمسية هي:

تشير المعلمة n إلى إجمالي عدد البيانات، وهو 49، لذا للعثور على موضع الشريحة الخمسية الأولى نحتاج إلى استبدال n بـ 49 و k بـ 1:

ومن الصيغة حصلنا على الرقم 10، مما يعني أن الشريحة الخمسية تقع في المركز العاشر من القائمة المرتبة، وهو ما يتوافق مع البيانات 205.

لحساب الخُمس الثاني، يجب عليك استخدام نفس الصيغة مع استبدال k بـ 2:

وبالتالي فإن الشريحة الخمسية الثانية تقع في الموضع رقم 20 من القائمة المرتبة، أي القيمة 236.

مرة أخرى، نكرر العملية لتحديد الشريحة الخمسية 3، لكن منطقيًا نستبدل k بـ 3:

وبالتالي فإن الخُمس الثالث هو البيانات الموجودة في الموضع 30، وهو ما يعادل 266.

وأخيرًا، نطبق الصيغة مرة أخرى لحساب الخُمس الرابع:

وبالتالي فإن الخُمس الرابع يقع في الموضع 40، وبالتالي فإن الخُمس الرابع هو 286.

مثال 2

• احسب الخماسيات الأربعة للبيانات الإحصائية المجمعة في الجدول التالي:.

بنفس الطريقة كما في المثال السابق، للحصول على مواضع الشرائح الخمسية، يجب عليك استخدام الصيغة التالية:

في هذه الحالة، يكون حجم العينة 42 ملاحظة، لذا للعثور على موضع الشريحة الخمسية الأولى نحتاج إلى استبدال المعلمة n بـ 42 و k بـ 1:

ومع ذلك، على عكس المثال الأول، هذه المرة تعطينا الصيغة رقمًا عشريًا، لذلك نحتاج إلى تطبيق الصيغة التالية لحساب الخُمس الدقيق:

الرقم الذي تم الحصول عليه من الصيغة الأولى هو 8.6، وبالتالي فإن الخمس الأول يقع بين البيانات الثامنة والتاسعة، وهما 78 و79 على التوالي. لذلك، x _i هو 78، x _i+1 هو 79 و d هو الجزء العشري من الرقم الذي تم الحصول عليه، أي 0.6.

والآن نقوم بنفس الإجراء مرة أخرى لإيجاد الشريحة الخمسية الثانية. نحسب موضعها أولاً:

لكن من الصيغة نحصل على رقم عشري بين 17 و 18 بحيث يكون الخُمس الثاني بين المركزين السابع عشر والثامن عشر، والذي تتوافق قيمه على التوالي مع 109 و 112 من القائمة المرتبة. ولذلك، فإننا نطبق الصيغة الثانية في العملية لتحديد القيمة الخماسية الدقيقة:

نكرر الطريقة للحصول على الخُمس الثالث، نحدد موقعه أولاً:

الرقم المحسوب 25.8 يعني أن القيمة الخماسية ستكون بين المركزين الخامس والعشرين والسادس والعشرين، وقيمتيهما 134 و141. وبالتالي فإن حساب القيمة الخماسية الدقيقة هو:

وأخيرًا، نكرر نفس الإجراء مرة أخيرة لحساب الخُمس 4. ونجد موضعه أولاً:

وبالتالي فإن القيمة الدقيقة للشريحة الخمسية الرابعة ستكون بين 34 و35، والتي تتوافق مواقعها مع البيانات 172 و179. وبالتالي، فإن حساب الشريحة الخمسية الرابعة هو:

حاسبة الخماسية

أدخل مجموعة بيانات إحصائية في الآلة الحاسبة التالية لحساب الخُمس. يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.

الخماسيات في البيانات المجمعة

لحساب الخُمس عندما يتم تجميع البيانات في فواصل زمنية، يجب عليك أولاً العثور على الفاصل الزمني أو الفئة الخاصة بها باستخدام الصيغة التالية:

وبالتالي فإن الخُمس سيكون في الفترة التي يكون تكرارها المطلق أكبر مباشرة من الرقم الذي تم الحصول عليه بالتعبير السابق.

وبمجرد أن نعرف الفترة التي ينتمي إليها الخُمس، يجب علينا تطبيق الصيغة التالية للعثور على القيمة الدقيقة للخُمس:

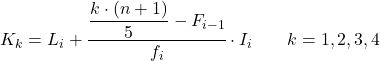
ذهب:

• L _i هو الحد الأدنى للفاصل الزمني الذي يقع فيه الخُمس.
• n هو العدد الإجمالي للملاحظات.
• F _i-1 هو التردد المطلق التراكمي للفاصل الزمني السابق.
• f _i هو التكرار المطلق للفاصل الزمني الذي يقع فيه الخُمس.
• I _i هو عرض الفاصل الزمني الخماسي.

حتى تتمكن من رؤية كيفية القيام بذلك، إليك مثال تم حله لحساب الخُمس لسلسلة البيانات التالية مجمعة في فواصل زمنية:

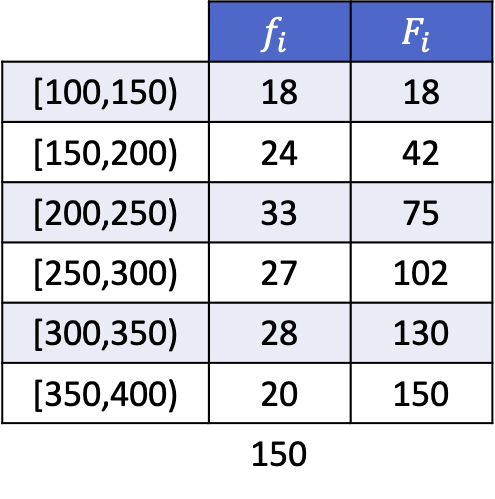
نظرًا لأنه تم تجميع البيانات، يجب علينا استخدام الطريقة التالية لحساب الشرائح الخمسية: حدد أولاً النطاق الذي تقع فيه الشريحة الخمسية، ثم ابحث عن القيمة الدقيقة للشريحة الخمسية.

وبالتالي، للعثور على الفترة التي يقع فيها الخُمس الأول، نستخدم الصيغة التالية:

سيكون الخُمس الأول في الفترة التي يكون تكرارها المطلق التراكمي أكبر مباشرة من 30.2، وهي في هذه الحالة الفترة [150,200) التي يكون ترددها المطلق التراكمي 42. وبمجرد أن نعرف الفاصل الزمني الخماسي، فإننا نطبق الصيغة الثانية من عملية تحديد قيمتها الدقيقة:

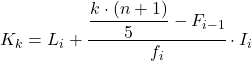
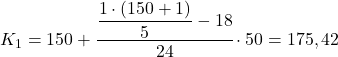
الآن نكرر نفس الإجراء للحصول على الخُمس الثاني، أولاً نحسب الفاصل الزمني الذي يقع فيه:

والتكرار المطلق التراكمي الذي يزيد مباشرة عن 60.4 هو 75، وبالتالي فإن النطاق الخمسي الثاني هو [200250). لذلك، نستبدل القيم المقابلة في الصيغة الثانية لحساب القيمة الخماسية الدقيقة:

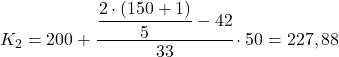
نقوم بنفس الإجراء مرة ثالثة للحصول على الخُمس 3. نحدد أولاً الفاصل الزمني الذي يقع فيه الخُمس:

يقع الخُمس في الفترة [250,300) لأن تكراره المطلق التراكمي (102) هو الذي يزيد مباشرة عن 90.6. وبالتالي فإن حساب القيمة الدقيقة للخُمس الثالث هو كما يلي:

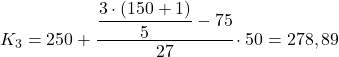
وأخيرًا، سنجد الخُمس الرابع. كما هو الحال دائمًا، نجد أولاً الفاصل الزمني:

الفاصل الزمني الذي يكون تكراره المطلق أكبر مباشرة من 120.8 هو [300.350)، وقيمته 130. وبالتالي فإن القيمة الدقيقة للشريحة الخمسية الرابعة ستكون: