الصيغ الإحصائية
ستجد هنا الصيغ الإحصائية الرئيسية. نتركك أيضًا مرتبطًا بمقالاتنا التي يمكنك من خلالها رؤية أمثلة لتطبيق كل صيغة إحصائية، بالإضافة إلى أنه يمكنك استخدام الآلة الحاسبة عبر الإنترنت حتى لا تضطر إلى إجراء الحسابات ومعرفة نتيجة الصيغة مباشرة.
صيغ القياسات الإحصائية للاتجاه المركزي
نصف
لحساب المتوسط، قم بجمع جميع القيم ثم قسمتها على إجمالي عدد البيانات. وبالتالي فإن صيغة المتوسط هي كما يلي:
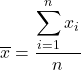
في الإحصاء، يُعرف المتوسط أيضًا بالمتوسط الحسابي أو المتوسط .
الوسيط
الوسيط هو القيمة الوسطى لجميع البيانات مرتبة من الأصغر إلى الأكبر. بمعنى آخر، يقوم الوسيط بتقسيم مجموعة البيانات المرتبة إلى جزأين متساويين.
يعتمد حساب الوسيط على ما إذا كان العدد الإجمالي للبيانات زوجيًا أم فرديًا:
- إذا كان العدد الإجمالي للبيانات فرديًا ، فسيكون الوسيط هو القيمة التي تقع في منتصف البيانات. وهذا يعني القيمة الموجودة في الموضع (n+1)/2 من البيانات المصنفة.
- إذا كان العدد الإجمالي لنقاط البيانات زوجيًا ، فسيكون الوسيط هو متوسط نقطتي البيانات الموجودتين في المركز. وهذا يعني المتوسط الحسابي للقيم الموجودة في الموضعين n/2 وn/2+1 من البيانات المطلوبة.
![]()
![]()
ذهب
![]()
هو إجمالي عدد البيانات في العينة ويشير الرمز Me إلى الوسيط.
موضة
في الإحصائيات، الوضع هو القيمة الموجودة في مجموعة البيانات التي لها أعلى تكرار مطلق، أي أن الوضع هو القيمة الأكثر تكرارًا في مجموعة البيانات.
لذلك، لا توجد صيغة محددة للوضع، ولكن لحساب وضع مجموعة البيانات الإحصائية، ما عليك سوى حساب عدد المرات التي يظهر فيها كل عنصر بيانات في العينة، وستكون البيانات الأكثر تكرارًا هي الوضع.
يمكن أيضًا القول أن الوضع هو الوضع الإحصائي أو القيمة المشروطة .
صيغ القياسات الإحصائية للتشتت
الانحراف المعياري
الانحراف المعياري، ويسمى أيضًا الانحراف المعياري، يساوي الجذر التربيعي لمجموع مربعات انحرافات سلسلة البيانات مقسومًا على إجمالي عدد الملاحظات.
وبالتالي فإن صيغة الانحراف المعياري هي:
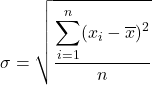
التباين
التباين يساوي مجموع مربعات البقايا على إجمالي عدد الملاحظات. وبالتالي فإن صيغة هذا المقياس الإحصائي هي كما يلي:

ذهب:
-

هو المتغير العشوائي الذي تريد حساب التباين له.
-

هي قيمة البيانات

.
-

هو العدد الإجمالي للملاحظات.
-

هو متوسط المتغير العشوائي

.
معامل الاختلاف
في الإحصاء، معامل التباين هو مقياس للتشتت يستخدم لتحديد تشتت مجموعة البيانات بالنسبة لمتوسطها. يتم حساب معامل التباين عن طريق قسمة الانحراف المعياري للبيانات على وسطها، ثم الضرب في 100 للتعبير عن القيمة كنسبة مئوية.
![]()
مرتب
النطاق الإحصائي هو مقياس للتشتت يشير إلى الفرق بين القيمة القصوى والحد الأدنى لقيمة البيانات في العينة. ولذلك، لحساب مدى السكان أو العينة الإحصائية، يجب طرح القيمة القصوى من القيمة الدنيا.
![]()
النطاق الربيعي
المدى الربيعي ، ويسمى أيضًا المدى الربيعي ، هو مقياس للتشتت الإحصائي الذي يشير إلى الفرق بين الربعين الثالث والأول.
لذلك، لحساب النطاق الربيعي لمجموعة بيانات إحصائية، يجب عليك أولاً العثور على الربعين الثالث والأول ثم طرحهما.
![]()
فرق متوسط
متوسط الانحراف ، ويسمى أيضًا متوسط الانحراف المطلق ، هو متوسط الانحرافات المطلقة. وبالتالي فإن متوسط الانحراف يساوي مجموع انحرافات كل عنصر بيانات عن الوسط الحسابي مقسومًا على إجمالي عدد عناصر البيانات.
![]()
صيغ لقياسات الموقف الإحصائي
الربعيات
في الإحصاء، الربعيات هي القيم الثلاث التي تقسم مجموعة من البيانات المرتبة إلى أربعة أجزاء متساوية. وبالتالي، تمثل الشرائح الربعية الأولى والثانية والثالثة على التوالي 25% و50% و75% من جميع البيانات الإحصائية.
يتم تمثيل الربيعيات بحرف كبير Q ومؤشر الربعي، وبالتالي فإن الربع الأول هو Q 1 ، والربيع الثاني هو Q 2 ، والربيع الثالث هو Q 3 .
الصيغة الربعية هي:
![]()
يرجى ملاحظة: هذه الصيغة تخبرنا بموضع الربيع، وليس قيمة الربع. سيكون الربع هو البيانات الموجودة في الموضع الذي حصلت عليه الصيغة.
ومع ذلك، في بعض الأحيان نتيجة هذه الصيغة تعطينا عددًا عشريًا. ولذلك يجب علينا التمييز بين حالتين اعتمادًا على ما إذا كانت النتيجة رقمًا عشريًا أم لا:
- إذا كانت نتيجة الصيغة رقمًا بدون جزء عشري ، فإن الربع هو البيانات الموجودة في الموضع الذي توفره الصيغة أعلاه.
- إذا كانت نتيجة الصيغة رقمًا بجزء عشري ، فسيتم حساب القيمة الربعية باستخدام الصيغة التالية:
![]()
حيث x i و x i+1 هما أرقام المواضع التي يقع بينها الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى، و d هو الجزء العشري من الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى.
أعشارية
في الإحصاء، العشريات هي القيم التسع التي تقسم مجموعة من البيانات المرتبة إلى عشرة أجزاء متساوية. بحيث يمثل العُشر الأول والثاني والثالث 10%، 20%، 30%،… من العينة أو السكان.
يتم تمثيل العشريات بالحرف الكبير D ومؤشر العشري، أي أن العشري الأول هو D 1 ، والعشيري الثاني هو D 2 ، والعشيري الثالث هو D 3 ، وما إلى ذلك.
الصيغة العشرية هي كما يلي:
![]()
يرجى ملاحظة: هذه الصيغة تخبرنا بموضع العلامة العشرية، وليس قيمة العلامة العشرية. سيكون العشري هو البيانات الموجودة في الموضع الذي حصلت عليه الصيغة.
لكن في بعض الأحيان نتيجة هذه الصيغة تعطينا رقما عشريا، لذلك يجب علينا التمييز بين حالتين اعتمادا على ما إذا كانت النتيجة رقما عشريا أم لا:
- إذا كانت نتيجة الصيغة رقمًا بدون جزء عشري ، فإن العلامة العشرية هي البيانات الموجودة في الموضع الذي توفره الصيغة أعلاه.
- إذا كانت نتيجة الصيغة رقمًا بجزء عشري ، فسيتم حساب القيمة العشرية باستخدام الصيغة التالية:
![]()
حيث x i و x i+1 هما أرقام المواضع التي يقع بينها الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى، و d هو الجزء العشري من الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى.
النسب المئوية
في الإحصاء، النسب المئوية هي القيم التي تقسم مجموعة من البيانات المرتبة إلى مائة جزء متساوي. لذا، تشير النسبة المئوية إلى القيمة التي تقل عنها نسبة مئوية من مجموعة البيانات.
يتم تمثيل النسب المئوية بالحرف الكبير P والمؤشر المئوي، أي أن المئين الأول هو P 1 ، والمئين الأربعين هو P 40 ، والمئين 79 هو P 79 ، وما إلى ذلك.
الصيغة المئوية هي:
![]()
يرجى ملاحظة: هذه الصيغة تخبرنا بموضع النسبة المئوية، وليس قيمتها. ستكون النسبة المئوية هي البيانات الموجودة في الموضع الذي حصلت عليه الصيغة.
لكن في بعض الأحيان نتيجة هذه الصيغة تعطينا رقما عشريا، لذلك يجب علينا التمييز بين حالتين اعتمادا على ما إذا كانت النتيجة رقما عشريا أم لا:
- إذا كانت نتيجة الصيغة عبارة عن رقم بدون جزء عشري ، فإن النسبة المئوية تتوافق مع البيانات الموجودة في الموضع الذي توفره الصيغة أعلاه.
- إذا كانت نتيجة الصيغة رقمًا بجزء عشري ، فسيتم حساب القيمة المئوية الدقيقة باستخدام الصيغة التالية:
![]()
حيث x i و x i+1 هما أرقام المواضع التي يقع بينها الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى، و d هو الجزء العشري من الرقم الذي تم الحصول عليه بواسطة الصيغة الأولى.
صيغ قياس الشكل الإحصائي
معامل عدم التماثل
معامل الانحراف، أو مؤشر الانحراف، هو معامل إحصائي يستخدم لتحديد انحراف التوزيع. لذلك، من خلال حساب معامل عدم التماثل، يمكنك معرفة نوع عدم التماثل في التوزيع دون الحاجة إلى عمل تمثيل بياني له.
صيغة معامل عدم التماثل هي كما يلي:
![]()
وبشكل مكافئ، يمكن استخدام أي من الصيغتين التاليتين لحساب معامل عدم تناسق فيشر:
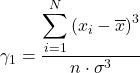
![]()
ذهب
![]()
هو التوقع الرياضي،
![]()
المتوسط الحسابي،
![]()
الانحراف المعياري و
![]()
العدد الإجمالي للبيانات.
معامل التفرطح
يشير التفرطح، الذي يُطلق عليه أيضًا الحدة، إلى مدى تركيز التوزيع حول متوسطه. وبعبارة أخرى، يشير التفرطح إلى ما إذا كان التوزيع حادًا أم مسطحًا. على وجه التحديد، كلما زاد التفرطح في التوزيع، كلما كان أكثر انحدارًا (أو أكثر حدة).
صيغة معامل التفرطح هي كما يلي:
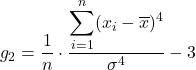
ذهب
![]()
هي القيمة المقابلة للملاحظة
![]()
,
![]()
المتوسط الحسابي،
![]()
الانحراف المعياري و
![]()
العدد الإجمالي للبيانات.
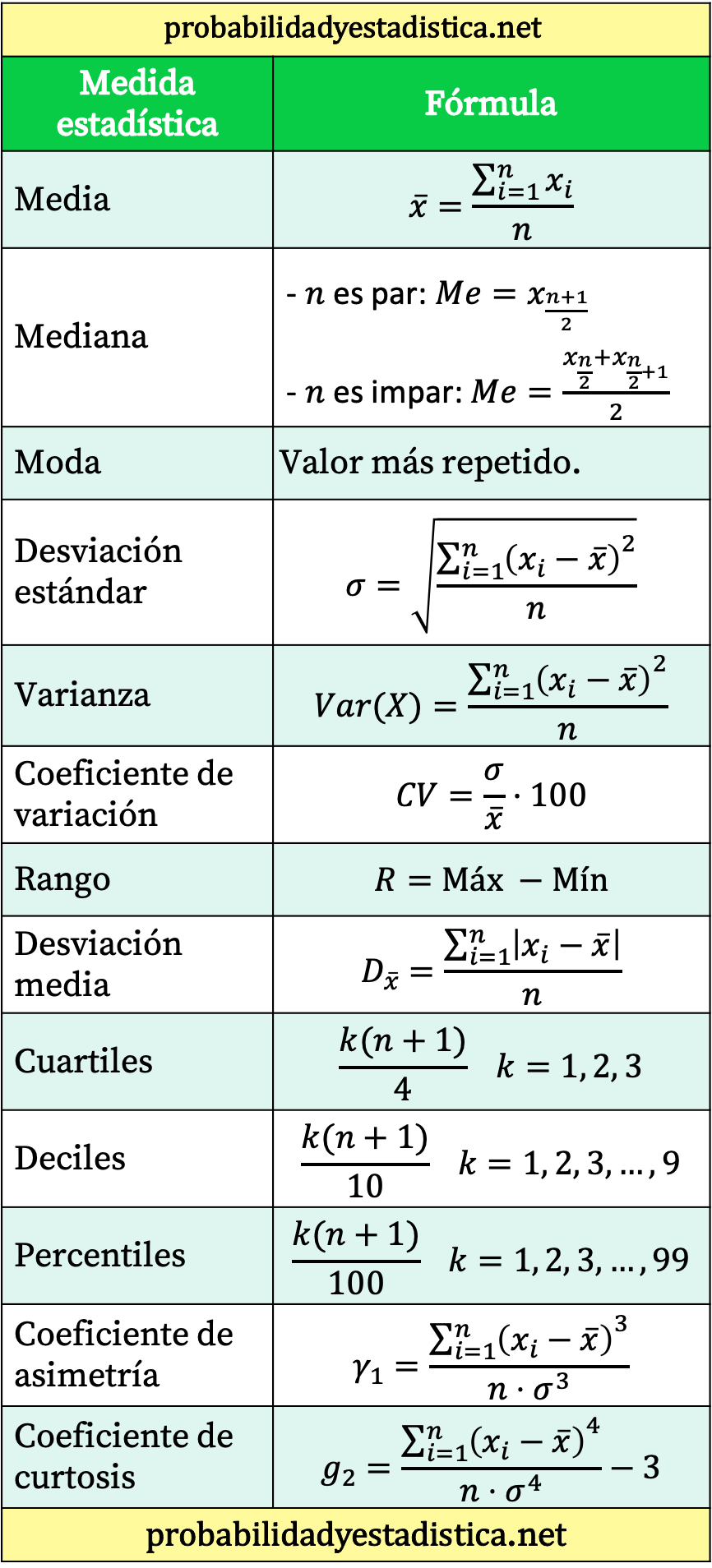
جدول ملخص لجميع الصيغ الإحصائية
وأخيرا، نترك لكم جدولا يلخص أهم المعادلات الإحصائية.