العمليات على المجموعات: الاتحاد والتقاطع والتكامل والفرق
المجموعة هي مجموعة من العناصر.
نقوم بتعيين مجموعة بحرف كبير ونحدد عناصر المجموعة باستخدام الأقواس المتعرجة. على سبيل المثال، لنفترض أن لدينا مجموعة تسمى “أ” تحتوي على العناصر 1، 2، 3. سنكتب ذلك على النحو التالي:
أ = {1، 2، 3}
يشرح هذا البرنامج التعليمي عمليات المجموعة الأكثر استخدامًا في الاحتمالات والإحصائيات.
اتحاد
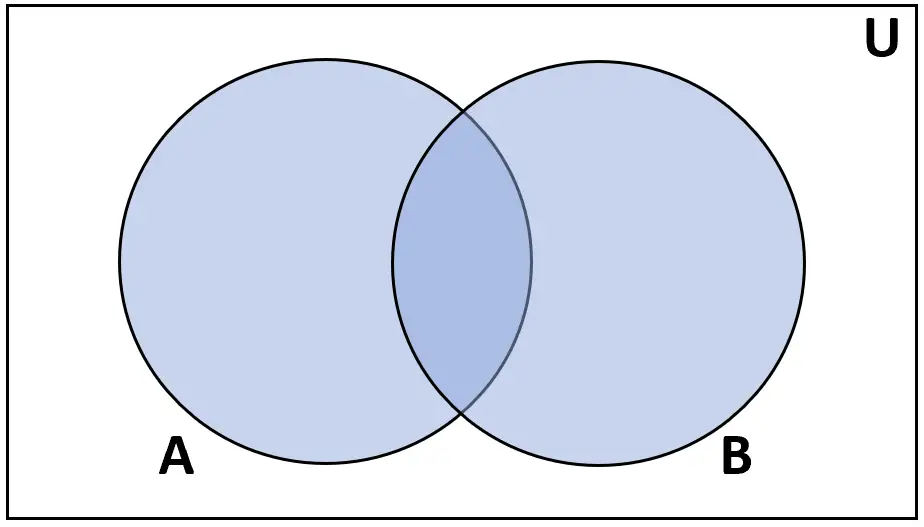
التعريف: اتحاد المجموعتين A وB هو مجموعة العناصر الموجودة إما في A أو في B.
التقييم: أ ∪ ب
أمثلة:
- {1، 2، 3} ∪ {4، 5، 6} = {1، 2، 3، 4، 5، 6}
- {1، 2} ∪ {1، 2} = {1، 2}
- {1، 2، 3} ∪ {3، 4} = {1، 2، 3، 4}
تداخل
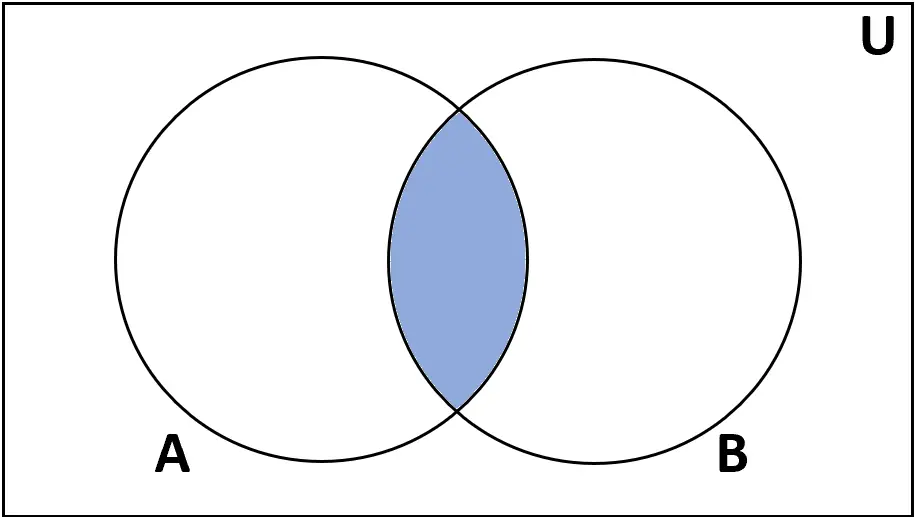
التعريف: تقاطع المجموعتين A وB هو مجموعة العناصر الموجودة في كل من A وB.
تدوين: أ ∩ ب
أمثلة:
- {1، 2، 3} ∩ {4، 5، 6} = {∅}
- {1، 2} ∩ {1، 2} = {1، 2}
- {1، 2، 3} ∩ {3، 4} = {3}
إطراء
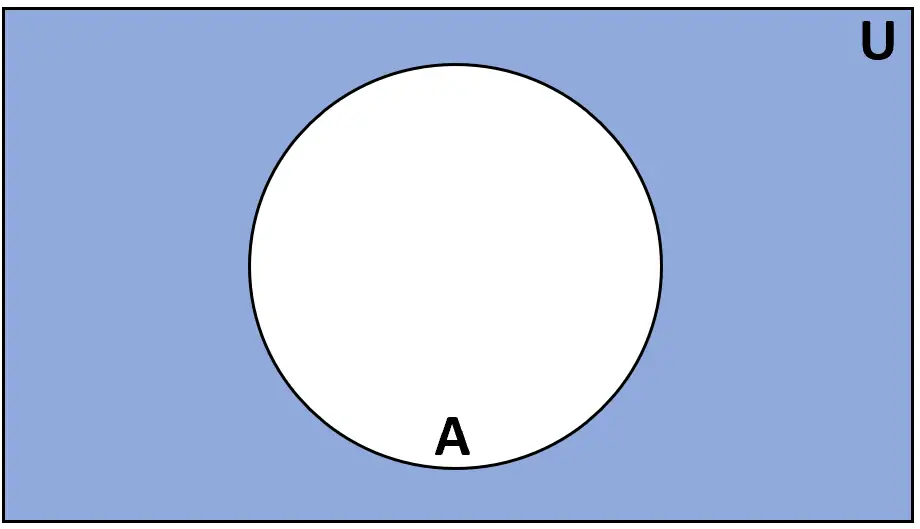
التعريف: مكملة المجموعة A هي مجموعة العناصر الموجودة في المجموعة العالمية U ولكنها ليست في A.
التقييم: A’ أو Ac
أمثلة:
- إذا كانت U = {1، 2، 3، 4، 5، 6} و A = {1، 2}، فإن A c = {3، 4، 5، 6}
- إذا كانت U = {1، 2، 3} و A = {1، 2}، فإن A c = {3}
اختلاف
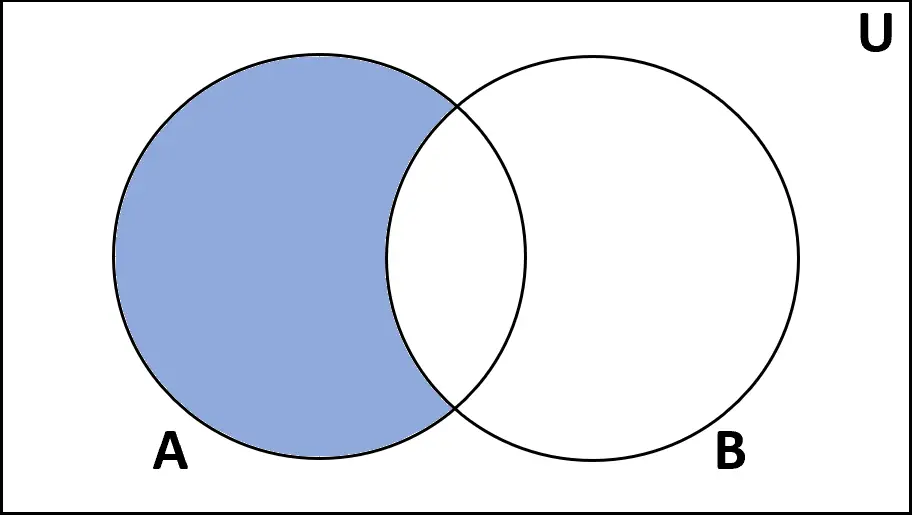
التعريف: الفرق بين المجموعتين A وB هو مجموعة العناصر الموجودة في A ولكن ليس في B.
التقييمات: أ – ب
أمثلة:
- {1، 2، 3} – {2، 3، 4} = {1}
- {1، 2} – {1، 2} = {∅}
- {1، 2، 3} – {4، 5} = {1، 2، 3}
اختلاف متماثل
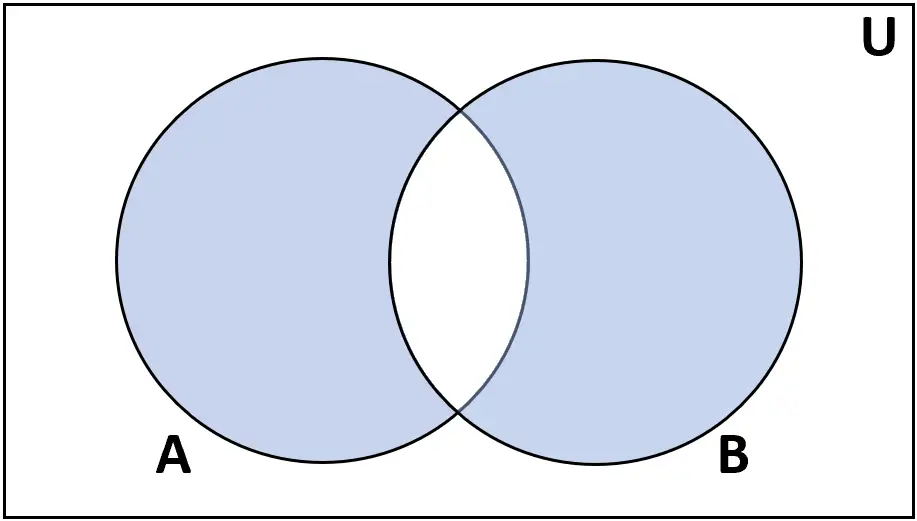
التعريف: الفرق المتماثل بين المجموعتين A وB هو مجموعة العناصر الموجودة في A أو B، ولكن ليس في كليهما.
التقييم: AΔB
أمثلة:
- {1، 2، 3} Δ {2، 3، 4} = {1، 4}
- {1, 2} Δ {1, 2} = {∅}
- {1، 2، 3} Δ {4، 5} = {1، 2، 3، 4، 5}
المنتج الديكارتي
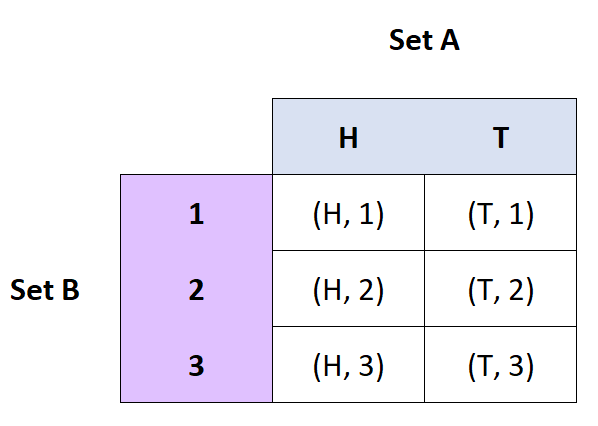
تعريف: المنتج الديكارتي للمجموعتين A وB هو مجموعة الأزواج المرتبة من A وB.
التقييم: أ × ب
أمثلة:
- إذا كان A = {H, T} وB = {1, 2, 3}، فإن A x B = {(H, 1)، (H، 2)، (H، 3)، (T، 1)، ( ت، ٢)، (ت، ٣)}
- إذا كان A = {T, H} وB = {1, 2, 3}، فإن A x B = {(T, 1)، (T، 2)، (T، 3)، (H، 1)، ( ح، 2)، (ح، 3)}