فهم فرضية العدم لنماذج anova

يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر.

يستخدم تحليل التباين الأحادي الفرضيات الصفرية والبديلة التالية:

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (جميع متوسطات المجموعة متساوية)
• _HA : يختلف متوسط مجموعة واحدة على الأقل   استراحة

لتحديد ما إذا كان ينبغي لنا رفض فرضية العدم أم لا، نحتاج إلى الرجوع إلى القيمة p في نتيجة جدول ANOVA.

إذا كانت القيمة p أقل من مستوى معين من الأهمية (على سبيل المثال 0.05)، فيمكننا رفض فرضية العدم ونستنتج أنه ليست كل وسائل المجموعة متساوية.

يتم استخدام ANOVA ثنائي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر تم تخصيصها لمتغيرين (تسمى أحيانًا “العوامل”).

يقوم ANOVA ثنائي الاتجاه باختبار ثلاث فرضيات صفرية في نفس الوقت:

• جميع متوسطات المجموعة متساوية عند كل مستوى من مستويات المتغير الأول
• جميع متوسطات المجموعة متساوية عند كل مستوى من مستويات المتغير الثاني
• لا يوجد أي تأثير للتفاعل بين المتغيرين

لتحديد ما إذا كان ينبغي علينا رفض كل فرضية صفرية أم لا، نحتاج إلى الرجوع إلى القيم الاحتمالية في نتيجة جدول ANOVA ثنائي الاتجاه.

توضح الأمثلة التالية كيفية تحديد ما إذا كان سيتم رفض الفرضية الصفرية في تحليل التباين أحادي الاتجاه وتحليل التباين ثنائي الاتجاه أم لا.

مثال 1: تحليل التباين أحادي الاتجاه

لنفترض أننا نريد أن نعرف ما إذا كانت ثلاثة برامج مختلفة للتحضير للاختبار تؤدي إلى متوسط درجات مختلفة في اختبار معين أم لا. ولاختبار ذلك، قمنا بتجنيد 30 طالبًا للمشاركة في إحدى الدراسات وتقسيمهم إلى ثلاث مجموعات.

يتم تعيين الطلاب في كل مجموعة عشوائيًا لاستخدام أحد برامج التحضير للاختبار الثلاثة للأسابيع الثلاثة التالية للتحضير للامتحان. وفي نهاية الأسابيع الثلاثة، يؤدي جميع الطلاب نفس الاختبار.

وفيما يلي نتائج الامتحانات لكل مجموعة:

عندما نقوم بإدخال هذه القيم في حاسبة ANOVA أحادية الاتجاه ، نحصل على جدول ANOVA التالي كمخرج:

لاحظ أن القيمة p هي 0.11385 .

في هذا المثال بالذات، سنستخدم الفرضيات الصفرية والبديلة التالية:

• H ₀ : μ ₁ = μ ₂ = μ ₃ (متوسط درجات الامتحان لكل مجموعة متساوي)
• _HA : يختلف متوسط مجموعة واحدة على الأقل   استراحة

وبما أن القيمة p لجدول ANOVA لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم.

وهذا يعني أنه ليس لدينا أدلة كافية لنقول بوجود فرق ذي دلالة إحصائية بين متوسط درجات الامتحانات للمجموعات الثلاث.

مثال 2: تحليل التباين ثنائي الاتجاه

لنفترض أن عالم النبات يريد معرفة ما إذا كان نمو النبات يتأثر بالتعرض لأشعة الشمس وتكرار الري.

تزرع 40 بذرة وتتركها تنمو لمدة شهرين في ظروف مختلفة من التعرض لأشعة الشمس وتكرار الري. وبعد شهرين، تسجل ارتفاع كل نبات. النتائج موضحة أدناه:

في الجدول أعلاه نرى أنه تم زراعة خمسة نباتات في كل مجموعة من الظروف.

على سبيل المثال، تمت زراعة خمسة نباتات بسقي يومي وبدون ضوء الشمس وكان ارتفاعها بعد شهرين 4.8 بوصة، 4.4 بوصة، 3.2 بوصة، 3.9 بوصة، 4.4 بوصة:

تقوم بإجراء ANOVA ثنائي الاتجاه في Excel وتحصل على النتيجة التالية:

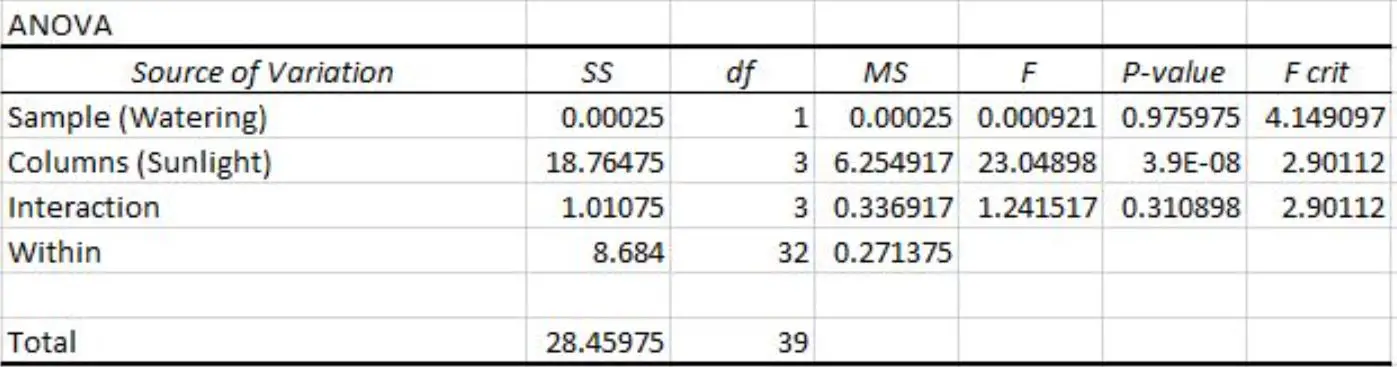
يمكننا أن نرى القيم p التالية في نتيجة جدول ANOVA ثنائي الاتجاه:

• القيمة p لتكرار الري هي 0.975975 . وهذا ليس ذو دلالة إحصائية عند مستوى دلالة 0.05.
• القيمة p للتعرض لأشعة الشمس هي 3.9E-8 (0.000000039) . وهذا ذو دلالة إحصائية عند مستوى دلالة 0.05.
• القيمة p للتفاعل بين تكرار الري والتعرض للشمس هي 0.310898 . وهذا ليس ذو دلالة إحصائية عند مستوى دلالة 0.05.

تشير هذه النتائج إلى أن التعرض لأشعة الشمس هو العامل الوحيد الذي له تأثير ذو دلالة إحصائية على ارتفاع النبات.

وبما أنه لا يوجد أي تأثير تفاعلي، فإن تأثير التعرض لأشعة الشمس يكون ثابتًا عند كل مستوى من مستويات تكرار الري.

ببساطة، ما إذا كان يتم ري النبات يوميًا أو أسبوعيًا ليس له أي تأثير على كيفية تأثير التعرض لأشعة الشمس على النبات.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول نماذج ANOVA:

كيفية تفسير قيمة F وقيمة P في ANOVA
كيفية حساب مجموع المربعات في تحليل التباين (ANOVA).
ماذا تعني قيمة F العالية في ANOVA؟