الافتراضات الثلاثة للتدابير المتكررة anova

يتم استخدام المقاييس المتكررة ANOVA لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات أو أكثر تظهر فيها نفس المواضيع في كل مجموعة أم لا.

ومع ذلك، قبل تنفيذ تدابير ANOVA المتكررة، يجب علينا التأكد من استيفاء الافتراضات التالية:

1. الاستقلال: يجب أن تكون كل ملاحظة مستقلة.

2. الحالة الطبيعية: يتم توزيع متغير الاستجابة بشكل طبيعي.

3. الكروية: يجب أن تكون تباينات الاختلافات بين جميع مجموعات المجموعات ذات الصلة متساوية.

إذا تم انتهاك واحد أو أكثر من هذه الافتراضات، فقد تكون نتائج التدابير المتكررة ANOVA غير موثوقة.

ونقدم في هذا المقال شرحًا لكل افتراض، وكيفية تحديد ما إذا كان الافتراض قد تحقق، وماذا تفعل إذا لم يتم تحقيقه.

الفرضية 1: الاستقلال

تفترض مقاييس ANOVA المتكررة أن كل ملاحظة في مجموعة البيانات الخاصة بك مستقلة عن جميع الملاحظات الأخرى.

كيفية تحديد ما إذا كان هذا الافتراض قد تم استيفاءه

إن أبسط طريقة للتحقق من هذا الافتراض هي التحقق من أن كل فرد في مجموعة البيانات تم أخذ عينات منه بشكل عشوائي من السكان باستخدام طريقة أخذ العينات العشوائية .

إذا تم استخدام طريقة أخذ العينات العشوائية، فيمكن افتراض أن كل ملاحظة مستقلة.

ماذا تفعل إذا لم يتم احترام هذا الافتراض

إذا لم يتم تحقيق هذا الافتراض، فهي مشكلة خطيرة لأن قيم كل فرد قد تكون مرتبطة ببعضها البعض بطريقة أو بأخرى.

غالبًا ما يكون العلاج الوحيد في هذا السيناريو هو تجنيد الأفراد لدراسة جديدة باستخدام طريقة أخذ العينات العشوائية.

الفرضية 2: الحياة الطبيعية

تفترض تدابير ANOVA المتكررة أن توزيع متغير الاستجابة يتم توزيعه بشكل طبيعي .

كيفية تحديد ما إذا كان هذا الافتراض قد تم استيفاءه

هناك طريقتان للتحقق من صحة هذه الفرضية:

1. قم بإنشاء رسم بياني أو مؤامرة QQ

يمكنك التحقق بصريًا مما إذا كان توزيع متغير الاستجابة يتم توزيعه بشكل طبيعي تقريبًا عن طريق إنشاء رسم بياني أو مخطط QQ.

إذا قمت بإنشاء رسم بياني ، فما عليك سوى التحقق من أن توزيع متغير الاستجابة يتبع شكل “الجرس” تقريبًا. إذا كان الأمر كذلك، يمكنك في كثير من الأحيان افتراض أن افتراض الحالة الطبيعية قد تم استيفاءه:

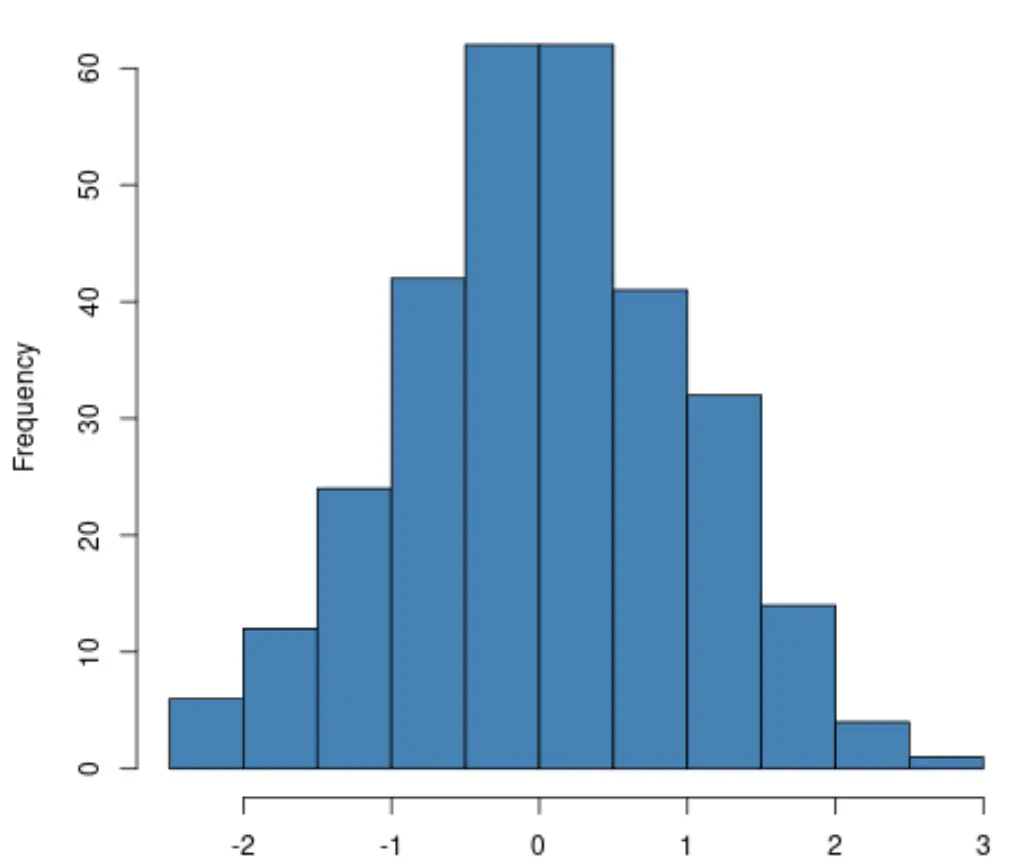
إذا كنت تقوم بإنشاء مخطط QQ ، فتحقق لمعرفة ما إذا كانت نقاط البيانات تقع على طول خط قطري مستقيم. إذا كان الأمر كذلك، فيمكنك عمومًا افتراض استيفاء افتراض الحالة الطبيعية:

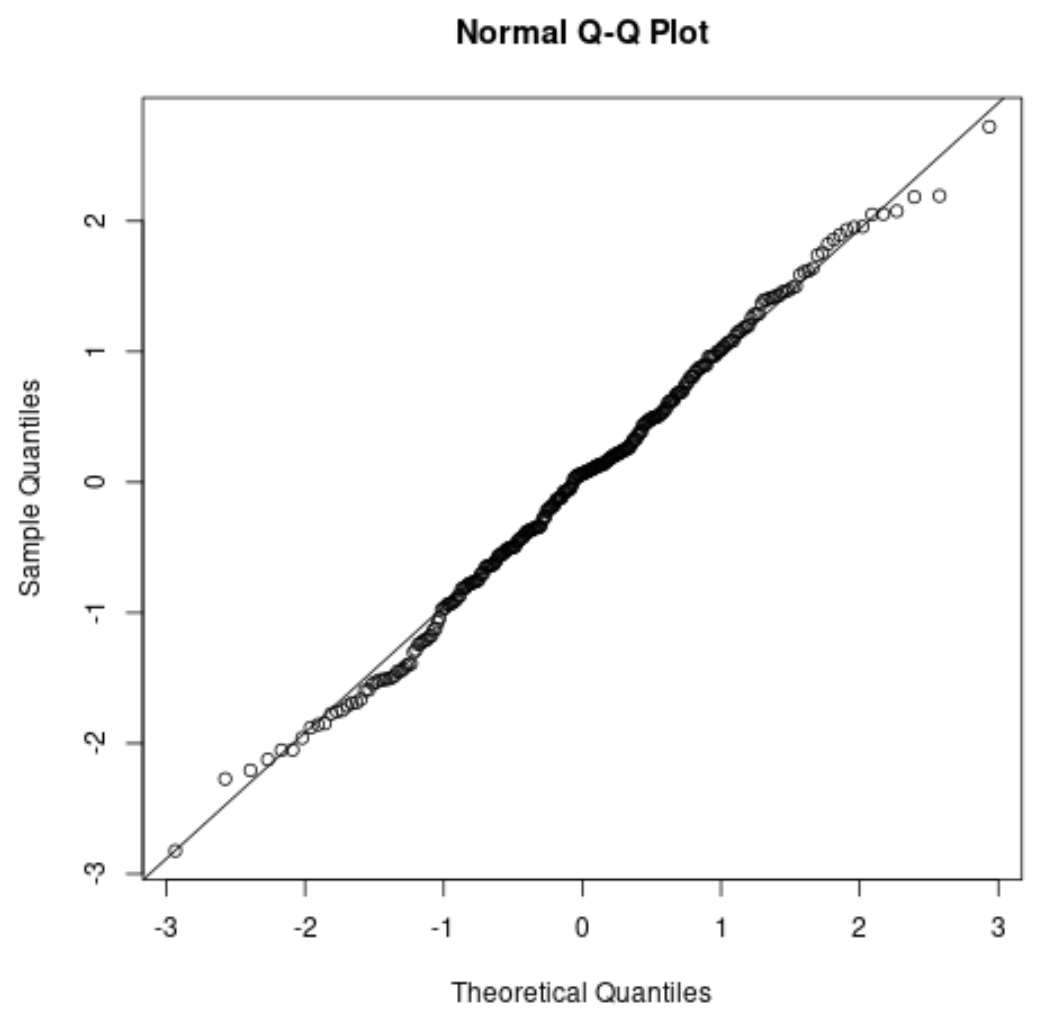
ذات صلة: كيفية استخدام مؤامرات QQ للتحقق من الحالة الطبيعية

2. إجراء اختبار إحصائي رسمي

يمكنك أيضًا إجراء اختبار شابيرو ويلك للتحقق من الحالة الطبيعية. إذا كانت القيمة p للاختبار أقل من 0.05، فهذا يشير إلى أن البيانات لا يتم توزيعها بشكل طبيعي.

ومع ذلك، يجب أن تدرك أنه عند العمل مع عينات كبيرة جدًا، فإن الاختبارات الإحصائية مثل اختبار شابيرو-ويلك ستخبرك دائمًا تقريبًا أن بياناتك ليست طبيعية.

لهذا السبب، غالبًا ما يكون من الأفضل فحص بياناتك بصريًا باستخدام الرسوم البيانية مثل الرسوم البيانية ومخططات QQ. بمجرد النظر إلى الرسوم البيانية، يمكنك الحصول على فكرة جيدة عما إذا كانت البيانات يتم توزيعها بشكل طبيعي أم لا.

ماذا تفعل إذا لم يتم احترام هذا الافتراض

بشكل عام، تعتبر التدابير المتكررة ANOVA قوية جدًا ضد انتهاكات افتراض الحالة الطبيعية طالما أن أحجام العينات كبيرة بما يكفي.

إذا تم انتهاك افتراض الحالة الطبيعية بشكل خطير، فلديك خياران:

1. قم بتحويل قيم الاستجابة لبياناتك بحيث يتم توزيع التوزيعات بشكل طبيعي أكثر.

2. إجراء اختبار غير معلمي مكافئ مثل اختبار فريدمان الذي لا يتطلب افتراض الحالة الطبيعية.

الافتراض 3: الكروية

تفترض المقاييس المتكررة أنوفا كروية – أي أن تباينات الاختلافات بين جميع مجموعات المجموعات ذات الصلة يجب أن تكون متساوية.

إذا لم يتم استيفاء هذا الافتراض، تصبح نسبة F متضخمة وتصبح نتائج القياسات المتكررة ANOVA غير موثوقة.

كيفية تحديد ما إذا كان هذا الافتراض قد تم استيفاءه

ولاختبار ما إذا كان هذا الافتراض قد تحقق أم لا، يمكننا إجراء اختبار موكلي للكروية.

يستخدم هذا الاختبار الفرضية الصفرية والبديلة التالية:

• ح ₀ : تباينات الفروق متساوية
• ح _أ : تباينات الفروق غير متساوية

إذا كانت القيمة p للاختبار أقل من مستوى معين من الأهمية (على سبيل المثال α = 0.05)، فإننا نرفض فرضية العدم ونستنتج أن تباينات الاختلافات ليست متساوية.

بخلاف ذلك، إذا كانت القيمة p لا تقل عن مستوى معين من الأهمية (على سبيل المثال α = 0.05)، فإننا نفشل في رفض فرضية العدم ونستنتج أن افتراض الكروية قد تم استيفائه.

اعتمادًا على البرنامج الإحصائي الذي تستخدمه، ستبدو نتائج هذا الاختبار كما يلي:

وبما أن القيمة p لا تقل عن 0.05، فسوف نفشل في رفض فرضية العدم ونستنتج أن افتراض الكروية قد تم استيفاءه في هذا المثال بالذات.

ماذا تفعل إذا لم يتم احترام هذا الافتراض

إذا رفضنا الفرضية الصفرية لاختبار Mauchly للكروية، فإننا نطبق عمومًا تصحيحًا على درجات الحرية المستخدمة لحساب قيمة F في جدول ANOVA للقياسات المتكررة.

هناك ثلاثة إصلاحات يمكننا تطبيقها:

• هيونه-فيلدت (الأقل تحفظًا)
• سيري-جيسر
• الحد الأدنى (الأكثر تحفظًا)

يميل كل من هذه التصحيحات إلى زيادة القيم p في جدول إخراج ANOVA للتدابير المتكررة لمراعاة حقيقة انتهاك افتراض الكروية.

يمكننا بعد ذلك استخدام هذه القيم p لتحديد ما إذا كان ينبغي لنا رفض الفرضية الصفرية للتدابير المتكررة ANOVA أم لا.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول التدابير المتكررة ANOVA:

مقدمة للتدابير المتكررة ANOVA
التدابير المتكررة حاسبة ANOVA
كيفية الإبلاغ عن نتائج التدابير المتكررة ANOVA
ANOVA في اتجاه واحد والتدابير المتكررة ANOVA: الفرق