ما هي المتغيرات العشوائية؟

المتغير العشوائي ، الذي يُشار إليه عمومًا بـ X، هو متغير تكون قيمه المحتملة هي نتائج عملية عشوائية.

هناك نوعان من المتغيرات العشوائية: منفصلة ومستمرة .

المتغيرات العشوائية المنفصلة

المتغير العشوائي المنفصل هو الذي لا يمكنه إلا أن يأخذ عددًا معدودًا من القيم المميزة مثل 0، 1، 2، 3، 4، 5…100، 1 مليون، إلخ. فيما يلي بعض الأمثلة على المتغيرات العشوائية المنفصلة:

• عدد المرات التي تهبط فيها العملة المعدنية بعد رميها 20 مرة.
• عدد المرات التي وصل فيها حجر النرد إلى الرقم 4 بعد رميه 100 مرة.
• عدد عناصر واجهة المستخدم المعيبة في صندوق مكون من 50 عنصر واجهة مستخدم.

يخبرنا التوزيع الاحتمالي للمتغير العشوائي المنفصل باحتمال أن يأخذ المتغير العشوائي قيمًا معينة.

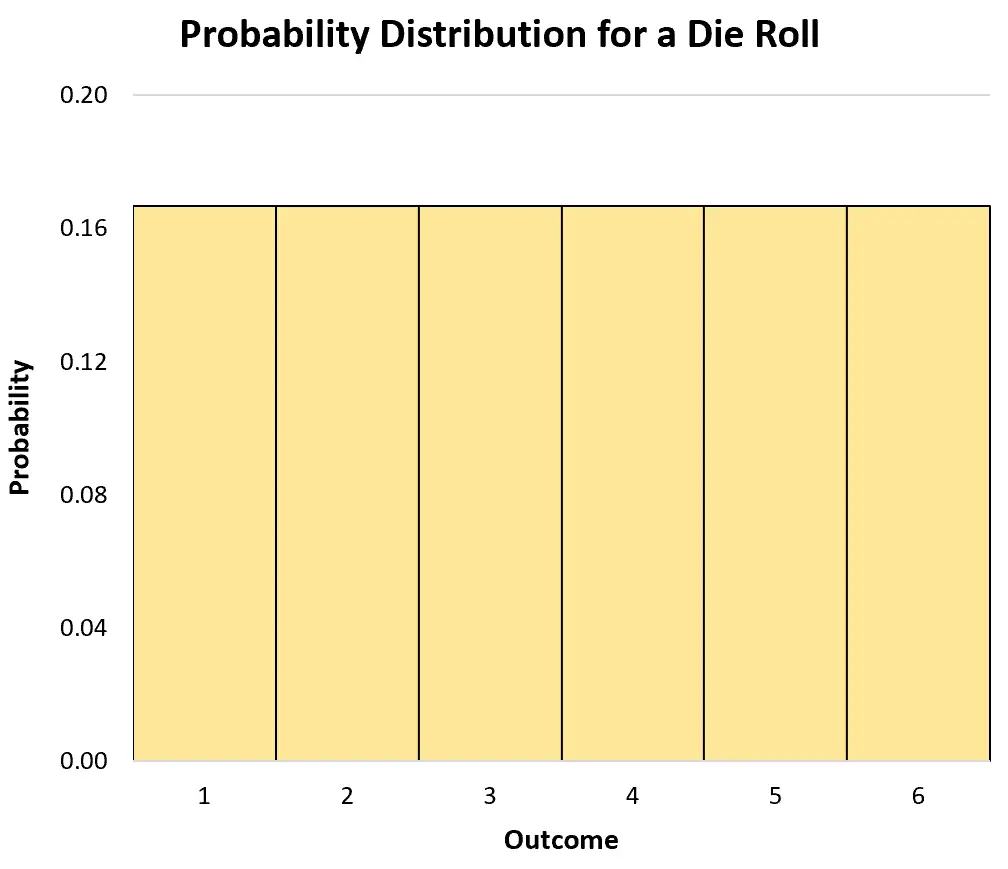
على سبيل المثال، لنفترض أننا ألقينا حجر نرد عادل مرة واحدة. إذا جعلنا X تشير إلى احتمال سقوط حجر النرد على رقم معين، فيمكن كتابة التوزيع الاحتمالي على النحو التالي:

• ف(س = 1): 1/6
• ف(س = 2): 1/6
• ف(س = 3): 1/6
• ف(س = 4): 1/6
• ف(س = 5): 1/6
• ف(س = 6): 1/6

ملحوظة:

لكي يكون التوزيع الاحتمالي صحيحا، يجب أن يستوفي المعيارين التاليين:

1. يجب أن يكون احتمال كل نتيجة بين 0 و 1.

2. مجموع كل الاحتمالات يجب أن يصل إلى 1.

لاحظ أن التوزيع الاحتمالي للفة القالب يلبي كلا المعيارين التاليين:

1. احتمال كل نتيجة يتراوح بين 0 و 1.

2. مجموع كل الاحتمالات يصل إلى 1.

يمكننا استخدام الرسم البياني لتصور التوزيع الاحتمالي:

يخبرنا التوزيع الاحتمالي التراكمي لمتغير عشوائي منفصل باحتمال أن يأخذ المتغير قيمة تساوي أو تقل عن قيمة معينة.

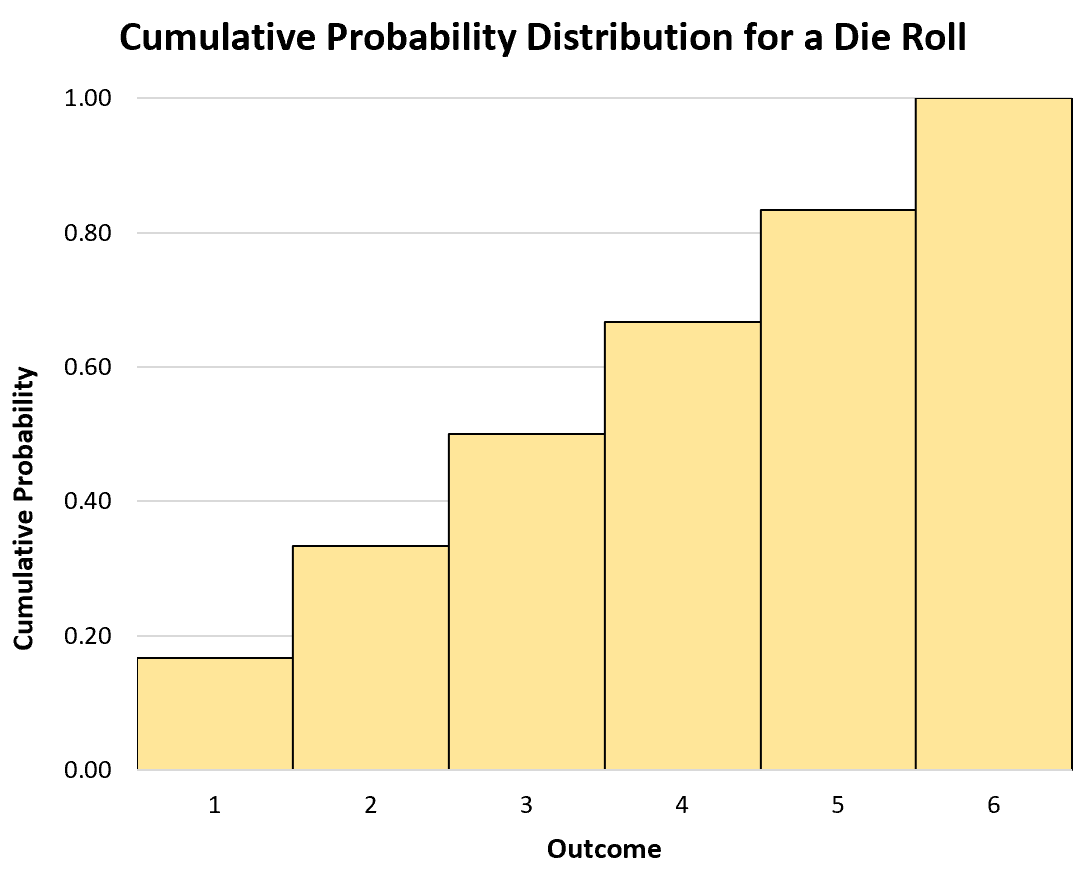
على سبيل المثال، قد يبدو التوزيع الاحتمالي التراكمي لرمية القالب كما يلي:

• ف (X ≥1): 1/6
• ف (X ≥2): 2/6
• ف (X ≥3): 3/6
• ف (X ≥4): 4/6
• ف (X ≥5): 5/6
• ف (X ≥6): 6/6

إن فرصة سقوط القالب على رقم واحد أو أقل هي ببساطة 1/6، لأنه لا يمكن أن يستقر على رقم أقل من واحد.

احتمال هبوطها على اثنين أو أقل هو P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6.

وبالمثل، فإن احتمال هبوطه على ثلاثة أو أقل هو P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6 و قريباً.

يمكننا أيضًا استخدام الرسم البياني لتصور التوزيع الاحتمالي التراكمي:

المتغيرات العشوائية المستمرة

المتغير العشوائي المستمر هو متغير يمكن أن يأخذ عددًا لا نهائيًا من القيم الممكنة. فيما يلي بعض الأمثلة على المتغيرات العشوائية المستمرة:

• وزن الحيوان
• ارتفاع الشخص
• الوقت اللازم لتشغيل الماراثون

على سبيل المثال، يمكن أن يكون ارتفاع الشخص 60.2 بوصة، 65.2344 بوصة، 70.431222 بوصة، وما إلى ذلك. هناك عدد لا حصر له من القيم الممكنة للحجم.

قاعدة عامة:

إذا كان بإمكانك حساب عدد النتائج، فأنت تعمل مع متغير عشوائي منفصل – على سبيل المثال، حساب عدد المرات التي تظهر فيها العملة المعدنية.

ولكن إذا كان بإمكانك قياس النتيجة، فأنت تعمل مع متغير عشوائي مستمر – على سبيل المثال قياس الطول والوزن والوقت وما إلى ذلك.

يخبرنا التوزيع الاحتمالي لمتغير عشوائي مستمر باحتمال أن يأخذ المتغير العشوائي قيمًا معينة.

ومع ذلك، على عكس التوزيع الاحتمالي للمتغيرات العشوائية المنفصلة، لا يمكن استخدام التوزيع الاحتمالي للمتغير العشوائي المستمر إلا لإخبارنا باحتمال أن يأخذ المتغير نطاقًا من القيم.

على سبيل المثال، لنفترض أننا نريد معرفة احتمال أن يكون وزن قطعة همبرغر من مطعم معين ربع رطل (0.25 رطل). وبما أن الوزن متغير مستمر، فإنه يمكن أن يأخذ عددا لا حصر له من القيم.

على سبيل المثال، قد يزن همبرغر معين في الواقع 0.250001 رطل، أو 0.24 رطل، أو 0.2488 رطل. احتمال أن يزن همبرغر معين 0.25 رطل بالضبط هو صفر.

لذلك يمكننا فقط استخدام التوزيع الاحتمالي لإخبارنا باحتمال أن يكون وزن الهامبرغر أقل من 0.25 رطل، أو أكثر من 0.25 رطل، أو بين نطاق معين (على سبيل المثال، بين 0.23 رطل و0.27 رطل).

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول المتغيرات العشوائية:

ما هي المتغيرات العشوائية iid؟
10 أمثلة للمتغيرات العشوائية في الحياة الحقيقية