كيفية تفسير المؤامرات التشخيصية في r

تُستخدم نماذج الانحدار الخطي لوصف العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة.

ومع ذلك، بمجرد تركيب نموذج الانحدار، فمن الجيد أيضًا إنتاج مخططات تشخيصية لتحليل بقايا النموذج والتأكد من أن النموذج الخطي مناسب للاستخدام مع البيانات المحددة التي نعمل معها.

يشرح هذا البرنامج التعليمي كيفية إنشاء وتفسير المخططات التشخيصية لنموذج انحدار معين في R.

مثال: إنشاء وتفسير المخططات التشخيصية في R

لنفترض أننا نلائم نموذج الانحدار الخطي البسيط باستخدام “ساعات الدراسة” للتنبؤ “بدرجة الامتحان” للطلاب في فصل معين:

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

يمكننا استخدام الأمر plot() لإنتاج أربع مخططات تشخيصية لنموذج الانحدار هذا:

 #produce diagnostic plots for regression model
plot(model)

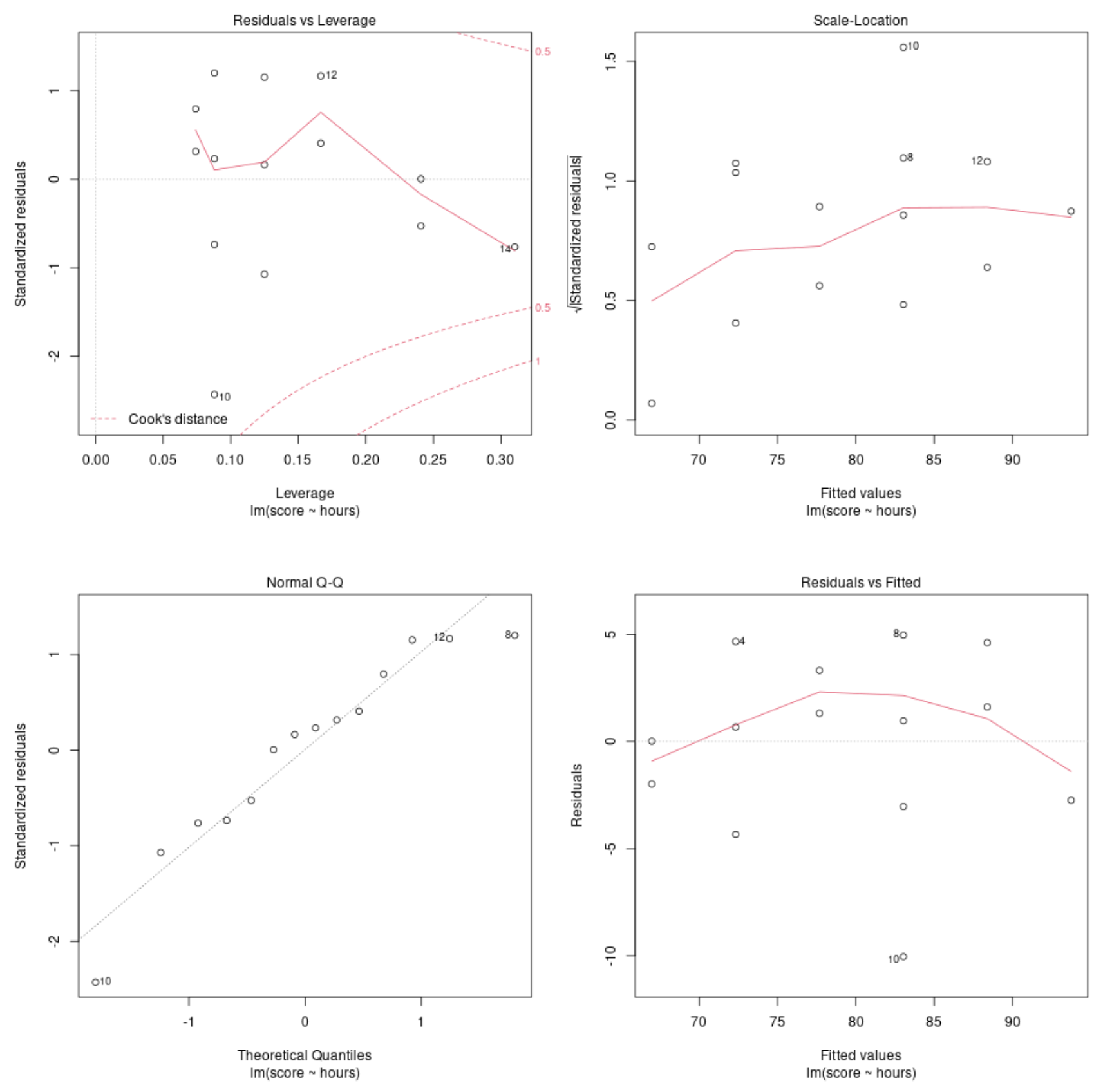
المخطط التشخيصي رقم 1: البقايا مقابل. الرسم البياني للرافعة المالية

يستخدم هذا الرسم البياني لتحديد الملاحظات المؤثرة. إذا كانت أي نقطة على هذا الرسم البياني تقع خارج مسافة كوك (الخطوط المنقطة)، فهذه ملاحظة مؤثرة.

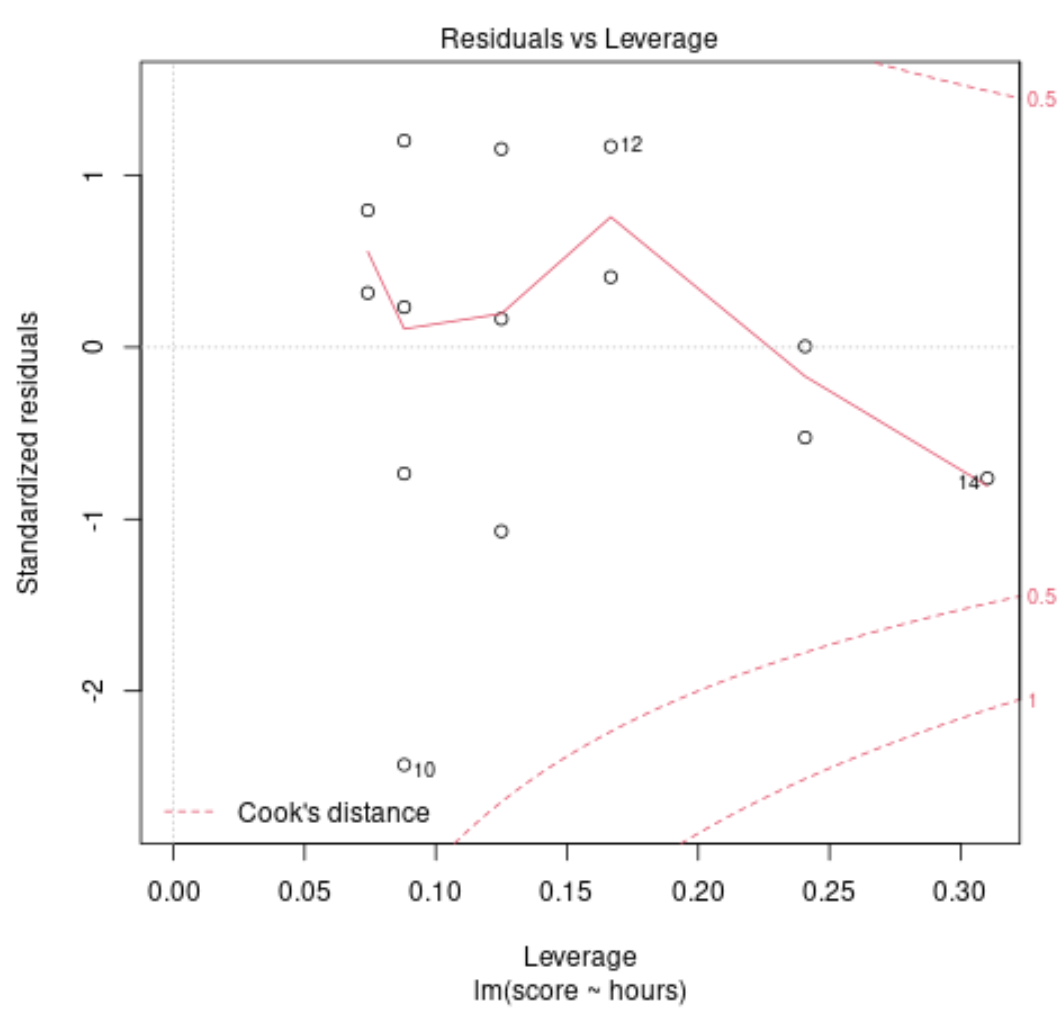
في مثالنا، يمكننا أن نرى أن الملاحظة رقم 10 هي الأقرب إلى حد مسافة كوك، ولكنها لا تقع خارج الخط المنقط. وهذا يعني أنه لا توجد نقاط مؤثرة بشكل مفرط في مجموعة البيانات لدينا.

المؤامرة التشخيصية رقم 2: مؤامرة النطاق والموقع

يستخدم هذا الرسم البياني للتحقق من افتراض مساواة التباين (وتسمى أيضًا “التجانس”) بين بقايا نموذج الانحدار الخاص بنا. إذا كان الخط الأحمر أفقيًا تقريبًا على المخطط، فمن المحتمل أن يتم تحقيق افتراض التباين المتساوي.

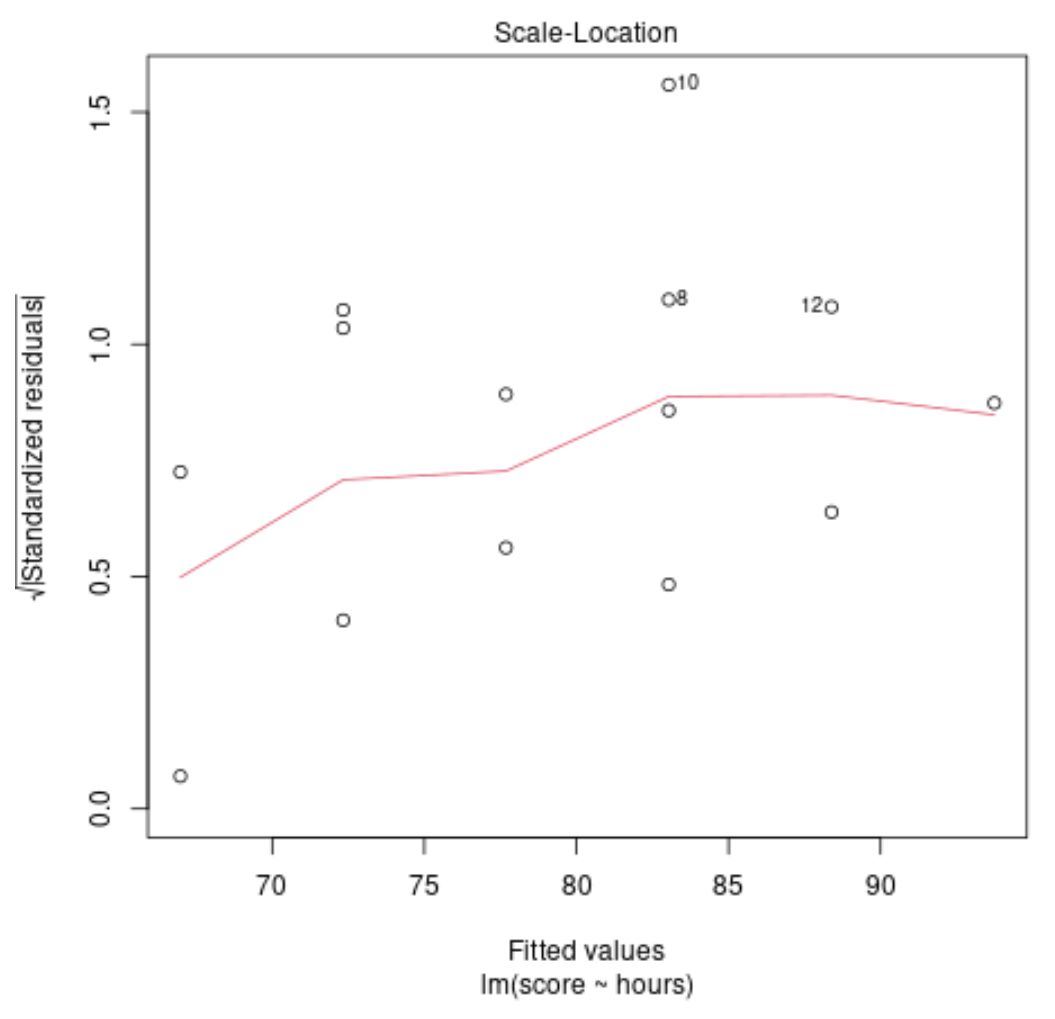
في مثالنا، يمكننا أن نرى أن الخط الأحمر ليس أفقيًا تمامًا على قطعة الأرض، لكنه لا ينحرف بشدة عند أي نقطة. ربما نذكر أن افتراض التباين المتساوي لم يتم انتهاكه في هذه الحالة.

ذات صلة: فهم التغايرية في تحليل الانحدار

التتبع التشخيصي رقم 3: تتبع QQ العادي

يتم استخدام هذه المؤامرة لتحديد ما إذا كانت البقايا من نموذج الانحدار يتم توزيعها بشكل طبيعي. إذا كانت النقاط على هذا الرسم البياني تقع تقريبًا على طول خط قطري مستقيم، فيمكننا أن نفترض أن البقايا موزعة بشكل طبيعي.

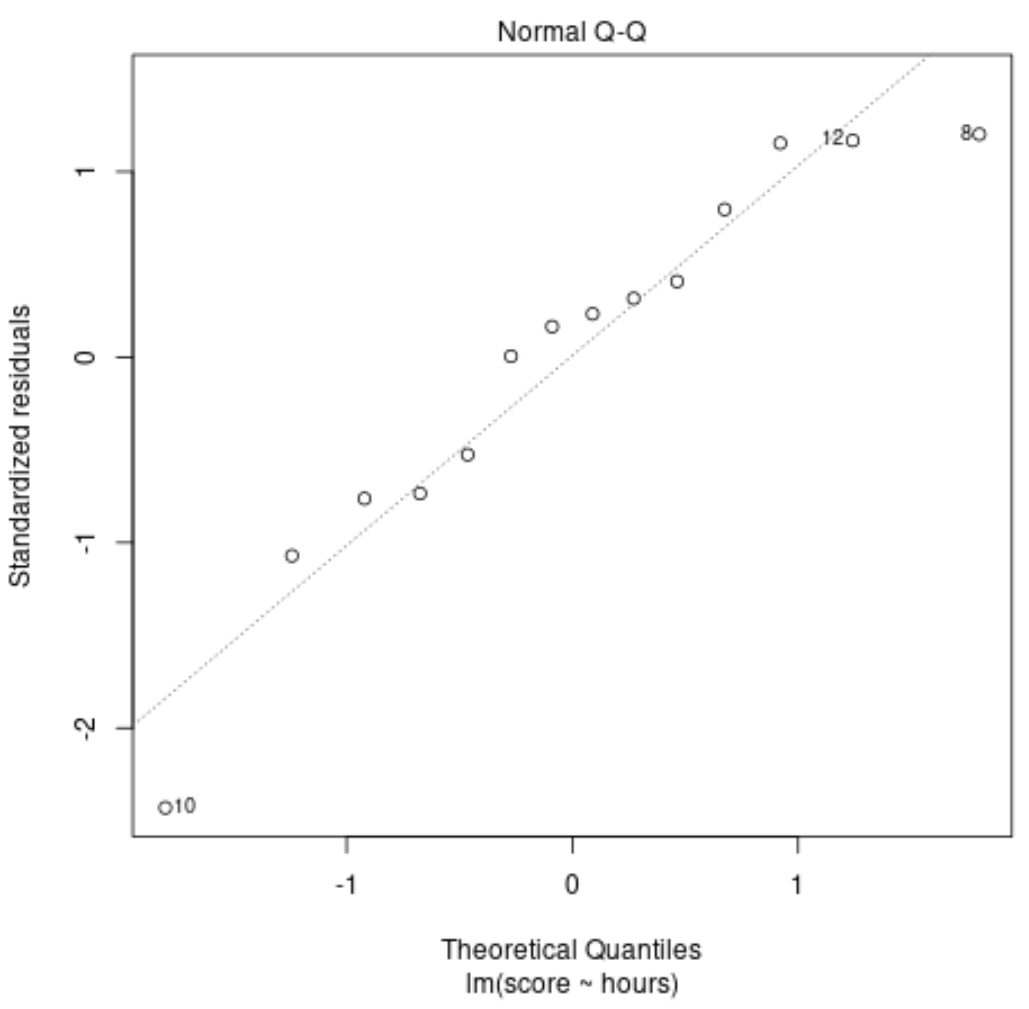
في مثالنا، يمكننا أن نرى أن النقاط تقع تقريبًا على طول الخط المستقيم القطري. الملاحظتان رقم 10 ورقم 8 تنحرفان قليلاً عن الخط الموجود في النهايتين، ولكن ليس بما يكفي للإعلان عن عدم توزيع البقايا بشكل طبيعي.

المؤامرة التشخيصية رقم 4: المخلفات مقابل المخلفات مؤامرة المعدلة

يتم استخدام هذه المؤامرة لتحديد ما إذا كانت البقايا تظهر أنماطًا غير خطية. إذا كان الخط الأحمر في وسط المخطط أفقيًا تقريبًا، فيمكننا أن نفترض أن البقايا تتبع نمطًا خطيًا.

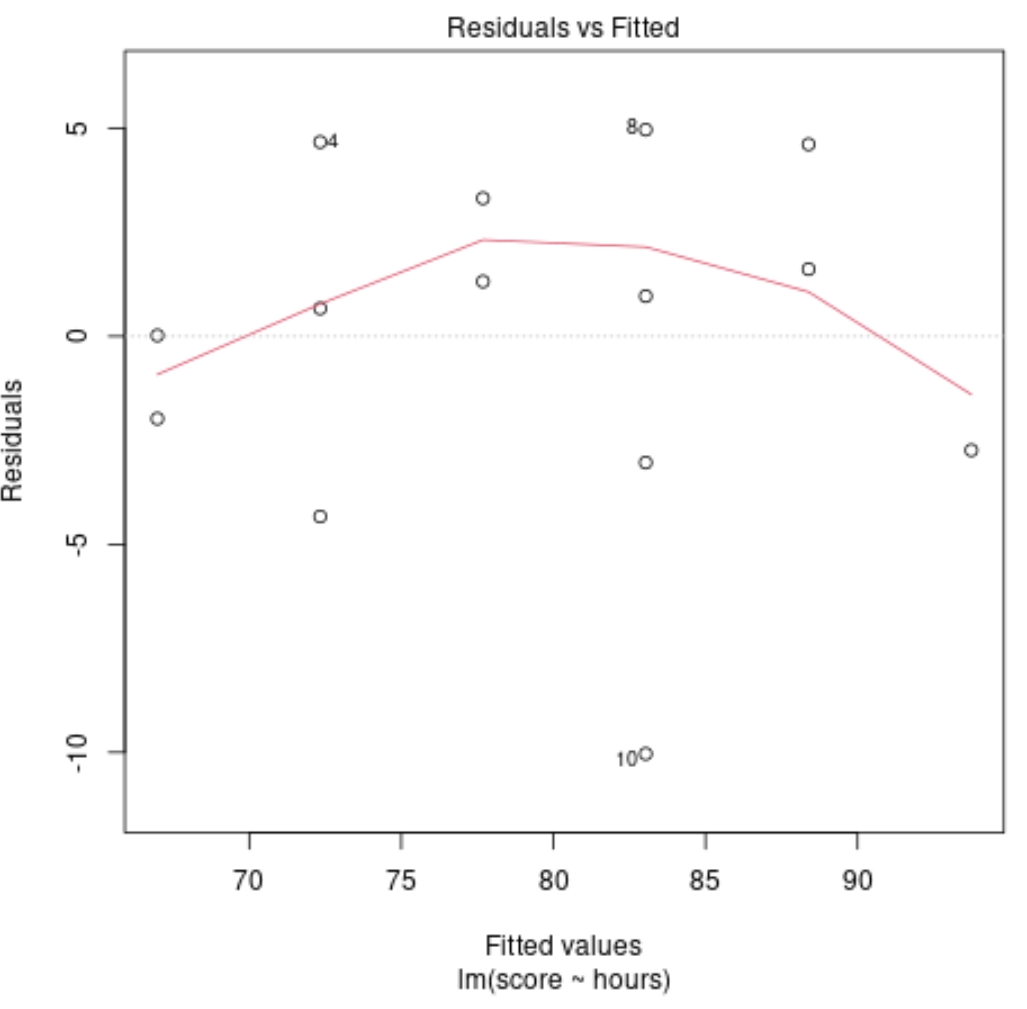
في مثالنا، يمكننا أن نرى أن الخط الأحمر ينحرف عن الخط الأفقي المثالي ولكن ليس بشكل كبير. من المحتمل أن نشير إلى أن البقايا تتبع نمطًا خطيًا تقريبًا وأن نموذج الانحدار الخطي مناسب لمجموعة البيانات هذه.

مصادر إضافية

الافتراضات الأربعة للانحدار الخطي
ما هي البقايا في الإحصاء؟
كيفية إنشاء قطعة أرض متبقية في R
كيفية تفسير مقياس ومؤامرة الموقع