المربعات السفلية
تشرح هذه المقالة ما هي المربعات الصغرى في الإحصائيات، وما هي طريقة المربعات الصغرى، وكيف يتم ملاءمة نموذج الانحدار بمعيار المربعات الصغرى.
ما هي طريقة المربعات الصغرى؟
طريقة المربعات الصغرى هي طريقة إحصائية تستخدم لتحديد معادلة الانحدار. بمعنى آخر، تعد طريقة المربعات الصغرى معيارًا يستخدم في نموذج الانحدار لتقليل الخطأ الذي يتم الحصول عليه عند حساب معادلة الانحدار.
وبشكل ملموس، تتكون طريقة المربعات الصغرى من تقليل مجموع مربعات البقايا، أو بمعنى آخر، تعتمد على تقليل مجموع مربعات الفروق بين القيم التي تنبأ بها نموذج الانحدار والقيم المرصودة . . أدناه سنرى بالتفصيل كيف يتم ملاءمة نموذج الانحدار بمعيار المربعات الصغرى.
الميزة الرئيسية لطريقة المربعات الصغرى هي تقليل المسافات الأطول بين القيم المرصودة ووظيفة الانحدار. على عكس معايير الانحدار الأخرى، تعتبر طريقة المربعات الصغرى أن تقليل المخلفات الكبيرة أكثر أهمية من المخلفات الصغيرة، نظرًا لأن مربع العدد الكبير أكبر بكثير من مربع الرقم الصغير. رقم.
خطأ في التقدير
لفهم مفهوم المربعات الصغرى بشكل كامل، يجب علينا أولاً أن نكون واضحين بشأن ماهية القيم المتبقية في نموذج الانحدار. لذلك سنرى أدناه ما هو خطأ التقدير وكيفية حسابه.
في الإحصائيات، خطأ التقدير ، والذي يسمى أيضًا المتبقي ، هو الفرق بين القيمة الحقيقية والقيمة التي يوفرها نموذج الانحدار. وبالتالي يتم حساب المتبقي الإحصائي على النحو التالي:
![]()
ذهب:
-

هو ما تبقى من البيانات ط.
-

هي القيمة الحقيقية للبيانات أنا.
-

هي القيمة التي يوفرها نموذج الانحدار للبيانات i.
وبالتالي، كلما زاد حجم الجزء المتبقي من قطعة من البيانات، كلما كان تكييف نموذج الانحدار مع هذه القطعة من البيانات أكثر سوءًا. وبالتالي، كلما كان المبلغ المتبقي أصغر، قلت المسافة بين قيمته الفعلية وقيمته المتوقعة.
وبالمثل، إذا كان الجزء المتبقي من جزء من البيانات موجبًا، فهذا يعني أن نموذج الانحدار يتنبأ بقيمة أقل من القيمة الحقيقية. أما إذا كانت القيمة المتبقية سالبة، فهذا يعني أن القيمة المتوقعة أكبر من القيمة الفعلية.
تقليل مربعات الخطأ
الآن بعد أن عرفنا ما هو المتبقي في الإحصائيات، سيكون من الأسهل فهم كيفية تقليل مربعات الخطأ إلى الحد الأدنى.
مربع الخطأ هو مربع المتبقي، لذا فإن مربع الخطأ يساوي الفرق بين القيمة الحقيقية والقيمة التي يوفرها نموذج الانحدار مرفوعة للأس اثنين.
![]()
ذهب:
-
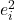
هو مربع ما تبقى من البيانات ط.
-

هي القيمة الحقيقية للبيانات أنا.
-

هي القيمة التي يوفرها نموذج الانحدار للبيانات i.
وبالتالي، فإن طريقة المربعات الصغرى تتكون من إنشاء نموذج انحدار عن طريق تقليل مجموع مربعات الأخطاء . لذلك يعتمد معيار المربعات الصغرى على تصغير التعبير التالي:
![Rendered by QuickLaTeX.com \begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0a82d4d723b77093b4d584609f372cd7_l3.png)
ولهذا السبب يُسمى معيار المربعات الصغرى أيضًا بمعيار المربعات الصغرى.
كما ترون في الصيغة السابقة، فإن معيار المربعات الصغرى يعطي أهمية أكبر لتقليل المخلفات الكبيرة من المخلفات الصغيرة. على سبيل المثال، إذا كان أحد العناصر المتبقية هو 3 والباقي الآخر هو 5، فإن مربعيهما هما 9 و25 على التوالي، وبالتالي فإن معيار المربعات الصغرى سيعطي الأولوية لتقليل المتبقي الثاني قبل الأول.
تعديل المربعات الصغرى
يتكون تركيب نموذج الانحدار باستخدام معيار المربعات الصغرى من إيجاد نموذج انحدار يقلل من مربعات القيم المتبقية. ولذلك فإن المعادلة التي تم الحصول عليها من نموذج الانحدار ستكون تلك التي تكون مربعات الفروق بين القيم المرصودة والقيم المجهزة فيها ضئيلة.
لاحظ في المثال التالي أن هناك المزيد من المعايير لإنشاء نموذج الانحدار، واعتمادًا على المعيار المختار، تختلف معادلة الانحدار.
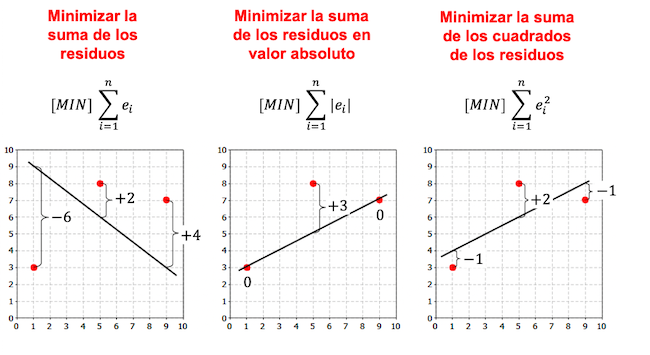
كما ترون في الأمثلة السابقة، فإن الخط الذي تم الحصول عليه من نموذج الانحدار الخطي لنفس مجموعة البيانات يعتمد على المعيار المختار. بشكل عام، يتم استخدام معيار المربعات الصغرى في نماذج الانحدار.
في الإحصاء، نموذج الانحدار الأكثر استخدامًا هو نموذج الانحدار الخطي البسيط، والذي يتكون من تقريب العلاقة بين المتغير المستقل X والمتغير التابع Y باستخدام خط مستقيم.
![]()
لذلك، فإن الصيغ الخاصة بملاءمة مجموعة البيانات مع نموذج الانحدار الخطي البسيط هي:

![]()
ويمكنكم مشاهدة مثال لكيفية حساب نموذج الانحدار الخطي البسيط باستخدام معيار المربعات الصغرى بالضغط على الرابط التالي: