كيفية إجراء انحدار المربعات الصغرى المرجحة في r

أحد الافتراضات الرئيسية للانحدار الخطي هو أن البقايا يتم توزيعها بتباين متساوي عند كل مستوى من متغير التوقع. يُعرف هذا الافتراض بالمثلية الجنسية .

عندما لا يتم احترام هذا الافتراض، يقال أن التغايرية موجودة في البقايا. عندما يحدث هذا، تصبح نتائج الانحدار غير موثوقة.

إحدى طرق حل هذه المشكلة هي استخدام انحدار المربعات الصغرى المرجحة ، والذي يعين أوزانًا للملاحظات بحيث تتلقى تلك ذات تباين الخطأ المنخفض وزنًا أكبر لأنها تحتوي على معلومات أكثر مقارنة بالملاحظات ذات تباين الخطأ الأكبر.

يوفر هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية إجراء انحدار المربعات الصغرى المرجحة في R.

الخطوة 1: إنشاء البيانات

يقوم الكود التالي بإنشاء إطار بيانات يحتوي على عدد الساعات المدروسة ودرجة الامتحان المقابلة لـ 16 طالبًا:

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

الخطوة 2: تنفيذ الانحدار الخطي

بعد ذلك، سنستخدم الدالة lm() ‎ لتناسب نموذج الانحدار الخطي البسيط الذي يستخدم الساعات كمتغير متوقع والنتيجة كمتغير الاستجابة :

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

الخطوة 3: اختبار التغايرية

بعد ذلك، سنقوم بإنشاء مخطط للقيم المتبقية والقيم المجهزة للتحقق بصريًا من عدم التجانس:

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

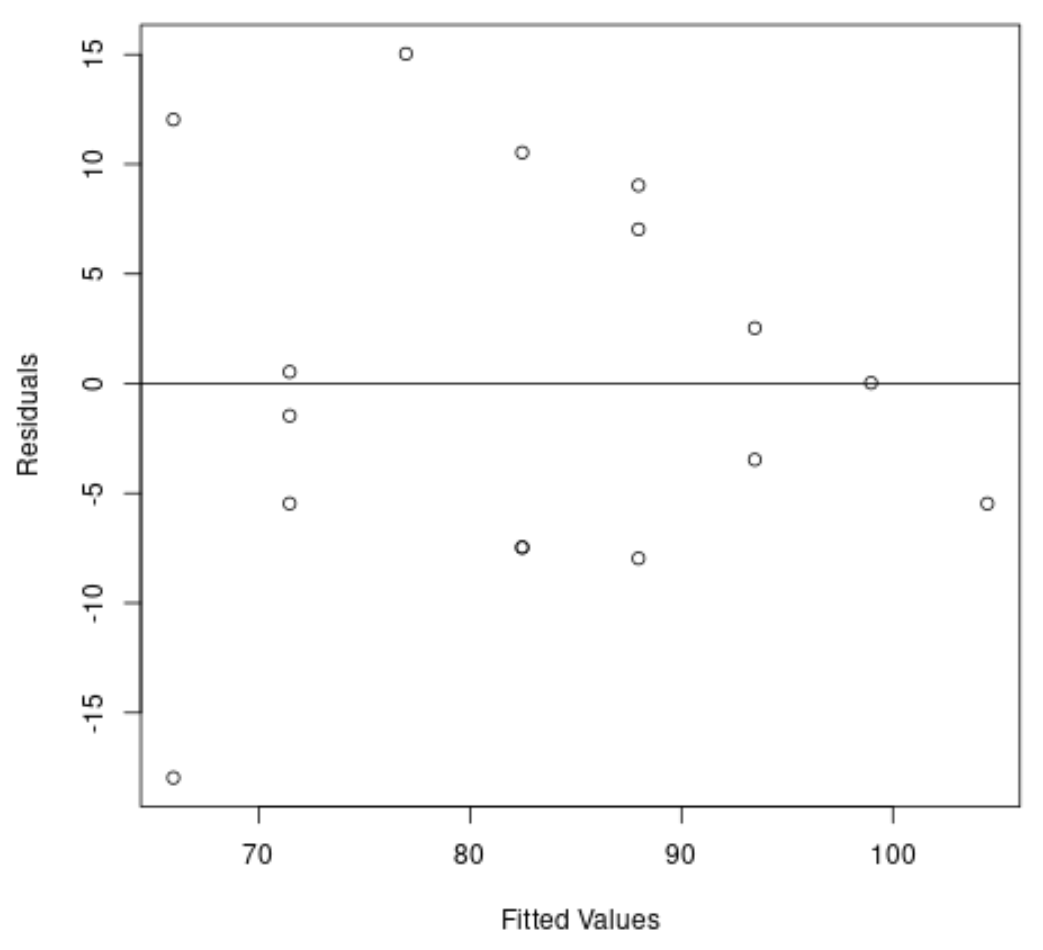
يمكننا أن نرى من الرسم البياني أن البقايا لها شكل “مخروطي”: فهي غير موزعة بتباين متساوٍ في جميع أنحاء الرسم البياني.

لاختبار التغايرية بشكل رسمي، يمكننا إجراء اختبار بروش-باغان:

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

يستخدم اختبار Breusch-Pagan الفرضيات الصفرية والبديلة التالية :

• الفرضية الصفرية (H ₀ ): التماثل موجود (يتم توزيع البقايا بتباين متساوي)
• الفرضية البديلة ( _HA ): وجود التغايرية (لا يتم توزيع البقايا بتباين متساوي)

نظرًا لأن القيمة p للاختبار هي 0.0466 ، فسوف نرفض فرضية العدم ونستنتج أن التغايرية تمثل مشكلة في هذا النموذج.

الخطوة 4: إجراء انحدار المربعات الصغرى المرجحة

نظرًا لوجود التغايرية، فسوف نقوم بإجراء المربعات الصغرى الموزونة عن طريق تعيين الأوزان بحيث تتلقى الملاحظات ذات التباين الأقل وزنًا أكبر:

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

من النتائج، يمكننا أن نرى أن تقدير المعامل لمتغير توقع الساعات قد تغير قليلاً وأن النموذج العام قد تحسن.

يحتوي نموذج المربعات الصغرى الموزونة على خطأ معياري متبقي قدره 1.199 ، مقارنة بـ 9.224 في نموذج الانحدار الخطي البسيط الأصلي.

ويشير ذلك إلى أن القيم المتوقعة التي ينتجها نموذج المربعات الصغرى الموزونة أقرب بكثير إلى الملاحظات الفعلية مقارنة بالقيم المتوقعة التي ينتجها نموذج الانحدار الخطي البسيط.

يحتوي نموذج المربعات الصغرى الموزونة أيضًا على R-squared بقيمة 0.6762 ، مقارنة بـ 0.6296 في نموذج الانحدار الخطي البسيط الأصلي.

يشير هذا إلى أن نموذج المربعات الصغرى المرجحة قادر على تفسير التباين في درجات الامتحانات أكثر من نموذج الانحدار الخطي البسيط.

تشير هذه القياسات إلى أن نموذج المربعات الصغرى المرجحة يوفر ملاءمة أفضل للبيانات مقارنة بنموذج الانحدار الخطي البسيط.

مصادر إضافية

كيفية إجراء الانحدار الخطي البسيط في R
كيفية إجراء الانحدار الخطي المتعدد في R
كيفية إجراء الانحدار الكمي في R