كيفية حساب مسافة كوك في بايثون

تُستخدم مسافة كوك لتحديد الملاحظات المؤثرة في نموذج الانحدار.

صيغة مسافة كوك هي:

د _i = (r _i ² / p*MSE) * (h _ii / (1-h _ii ) ² )

ذهب:

• r _i هو i ^{البقايا}
• p هو عدد المعاملات في نموذج الانحدار
• MSE هو متوسط الخطأ المربع
• hii _هي قيمة الرافعة ^{المالية}

بشكل أساسي، تقيس مسافة كوك مدى تغير جميع القيم المجهزة للنموذج عند إزالة الملاحظة ⁱ .

كلما كانت قيمة مسافة كوك أكبر، كلما كانت الملاحظة المعطاة أكثر تأثيرًا.

كقاعدة عامة، أي ملاحظة بمسافة كوك أكبر من 4/n (حيث n = إجمالي الملاحظات) تعتبر ذات تأثير كبير.

يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية حساب مسافة كوك لنموذج انحدار معين في بايثون.

الخطوة 1: أدخل البيانات

أولاً، سنقوم بإنشاء مجموعة بيانات صغيرة للعمل عليها في بايثون:

 import pandas as pd

#create dataset
df = pd. DataFrame ({' x ': [8, 12, 12, 13, 14, 16, 17, 22, 24, 26, 29, 30],
                   ' y ': [41, 42, 39, 37, 35, 39, 45, 46, 39, 49, 55, 57]})

الخطوة 2: تناسب نموذج الانحدار

بعد ذلك، سوف نقوم بتركيب نموذج الانحدار الخطي البسيط :

 import statsmodels. api as sm

#define response variable
y = df[' y ']

#define explanatory variable
x = df[' x ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

الخطوة 3: حساب مسافة الطهي

بعد ذلك، سوف نقوم بحساب مسافة كوك لكل ملاحظة في النموذج:

 #suppress scientific notation
import numpy as np
n.p. set_printoptions (suppress= True )

#create instance of influence
influence = model. get_influence ()

#obtain Cook's distance for each observation
cooks = influence. cooks_distance

#display Cook's distances
print (cooks)

(array([0.368, 0.061, 0.001, 0.028, 0.105, 0.022, 0.017, 0. , 0.343,
        0. , 0.15 , 0.349]),
 array([0.701, 0.941, 0.999, 0.973, 0.901, 0.979, 0.983, 1. , 0.718,
        1. , 0.863, 0.713]))

افتراضيًا، تعرض الدالة Cooks_distance() مصفوفة من القيم لمسافة Cook لكل ملاحظة متبوعة بمصفوفة من القيم p المقابلة.

على سبيل المثال:

• مسافة كوك للملاحظة رقم 1: 0.368 (قيمة p: 0.701)
• مسافة كوك للملاحظة رقم 2: 0.061 (قيمة p: 0.941)
• مسافة كوك للملاحظة رقم 3: 0.001 (قيمة p: 0.999)

وما إلى ذلك وهلم جرا.

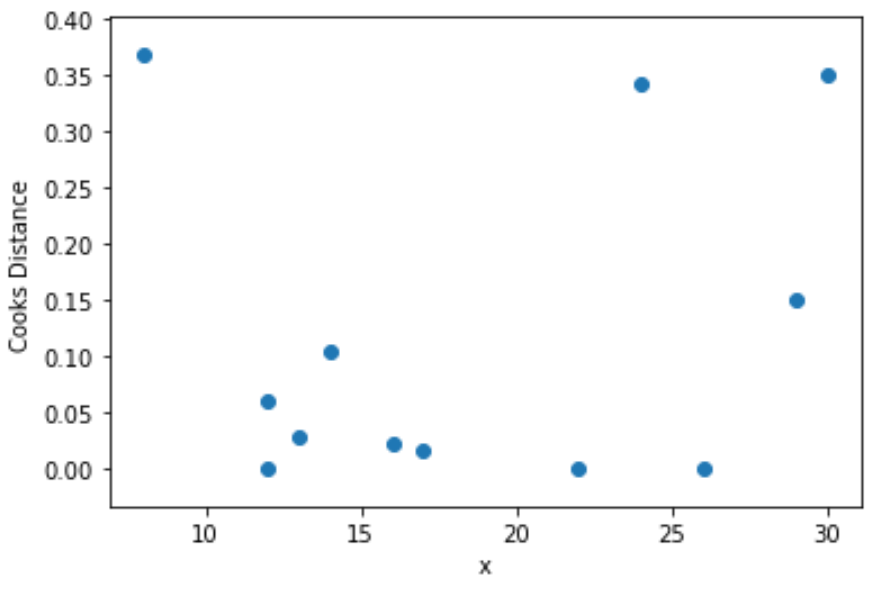
الخطوة 4: تصور مسافات الطباخ

أخيرًا، يمكننا إنشاء مخطط تشتت لتصور قيم متغير التوقع كدالة لمسافة كوك لكل ملاحظة:

 import matplotlib. pyplot as plt

plt. scatter (df.x, cooks[0])
plt. xlabel (' x ')
plt. ylabel (' Cooks Distance ')
plt. show () 

افكار اخيرة

ومن المهم أن نلاحظ أنه ينبغي استخدام مسافة كوك لتحديد الملاحظات التي يحتمل أن تكون مؤثرة. فقط لأن الملاحظة مؤثرة لا يعني أنه يجب إزالتها من مجموعة البيانات.

أولاً، عليك التحقق من أن الملاحظة ليست نتيجة خطأ في إدخال البيانات أو أي حدث غريب آخر. إذا تبين أنها قيمة مشروعة، فيمكنك بعد ذلك أن تقرر ما إذا كان من المناسب إزالتها، أو تركها كما هي، أو ببساطة استبدالها بقيمة بديلة مثل الوسيط.