كيفية تفسير المقياس ومؤامرة الموقع: مع الأمثلة

مخطط الموقع المقياس هو نوع من المخططات التي تعرض القيم المجهزة لنموذج الانحدار على طول المحور السيني والجذر التربيعي للبقايا الموحدة على طول المحور الصادي.

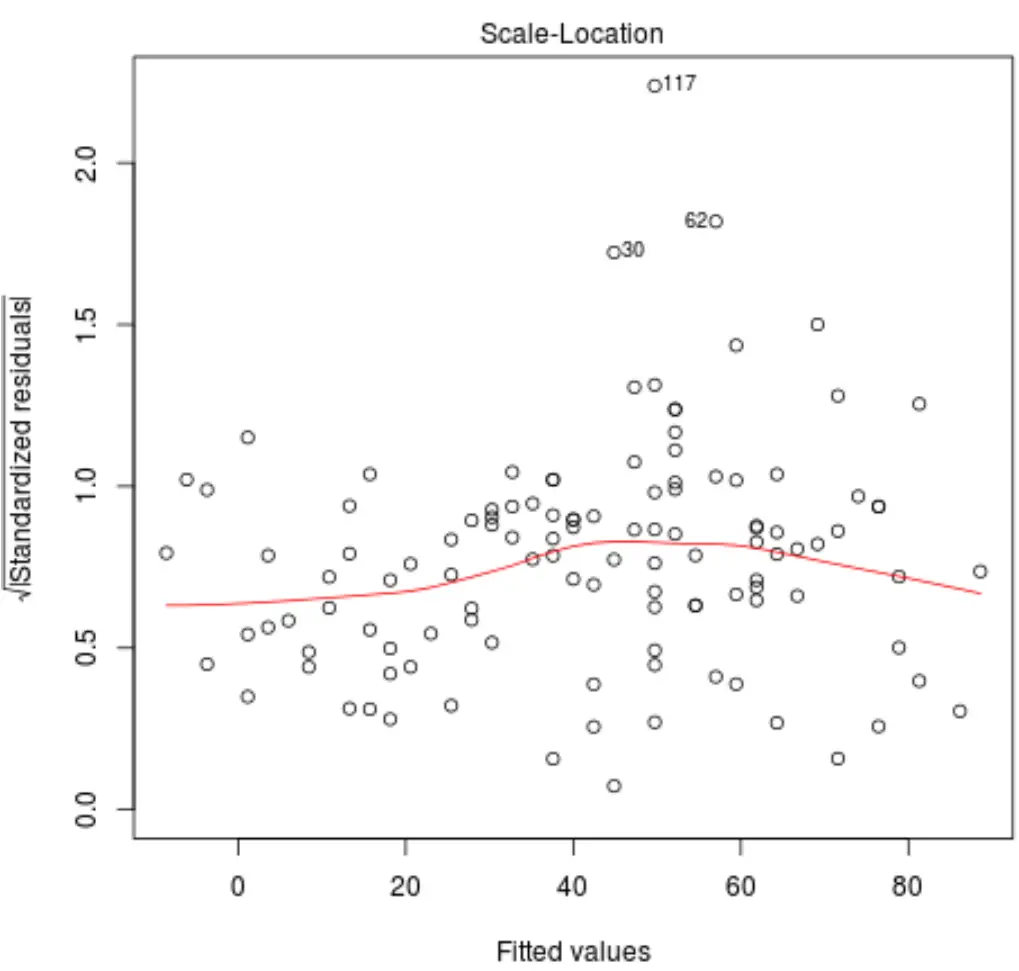
وبالنظر إلى هذا الرسم البياني، نتحقق من أمرين:

1. تأكد من أن الخط الأحمر أفقي تقريبًا على قطعة الأرض. إذا كان هذا هو الحال، فمن المحتمل أن يكون افتراض المثلية محققًا لنموذج انحدار معين. أي أن توزيع البقايا متساوي تقريبًا لجميع القيم المجهزة.

2. التأكد من عدم وجود اتجاه واضح بين المخلفات. وبعبارة أخرى، ينبغي أن تكون البقايا منتشرة بشكل عشوائي حول الخط الأحمر مع تباين متساو تقريبا لجميع القيم المجهزة.

رسم النطاق والموقع في R

يمكننا استخدام الكود التالي لملاءمة نموذج الانحدار الخطي البسيط في R وإنتاج مخطط مقياس وموقع للنموذج الناتج:

 #fit simple linear regression model
model <- lm(Ozone ~ Temp, data = airquality)

#produce scale-location plot
plot(model)

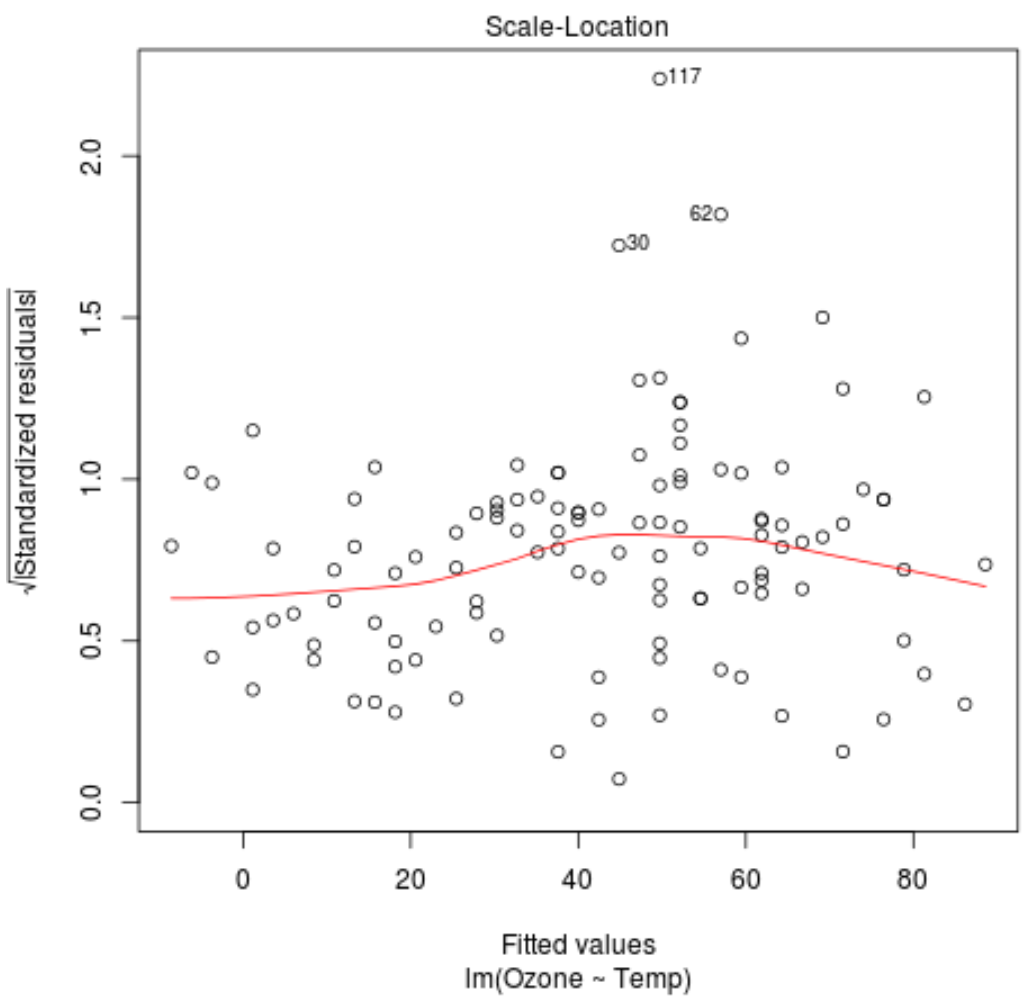
يمكننا ملاحظة الأمرين التاليين من مخطط النطاق والموقع لنموذج الانحدار هذا.

1. الخط الأحمر أفقي تقريبًا على قطعة الأرض. إذا كان هذا هو الحال، فإن افتراض المثلية يتم استيفاءه لنموذج انحدار معين. أي أن توزيع البقايا متساوي تقريبًا لجميع القيم المجهزة.

2. التأكد من عدم وجود اتجاه واضح بين المخلفات. وبعبارة أخرى، ينبغي أن تكون البقايا منتشرة بشكل عشوائي حول الخط الأحمر مع تباين متساو تقريبا لجميع القيم المجهزة.

الملاحظات الفنية

تم تصنيف الملاحظات الثلاث من مجموعة البيانات ذات أعلى المخلفات الموحدة في الرسم البياني.

يمكننا أن نرى أن الملاحظات في الأسطر 30 و62 و117 لها أعلى المخلفات المعيارية.

هذا لا يعني بالضرورة أن هذه الملاحظات هي قيم متطرفة، ولكن قد ترغب في إلقاء نظرة على البيانات الأصلية لفحص هذه الملاحظات عن كثب.

على الرغم من أننا نستطيع أن نرى أن الخط الأحمر أفقي تقريبًا على مخطط موقع المقياس، إلا أن هذا يعمل فقط كطريقة مرئية لمعرفة ما إذا كان افتراض المثلية قد تحقق أم لا.

الاختبار الإحصائي الرسمي الذي يمكننا استخدامه لمعرفة ما إذا كان افتراض المثلية قد تم استيفاءه هو اختبار بروش باغان .

اختبار Breusch-Pagan في R

يوضح التعليمة البرمجية التالية كيفية استخدام وظيفة bptest () لحزمة lmtest لإجراء اختبار Breusch-Pagan في R:

 #load lmtest package
library(lmtest)

#perform Breusch-Pagan Test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 1.4798, df = 1, p-value = 0.2238

يستخدم اختبار Breusch-Pagan الفرضيات الصفرية والبديلة التالية:

• الفرضية الصفرية (H ₀ ): البقايا متجانسة (أي موزعة بشكل موحد)
• الفرضية البديلة ( _HA ): البقايا متغايرة (أي غير موزعة بشكل موحد)

من النتيجة يمكننا أن نرى أن القيمة p للاختبار هي 0.2238 . وبما أن هذه القيمة p لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم. ليس لدينا ما يكفي من الأدلة للادعاء بأن التغايرية موجودة في نموذج الانحدار.

تتطابق هذه النتيجة مع فحصنا البصري للخط الأحمر في مخطط موقع المقياس.

مصادر إضافية

فهم التغايرية في تحليل الانحدار
كيفية إنشاء قطعة أرض متبقية في R
كيفية إجراء اختبار Breusch-Pagan في R