الموضة (إحصائيات)
تشرح هذه المقالة الوضع الموجود في الإحصائيات. سوف تتعلم كيفية العثور على الوضع الإحصائي للبيانات المجمعة والبيانات غير المجمعة، وأنواع الأوضاع المختلفة، والعديد من الأمثلة على هذا المقياس الإحصائي.
ما هو الوضع في الإحصاء؟
في الإحصائيات، الوضع هو القيمة الموجودة في مجموعة البيانات التي لها أعلى تكرار مطلق، أي أن الوضع هو القيمة الأكثر تكرارًا في مجموعة البيانات.
لذلك، لحساب وضع مجموعة البيانات الإحصائية، ما عليك سوى حساب عدد المرات التي يظهر فيها كل عنصر بيانات في العينة، وستكون البيانات الأكثر تكرارًا هي الوضع.
يُستخدم الوضع لتحديد التوزيع الإحصائي، نظرًا لأن القيمة الأكثر تكرارًا تكون عادةً في مركز التوزيع.
يمكن أيضًا القول أن الوضع هو الوضع الإحصائي أو القيمة المشروطة . وبالمثل، عندما يتم تجميع البيانات في فواصل زمنية، فإن الفاصل الزمني الأكثر تكرارًا هو الفاصل المشروط أو الفئة المشروطة .
بشكل عام، يتم استخدام المصطلح Mo كرمز للوضع الإحصائي، على سبيل المثال، وضع التوزيع X هو Mo(X).
ضع في اعتبارك أن الوضع هو مقياس إحصائي للموضع المركزي، بالإضافة إلى المتوسط والمتوسط. أدناه سنرى ما يعنيه كل من هذه التدابير الإحصائية.
أنواع الوضع في الإحصائيات
في الإحصاء، هناك عدة أنواع من الأوضاع التي يتم تصنيفها وفقًا لعدد القيم الأكثر تكرارًا:
- الوضع الأحادي : هناك قيمة واحدة فقط مع الحد الأقصى لعدد التكرارات. على سبيل المثال، [1، 4، 2، 4، 5، 3].
- الوضع ثنائي الوضع : الحد الأقصى لعدد التكرارات يحدث عند قيمتين مختلفتين، ويتم تكرار كلا القيمتين بنفس عدد المرات. على سبيل المثال، [2، 6، 7، 2، 3، 6، 9].
- الوضع المتعدد الوسائط : ثلاث قيم أو أكثر لها نفس الحد الأقصى لعدد التكرارات. على سبيل المثال، [3، 3، 4، 1، 3، 4، 2، 1، 4، 5، 2، 1].
كيفية العثور على الوضع الإحصائي
للعثور على الوضع الإحصائي لمجموعة البيانات، يجب عليك اتباع الخطوات التالية:
- ضع البيانات بالترتيب. هذه الخطوة ليست إلزامية، ولكنها ستجعل عملية عد الأرقام أسهل.
- حساب عدد المرات التي يظهر فيها كل رقم.
- الرقم الذي يظهر في أغلب الأحيان هو الوضع الإحصائي.
أمثلة على الوضع الإحصائي
بالنظر إلى تعريف الموضة في الإحصائيات، يمكنك أدناه رؤية مثال لكل نوع من أنواع الموضة حتى تتمكن من فهم المفهوم بشكل أفضل.
مثال على الوضع الأحادي
- ما هو وضع مجموعة البيانات التالية؟
![]()
الأرقام غير مرتبة، لذا سنقوم بترتيبها أولاً لتسهيل العثور على الوضع.
![]()
الرقمان 2 و 9 يظهران مرتين، لكن الرقم 5 يتكرر ثلاث مرات. ولذلك، فإن وضع سلسلة البيانات هو رقم 5.
![]()
مثال على الوضع الثنائي
- احسب وضع مجموعة البيانات التالية:
![]()
![]()
أولا نقوم بترتيب الأرقام:
![]()
![]()
كما ترى فإن الرقم 6 والرقم 8 يظهران أربع مرات إجمالاً، وهو الحد الأقصى لعدد التكرارات. ولذلك، فهو في هذه الحالة وضع ثنائي والرقمين هما وضع مجموعة البيانات:
![]()
مثال على الوضع المتعدد الوسائط
- ابحث عن وضع مجموعة البيانات التالي:
![]()
![]()
![]()
نظرًا لوجود الكثير من البيانات، نقوم أولاً بفرزها بترتيب تصاعدي لتسهيل عدها:
![]()
![]()
![]()
الأرقام الأكثر تكرارًا هي 20 و27 و31، وجميع الأرقام الثلاثة تتكرر خمس مرات. وبالتالي فإن وضع هذا المثال متعدد الوسائط.
![]()
حاسبة الموضة
أدخل البيانات من أي عينة إحصائية في الآلة الحاسبة الإلكترونية التالية لحساب وضعها. يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.
وضع للبيانات المجمعة
عندما يكون لدينا بيانات مجمعة في شكل فترات زمنية، فإننا لا نعرف حقًا عدد المرات التي يتم فيها تكرار كل جزء من البيانات، فنحن نعرف فقط تكرار كل فترة زمنية.
وبالتالي، لحساب نمط البيانات المجمعة في فترات، يجب علينا استخدام الصيغة التالية :
![]()
ذهب:
- L i هو الحد الأدنى للفاصل المشروط (أعلى فاصل ترددي مطلق).
- f i هو التكرار المطلق للفاصل المشروط.
- f i-1 هو التكرار المطلق للفاصل الزمني قبل الشكل.
- f i+1 هو التكرار المطلق للفاصل الزمني بعد الشكل.
- A i هو عرض الفاصل الزمني المشروط.
على سبيل المثال، لقد قمت أدناه بحل تمرين يتم من خلاله حساب نمط البيانات المجمعة في فترات:
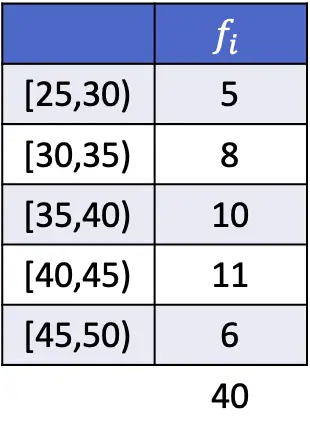
في هذه الحالة، يكون الفاصل الزمني [40,45]، لأنه الفاصل ذو أكبر تكرار مطلق. ولذلك، فإن معلمات صيغة الوضع للبيانات المجمعة هي:
![Rendered by QuickLaTeX.com \begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-85aef7092d3e0c7769ad17b96aae294c_l3.png)
ولذلك فإننا نطبق الصيغة لتحديد وضع البيانات المجمعة في فترات ونقوم بالحساب:
![Rendered by QuickLaTeX.com \begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ee33fdb43267fdcfc6d222ed6798fca_l3.png)
الفرق بين المنوال والمتوسط والوسيط
في هذا القسم الأخير سنرى ما هو الفرق بين المنوال والمتوسط والوسيط. وبما أن الثلاثة كلها عبارة عن مقاييس إحصائية للموقع المركزي، فإن معناها مختلف.
كما هو موضح في المقالة، المنوال في الرياضيات هو القيمة الأكثر تكرارًا في مجموعة البيانات.
ثانيا، المتوسط هو متوسط قيمة جميع البيانات الإحصائية. وبالتالي، للحصول على متوسط بيانات معينة، يجب عليك جمع جميع البيانات ثم قسمة النتيجة على عدد الملاحظات.
وأخيرًا، الوسيط هو القيمة التي تحتل الموضع المركزي عند ترتيب البيانات.
وبالتالي فإن المقاييس الإحصائية الثلاثة تساعد في تحديد التوزيع الاحتمالي، لأنها تقدم فكرة عن قيمه المركزية. لكن ضع في اعتبارك أنه لا يوجد مقياس أفضل من الآخر، بل يقصدون فقط مفاهيم مختلفة.
خصائص الموضة
خصائص الموضة هي:
- يمكن العثور على الوضع في كل من المتغيرات الكمية والمتغيرات النوعية.
- إذا طبقنا تحويلاً خطيًا على متغير عشوائي، فإن قيمة الوسط ستتغير اعتمادًا على العمليات المطبقة.
- بشكل عام، الوضع غير حساس للقيم المتطرفة.
- إذا كانت جميع القيم لها نفس التردد، فلا يوجد وضع.
![]()