كيفية إجراء انحدار الخط في r (مع مثال)

الانحدار الخطي هو نوع من الانحدار يستخدم عندما تكون هناك نقاط أو “عقد” حيث يتغير النمط في البيانات بشكل مفاجئ ولا يكون الانحدار الخطي والانحدار متعدد الحدود مرنين بما يكفي لملاءمة البيانات.

يوضح المثال التالي خطوة بخطوة كيفية إجراء انحدار الشريحة في R.

الخطوة 1: إنشاء البيانات

أولاً، لنقم بإنشاء مجموعة بيانات في لغة R تحتوي على متغيرين وننشئ مخططًا مبعثرًا لتصور العلاقة بين المتغيرات:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

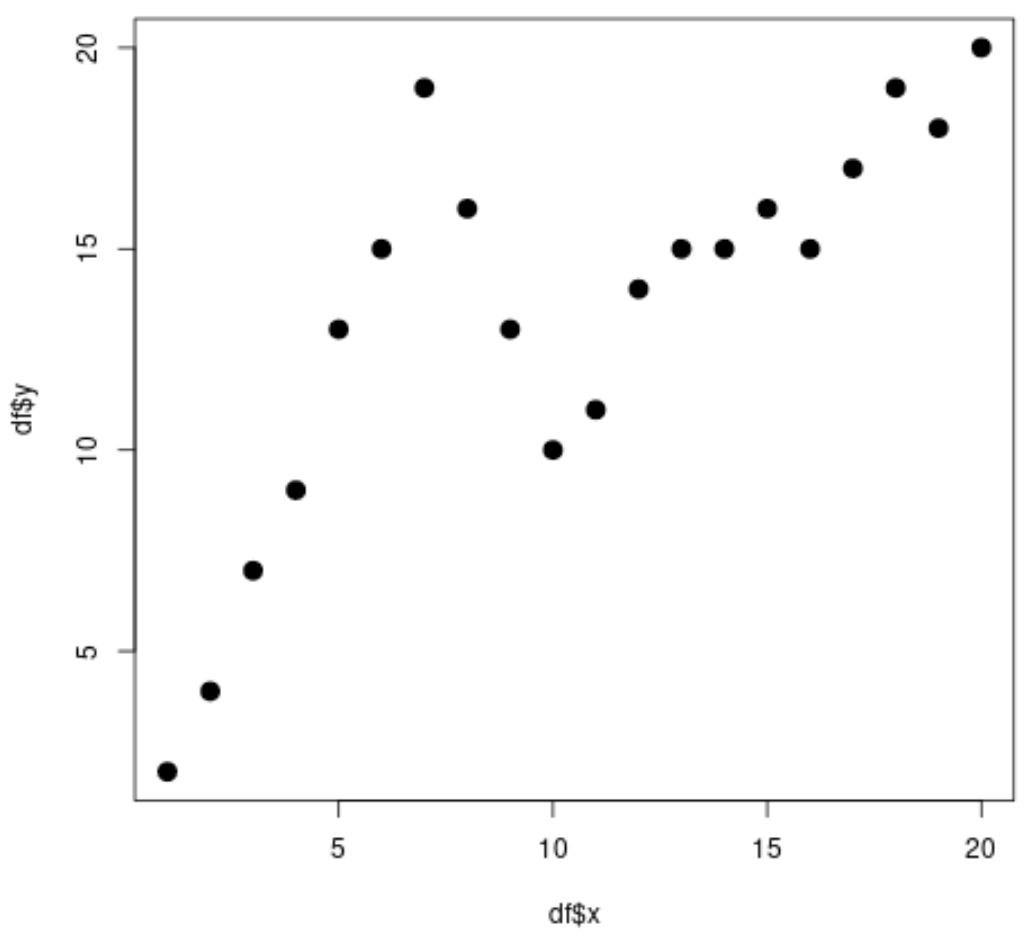
من الواضح أن العلاقة بين x وy غير خطية ويبدو أن هناك نقطتين أو “عقدتين” حيث يتغير النمط في البيانات فجأة عند x=7 وx=10.

الخطوة 2: تناسب نموذج الانحدار الخطي البسيط

لنستخدم بعد ذلك الدالة lm() ‎ لملاءمة نموذج انحدار خطي بسيط لمجموعة البيانات هذه ورسم خط الانحدار على مخطط التشتت:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

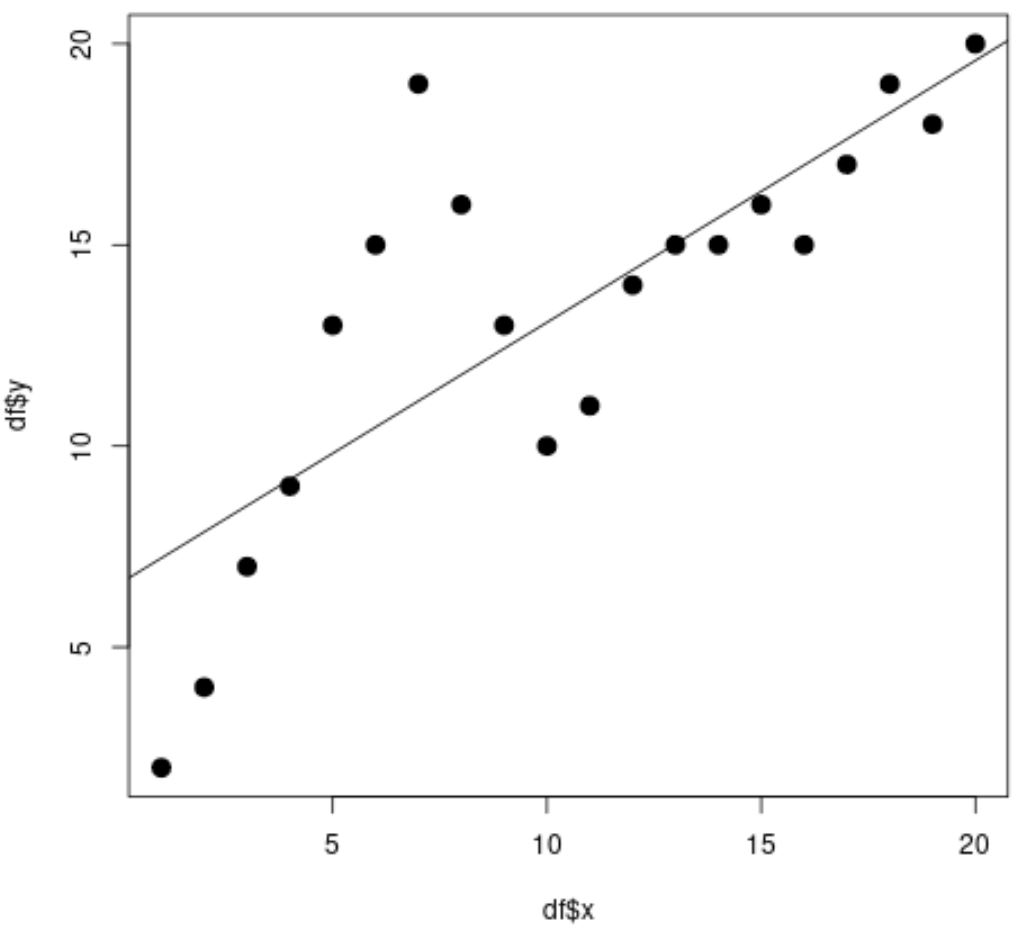
من مخطط التشتت، يمكننا أن نرى أن خط الانحدار الخطي البسيط لا يناسب البيانات بشكل جيد.

من نتائج النموذج، يمكننا أيضًا أن نرى أن قيمة R-squared المعدلة هي 0.5903 .

سنقوم بمقارنة ذلك بقيمة R-squared المعدلة لنموذج الشريحة.

الخطوة 3: ملاءمة نموذج انحدار الشريحة

بعد ذلك، دعونا نستخدم الدالة bs() ‎ من حزمة splines لملاءمة نموذج انحدار الشريحة مع عقدتين، ثم نرسم النموذج المناسب على مخطط التشتت:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

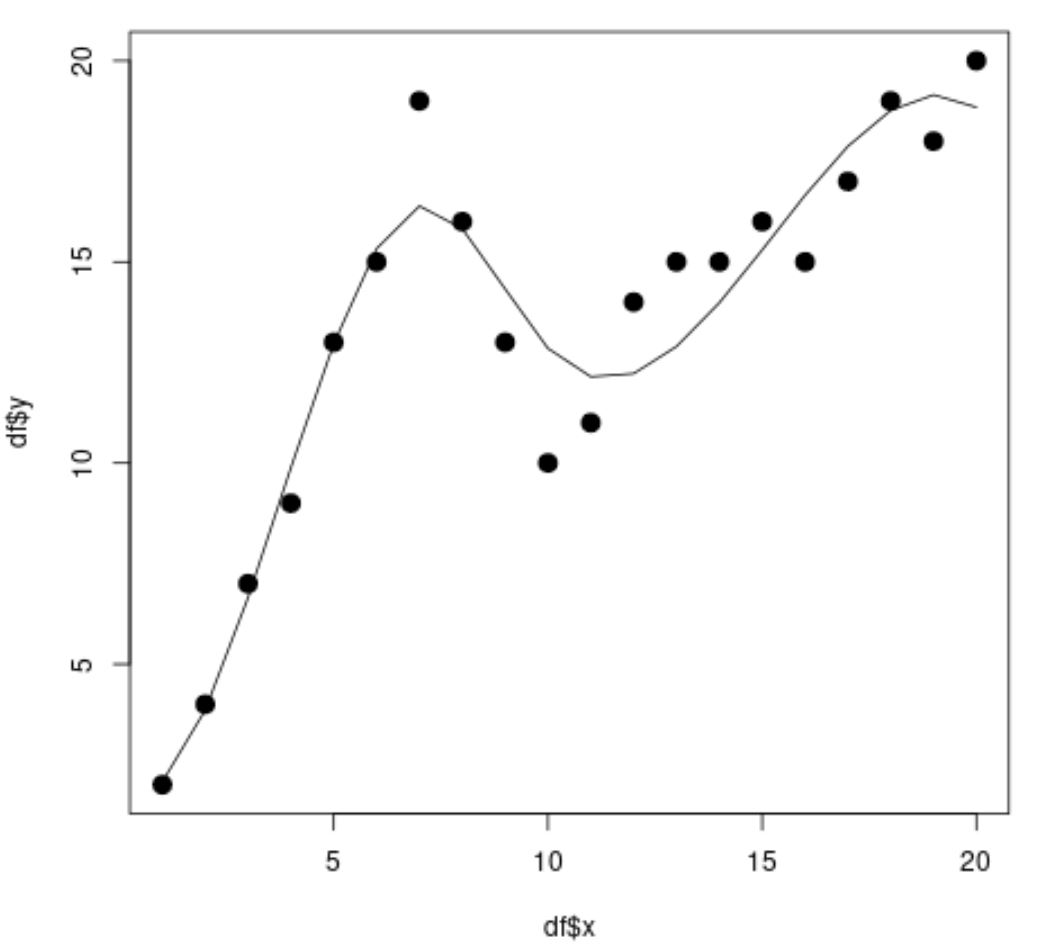
من مخطط التشتت، يمكننا أن نرى أن نموذج الانحدار الخطي قادر على ملاءمة البيانات بشكل جيد.

من نتائج النموذج، يمكننا أيضًا أن نرى أن قيمة R-squared المعدلة هي 0.8987 .

تعد قيمة R-squared المعدلة لهذا النموذج أعلى بكثير من نموذج الانحدار الخطي البسيط، مما يخبرنا أن نموذج الانحدار الخطي قادر على ملاءمة البيانات بشكل أفضل.

لاحظ أنه في هذا المثال اخترنا أن العقد تقع عند x=7 وx=10.

من الناحية العملية، ستحتاج إلى اختيار مواقع العقد بنفسك استنادًا إلى الأماكن التي يبدو أن الأنماط في البيانات تتغير فيها واستنادًا إلى خبرتك في المجال.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في R:

كيفية إجراء الانحدار الخطي المتعدد في R
كيفية إجراء الانحدار الأسي في R
كيفية إجراء انحدار المربعات الصغرى المرجحة في R