انحدار المكون الرئيسي في بايثون (خطوة بخطوة)

بالنظر إلى مجموعة من متغيرات التوقع p ومتغير الاستجابة، يستخدم الانحدار الخطي المتعدد طريقة تعرف باسم المربعات الصغرى لتقليل مجموع المربعات المتبقية (RSS):

RSS = Σ(y _i – ŷ _i ) ²

ذهب:

• Σ : رمز يوناني معناه المجموع
• y _i : قيمة الاستجابة الفعلية للملاحظة ^{رقم i}
• ŷ _i : قيمة الاستجابة المتوقعة بناءً على نموذج الانحدار الخطي المتعدد

ومع ذلك، عندما تكون متغيرات التوقع مترابطة بشكل كبير، يمكن أن تصبح العلاقة الخطية المتعددة مشكلة. وهذا يمكن أن يجعل تقديرات معامل النموذج غير موثوقة وتظهر تباينًا كبيرًا.

إحدى الطرق لتجنب هذه المشكلة هي استخدام انحدار المكونات الرئيسية ، الذي يجد مجموعات خطية M (تسمى “المكونات الرئيسية”) من تنبؤات p الأصلية ثم يستخدم المربعات الصغرى لتناسب نموذج الانحدار الخطي باستخدام المكونات الرئيسية كمتنبئات.

يقدم هذا البرنامج التعليمي مثالاً خطوة بخطوة لكيفية تنفيذ انحدار المكونات الرئيسية في بايثون.

الخطوة 1: استيراد الحزم اللازمة

أولاً، سنقوم باستيراد الحزم اللازمة لتنفيذ انحدار المكون الرئيسي (PCR) في بايثون:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn. PCA import decomposition
from sklearn. linear_model import LinearRegression
from sklearn. metrics import mean_squared_error

الخطوة 2: تحميل البيانات

في هذا المثال، سنستخدم مجموعة بيانات تسمى mtcars ، والتي تحتوي على معلومات عن 33 سيارة مختلفة. سوف نستخدم hp كمتغير الاستجابة والمتغيرات التالية كتنبؤات:

• ميلا في الغالون
• عرض
• القرف
• وزن
• com.qsec

يوضح الكود التالي كيفية تحميل مجموعة البيانات هذه وعرضها:

 #define URL where data is located
url = "https://raw.githubusercontent.com/- Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

الخطوة 3: ضبط نموذج PCR

يوضح الكود التالي كيفية ملاءمة نموذج PCR لهذه البيانات. لاحظ ما يلي:

• pca.fit_transform(scale(X)) : يخبر هذا Python أن كل متغير من متغيرات التوقع يجب أن يتم قياسه ليكون متوسطه 0 وانحرافًا معياريًا قدره 1. وهذا يضمن عدم وجود متغير توقع له تأثير كبير في النموذج إذا يحدث هذا. ليتم قياسها في وحدات مختلفة.
• cv = RepeatedKFold() : هذا يخبر Python باستخدام التحقق المتبادل k-fold لتقييم أداء النموذج. في هذا المثال نختار k = 10 أضعاف، تكرر 3 مرات.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#scale predictor variables
pca = pca()
X_reduced = pca. fit_transform ( scale (X))

#define cross validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

regr = LinearRegression()
mse = []

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (regr,
           n.p. ones ((len(X_reduced),1)), y, cv=cv,
           scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    score = -1*model_selection. cross_val_score (regr,
               X_reduced[:,:i], y, cv=cv, scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)
    
# Plot cross-validation results    
plt. plot (mse)
plt. xlabel ('Number of Principal Components')
plt. ylabel ('MSE')
plt. title ('hp') 

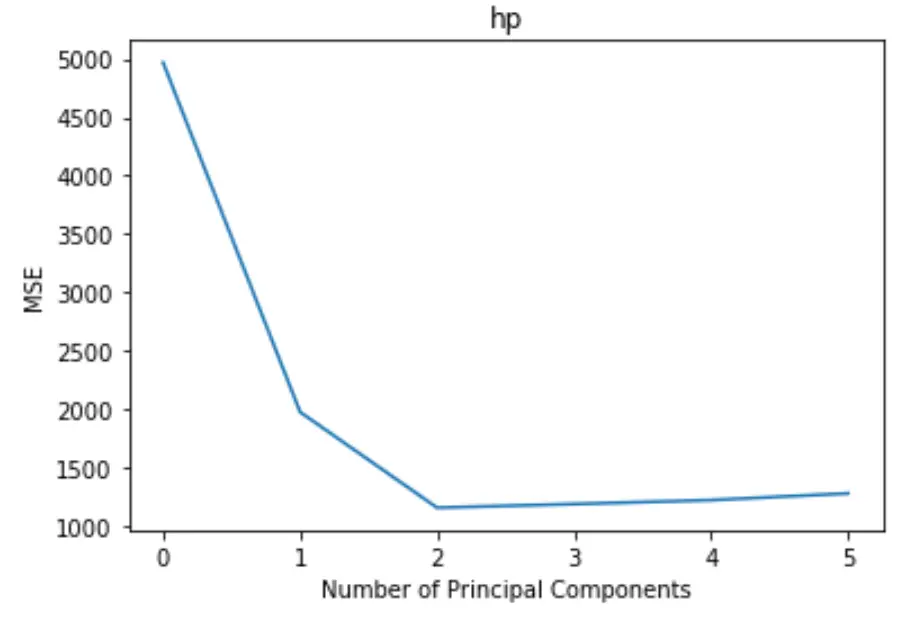
تعرض المؤامرة عدد المكونات الرئيسية على طول المحور السيني واختبار MSE (متوسط الخطأ المربع) على طول المحور الصادي.

من الرسم البياني، يمكننا أن نرى أن MSE للاختبار يتناقص بإضافة مكونين رئيسيين، لكنه يبدأ في الزيادة كلما أضفنا أكثر من مكونين رئيسيين.

وبالتالي، فإن النموذج الأمثل يشمل فقط المكونين الرئيسيين الأولين.

يمكننا أيضًا استخدام الكود التالي لحساب نسبة التباين في متغير الاستجابة الموضح بإضافة كل مكون رئيسي إلى النموذج:

 n.p. cumsum (np. round (pca. explained_variance_ratio_ , decimals= 4 )* 100 )

array([69.83, 89.35, 95.88, 98.95, 99.99])

يمكننا أن نرى ما يلي:

• وباستخدام المكون الرئيسي الأول فقط يمكننا تفسير 69.83% من التباين في متغير الاستجابة.
• وبإضافة المكون الرئيسي الثاني يمكننا تفسير 89.35% من التباين في متغير الاستجابة.

لاحظ أننا سنظل قادرين على تفسير المزيد من التباين باستخدام المزيد من المكونات الرئيسية، ولكن يمكننا أن نرى أن إضافة أكثر من مكونين رئيسيين لا يؤدي في الواقع إلى زيادة النسبة المئوية للتباين الموضح كثيرًا.

الخطوة 4: استخدم النموذج النهائي لعمل تنبؤات

يمكننا استخدام نموذج PCR النهائي المكون من عنصرين رئيسيين للتنبؤ بالملاحظات الجديدة.

يوضح الكود التالي كيفية تقسيم مجموعة البيانات الأصلية إلى مجموعة تدريب واختبار واستخدام نموذج PCR مع مكونين رئيسيين لإجراء تنبؤات على مجموعة الاختبار.

 #split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size= 0.3 , random_state= 0 ) 

#scale the training and testing data
X_reduced_train = pca. fit_transform ( scale (X_train))
X_reduced_test = pca. transform ( scale (X_test))[:,:1]

#train PCR model on training data 
regr = LinearRegression()
reg. fit (X_reduced_train[:,:1], y_train)

#calculate RMSE
pred = regr. predict (X_reduced_test)
n.p. sqrt ( mean_squared_error (y_test, pred))

40.2096

نرى أن اختبار RMSE تبين أنه 40.2096 . هذا هو متوسط الانحراف بين قيمة حصان المتوقعة وقيمة حصان المرصودة لملاحظات مجموعة الاختبار.

يمكن العثور على كود Python الكامل المستخدم في هذا المثال هنا .