انحدار لاسو في r (خطوة بخطوة)

يعد انحدار Lasso طريقة يمكننا استخدامها لتناسب نموذج الانحدار عند وجود علاقة خطية متعددة في البيانات.

باختصار، يحاول انحدار المربعات الصغرى العثور على تقديرات للمعامل تقلل من مجموع المربعات المتبقية (RSS):

RSS = Σ(ص _ط – ŷ _ط )2

ذهب:

• Σ : رمز يوناني يعني المبلغ
• y _i : قيمة الاستجابة الفعلية للملاحظة ^{رقم i}
• ŷ _i : قيمة الاستجابة المتوقعة بناءً على نموذج الانحدار الخطي المتعدد

على العكس من ذلك، يسعى انحدار اللاسو إلى تقليل ما يلي:

RSS + Σ|β _ي |

حيث تنتقل j من 1 إلى متغيرات التوقع p و ≥ ≥ 0.

يُعرف هذا الحد الثاني في المعادلة بعقوبة الانسحاب . في انحدار اللاسو، نختار قيمة π التي تنتج أقل اختبار ممكن لـ MSE (متوسط مربع الخطأ).

يوفر هذا البرنامج التعليمي مثالاً خطوة بخطوة حول كيفية إجراء انحدار لاسو في R.

الخطوة 1: تحميل البيانات

في هذا المثال، سوف نستخدم مجموعة بيانات R المضمنة والتي تسمى mtcars . سوف نستخدم hp كمتغير الاستجابة والمتغيرات التالية كتنبؤات:

• ميلا في الغالون
• وزن
• القرف
• com.qsec

لإجراء انحدار اللاسو، سوف نستخدم وظائف من حزمة glmnet . تتطلب هذه الحزمة أن يكون متغير الاستجابة متجهًا وأن تكون مجموعة متغيرات التوقع من فئة data.matrix .

يوضح الكود التالي كيفية تحديد بياناتنا:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

الخطوة 2: ملاءمة نموذج انحدار Lasso

بعد ذلك، سنستخدم الدالة glmnet() ‎ لملاءمة نموذج انحدار اللاسو وتحديد alpha=1 .

لاحظ أن تعيين ألفا يساوي 0 يعادل استخدام انحدار التلال وتعيين ألفا على قيمة بين 0 و1 يعادل استخدام شبكة مرنة.  

لتحديد القيمة التي سيتم استخدامها لامدا، سوف نقوم بإجراء التحقق من صحة k-fold وتحديد قيمة لامدا التي تنتج أدنى خطأ في متوسط مربع الاختبار (MSE).

لاحظ أن الدالة cv.glmnet() تقوم تلقائيًا بإجراء التحقق المتبادل من k-fold باستخدام k = 10 مرات.

 library (glmnet)

#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 5.616345

#produce plot of test MSE by lambda value
plot(cv_model) 

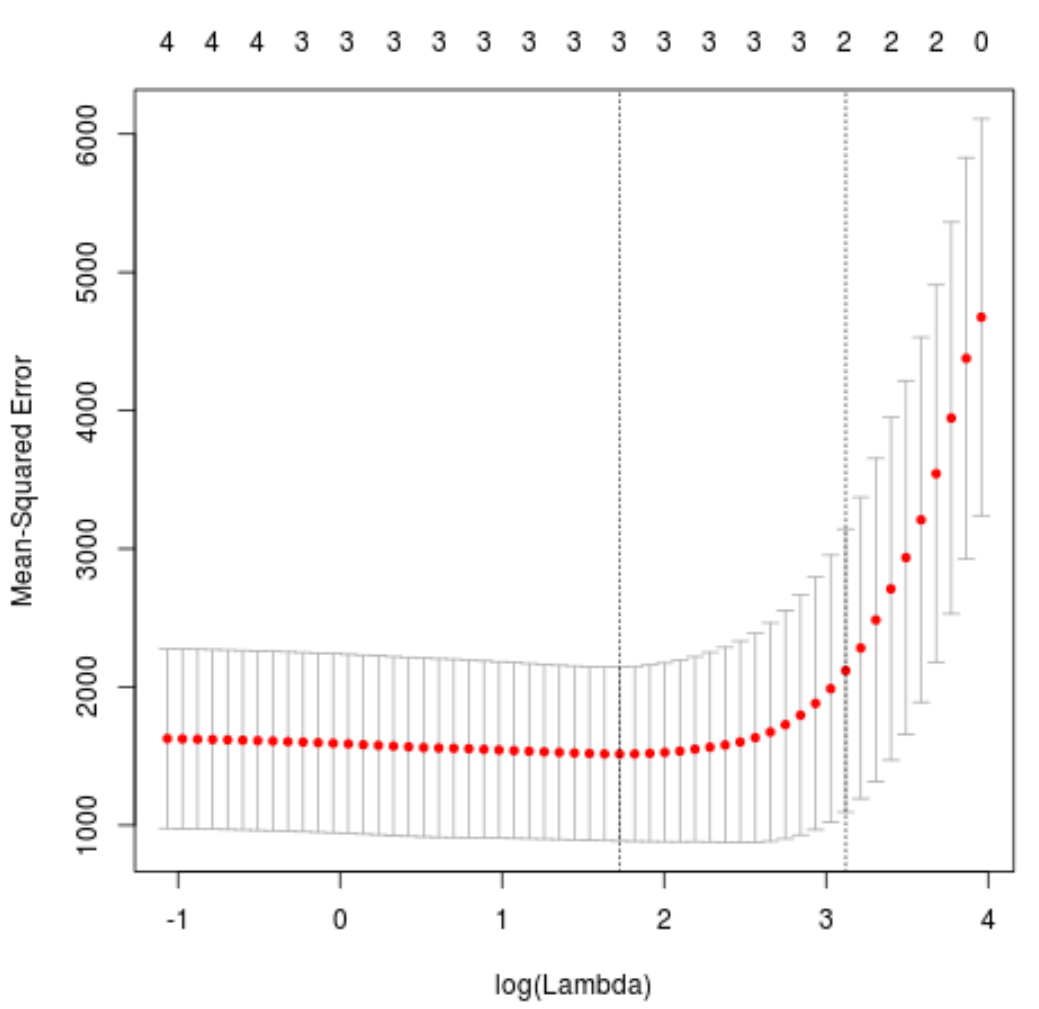
تبين أن قيمة لامدا التي تقلل من اختبار MSE هي 5.616345 .

الخطوة 3: تحليل النموذج النهائي

وأخيرا، يمكننا تحليل النموذج النهائي الناتج عن قيمة لامدا المثلى.

يمكننا استخدام الكود التالي للحصول على تقديرات المعامل لهذا النموذج:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                   s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.      
qsec -19.43425

لا يتم عرض أي معامل لمتنبئ drat لأن انحدار lasso قلل المعامل إلى الصفر. وهذا يعني أنه تمت إزالته بالكامل من النموذج لأنه لم يكن لديه التأثير الكافي.

لاحظ أن هذا هو الفرق الرئيسي بين انحدار التلال وانحدار اللاسو . يؤدي انحدار ريدج إلى تقليل جميع المعاملات نحو الصفر، ولكن انحدار لاسو لديه القدرة على إزالة المتنبئين من النموذج عن طريق تقليل المعاملات بالكامل إلى الصفر.

يمكننا أيضًا استخدام نموذج انحدار اللاسو النهائي للتنبؤ بالملاحظات الجديدة. على سبيل المثال، لنفترض أن لدينا سيارة جديدة تتمتع بالصفات التالية:

• ميلا في الغالون: 24
• الوزن: 2.5
• السعر: 3.5
• كيو سيك: 18.5

يوضح التعليمة البرمجية التالية كيفية استخدام نموذج انحدار اللاسو المُجهز للتنبؤ بقيمة HP لهذه الملاحظة الجديدة:

 #define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 ) 

#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)

[1,] 109.0842

وبناء على القيم المدخلة، يتوقع النموذج أن تبلغ قوة هذه السيارة 109.0842 حصان .

وأخيرًا، يمكننا حساب مربع R للنموذج على بيانات التدريب:

 #use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.8047064

تبين أن مربع R يساوي 0.8047064 . أي أن النموذج الأفضل استطاع تفسير 80.47% من التباين في قيم الاستجابة لبيانات التدريب.

يمكنك العثور على رمز R الكامل المستخدم في هذا المثال هنا .