كيفية حساب aic في sas (مع مثال)

يعد معيار معلومات Akaike (AIC) مقياسًا يستخدم لمقارنة ملاءمة نماذج الانحدار المتعددة.

يتم حسابه على النحو التالي:

AIC = 2K – 2 لتر (L)

ذهب:

• K: عدد معلمات النموذج. القيمة الافتراضية لـ K هي 2، وبالتالي فإن النموذج الذي يحتوي على متغير توقع واحد فقط سيكون له قيمة K هي 2+1 = 3.
• ln (L) : الاحتمالية اللوغاريتمية للنموذج. يمكن لمعظم البرامج الإحصائية حساب هذه القيمة لك تلقائيًا.

تم تصميم AIC للعثور على النموذج الذي يفسر أكبر قدر من الاختلاف في البيانات، مع معاقبة النماذج التي تستخدم عددًا مفرطًا من المعلمات.

بمجرد تركيب نماذج الانحدار المتعددة، يمكنك مقارنة قيمة AIC لكل نموذج. كلما انخفض AIC، كان النموذج أكثر ملاءمة.

يوضح المثال التالي كيفية حساب AIC لنماذج الانحدار المختلفة في SAS.

مثال: كيفية حساب AIC في SAS

لنفترض أننا نريد ملاءمة ثلاثة نماذج مختلفة للانحدار الخطي المتعدد للتنبؤ بدرجة الاختبار التي سيحققها الطلاب في الفصل الدراسي.

فيما يلي المتغيرات المتوقعة التي سنستخدمها في كل نموذج:

• المتغيرات المتنبئة في النموذج 1: الساعات المستغرقة في الدراسة
• المتغيرات التوقعية في نموذج 2: الاختبارات العملية السابقة
• المتغيرات المتوقعة في النموذج 3: الساعات التي يقضيها في الدراسة والامتحانات التدريبية التي تم إجراؤها

أولاً، سنستخدم الكود التالي لإنشاء مجموعة بيانات تحتوي على هذه المعلومات لـ 20 طالبًا:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

بعد ذلك، سوف نستخدم proc reg لملاءمة كل نموذج من نماذج الانحدار هذه وسنستخدم عبارة التحديد=adjrsq sse aic لحساب قيم AIC لكل نموذج:

 /*fit multiple linear regression models and calculate AIC for each model*/
proc reg data =exam_data;
    model score = hours prep_exams / selection=adjrsq sse aic;
run ; 

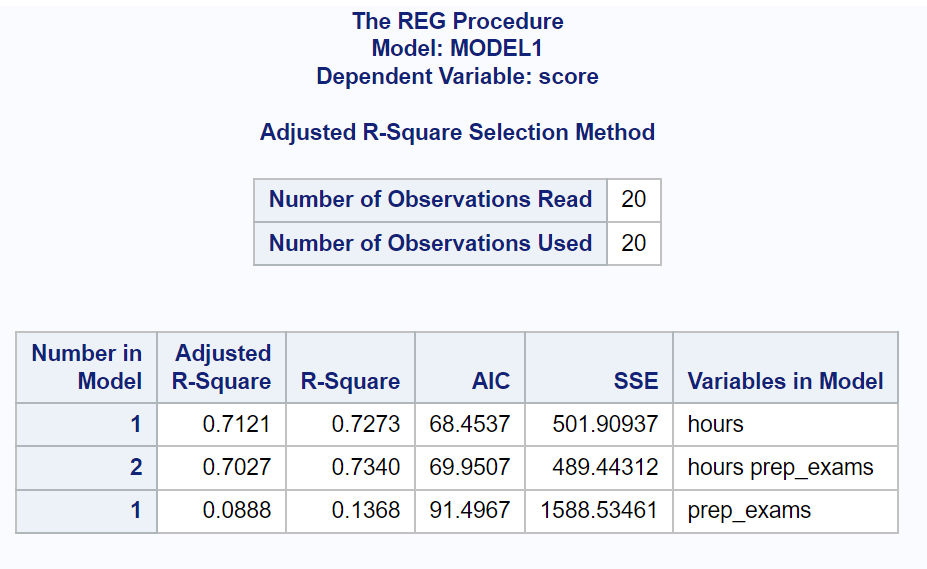
من النتيجة يمكننا رؤية قيم AIC لكل نموذج:

• AIC مع ساعات كمتغير متوقع: 68.4537
• AIC مع الساعات والامتحانات كمتغيرات متوقعة: 69.9507
• AIC مع الامتحانات كمتغير تنبؤي: 91.4967

النموذج ذو أدنى قيمة AIC هو النموذج الذي يحتوي على ساعات فقط كمتغير متوقع.

وبالتالي نعلن أن النموذج التالي يناسب البيانات بشكل أفضل:

النتيجة = β ₀ + β ₁ (ساعات الدراسة)

بمجرد تحديد هذا النموذج على أنه الأفضل، يمكننا ملاءمته وتحليل النتائج، بما في ذلك قيمة R-squared ومعاملات بيتا، لتحديد العلاقة الدقيقة بين ساعات الدراسة ودرجة الطالب. ‘إمتحان نهائي.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في SAS:

كيفية إجراء الانحدار الخطي البسيط في SAS
كيفية إجراء الانحدار الخطي المتعدد في SAS
كيفية حساب R-squared في SAS
كيفية حساب RMSE في SAS