ما هي الأحداث المنفصلة؟ (تعريف وأمثلة)

الأحداث المنفصلة هي الأحداث التي لا يمكن أن تحدث في نفس الوقت.

يكون الحدثان A و B ، المكتوبان بالترميز الاحتمالي، منفصلين إذا كانتقاطعهما صفرًا. يمكن كتابة هذا على النحو التالي:

• ف(أ وب) = 0
• ف(أ∩ب) = 0

على سبيل المثال، لنفترض أننا اخترنا بطاقة بشكل عشوائي من مجموعة البطاقات. دع الحدث A هو حدث أن البطاقة عبارة عن أشياء بأسمائها الحقيقية أو هراوة، ودع الحدث B هو حدث أن البطاقة عبارة عن قلب أو ألماسة.

ويمكننا تعريف فضاء العينة للأحداث على النحو التالي:

• أ = {الأشياء بأسمائها الحقيقية، النادي}
• ب = {القلب، الماس}

لاحظ أنه لا يوجد تداخل بين المساحتين اللتين تم أخذ عينات منهما. وبالتالي، فإن الحدثين A وB هما حدثان منفصلان لأنهما لا يمكن أن يحدثا في نفس الوقت.

ملحوظة: يقال أيضًا أن الأحداث المنفصلة متنافية .

أمثلة على الأحداث المنفصلة

فيما يلي بعض الأمثلة الإضافية للأحداث المنفصلة.

مثال 1: رسم

لنفترض أنك الوجه عملة معدنية. دع الحدث A هو الحدث الذي هبطت فيه العملة على الرؤوس، والحدث B هو الحدث الذي هبطت فيه العملة على الرؤوس.

سيكون الحدث A والحدث B منفصلين لأنه لا يمكن أن يحدث كلاهما في نفس الوقت. لا يمكن للعملة أن تهبط على الرؤوس أو الذيل.

مثال 2: رمي النرد

لنفترض أنك رميت حجر النرد. دع الحدث A هو الحدث الذي يقع فيه حجر النرد على رقم فردي، ودع الحدث B هو الحدث الذي يقع فيه حجر النرد على رقم زوجي.

سيكون الحدث A والحدث B منفصلين لأنه لا يمكن أن يحدث كلاهما في نفس الوقت. لا يمكن أن يقع حجر النرد على عدد زوجي وعلى عدد فردي.

مثال 3: موقع Pro Bowl

لنفترض أن اتحاد كرة القدم الأميركي يريد اختيار موقع لاستضافة Pro Bowl. لقد قاموا بتضييق نطاق الخيارات في ميامي وسان دييغو. يضعون الاسمين في قبعة ويختارون واحدًا عشوائيًا. لنفترض أن الحدث “أ” هو الحدث الذي اختاروا ميامي له وأن الحدث “ب” هو الحدث الذي اختاروا سان دييغو له.

سيكون الحدث A والحدث B منفصلين لأنه لا يمكن أن يحدث كلاهما في نفس الوقت. لا يمكن اختيار كل من ميامي وسان دييغو.

عرض الأحداث المنفصلة

إحدى الطرق المفيدة لتصور الأحداث المنفصلة هي إنشاء مخطط Venn.

إذا كان هناك حدثان منفصلان ، فلن يتداخلا على الإطلاق في مخطط Venn:

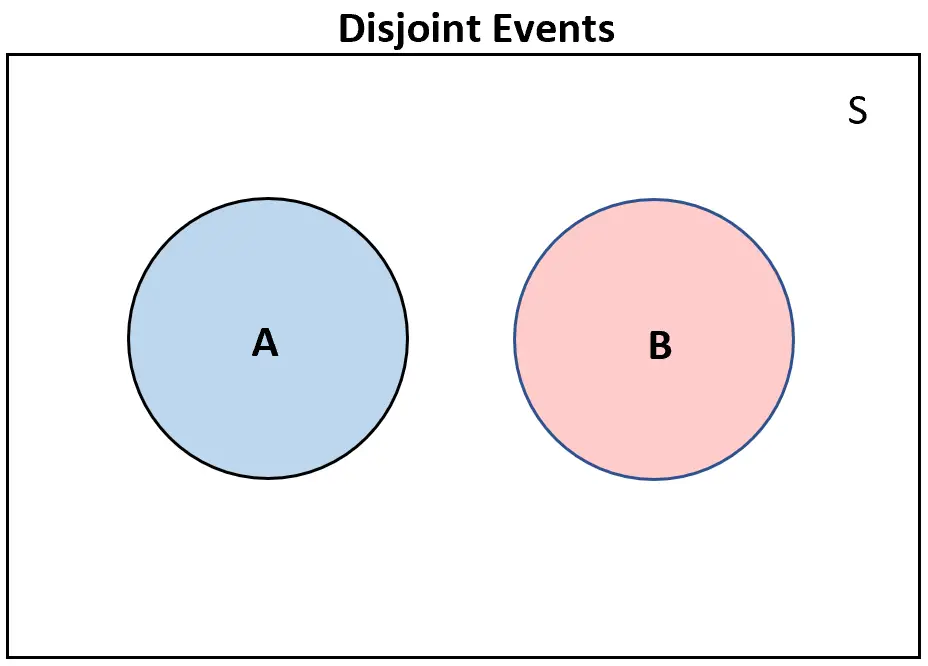
على العكس من ذلك، إذا لم يكن هناك حدثان منفصلان ، فسيكون هناك على الأقل بعض التداخل في مخطط فين:

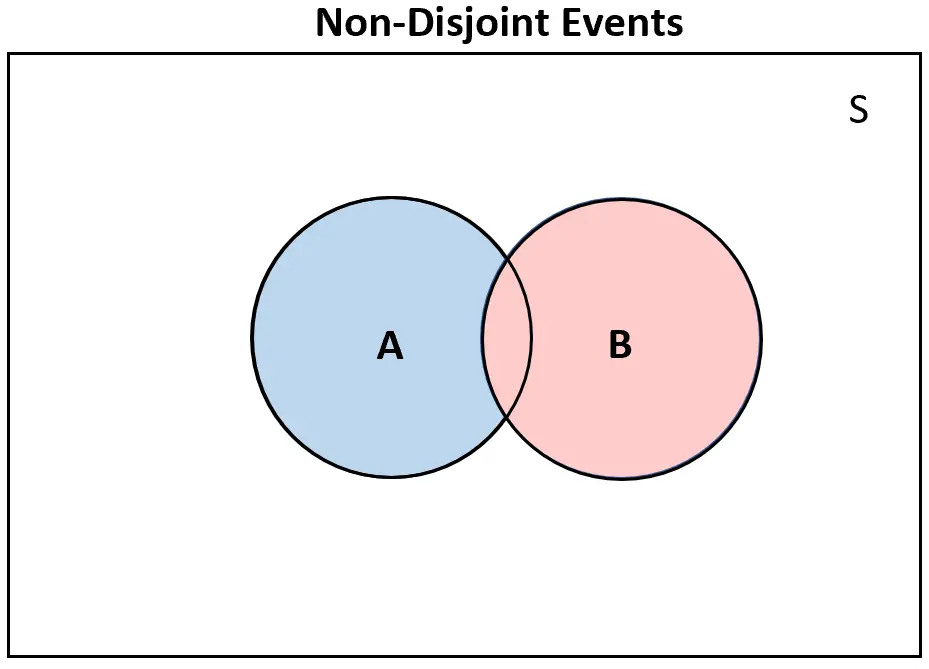
احتمال وقوع أحداث منفصلة

كما ذكرنا سابقًا، إذا كان هناك حدثان منفصلان، فإن احتمال وقوعهما في نفس الوقت هو صفر.

• ف(أ∩ب) = 0

وبالمثل، يمكن حساب احتمال وقوع أي من الحدثين عن طريق إضافة الاحتمالات الفردية لكل منهما.

• ف(أ∪ب) = ف(أ) + ف(ب)

على سبيل المثال، ليكن الحدث A هو الحدث الذي يقع فيه حجر النرد على الرقم 1 أو 2، وليكن الحدث B هو الحدث الذي يقع فيه حجر النرد على الرقم 5 أو 6.

ويمكننا تعريف فضاء العينة للأحداث على النحو التالي:

• أ = {1، 2}
• ب = {5، 6}

سنحسب احتمال وقوع الحدث A أو الحدث B على النحو التالي:

• ف(أ∪ب) = ف(أ) + ف(ب)
• ف(أ∪ب) = 2/6 + 2/6
• ف(أ∪ب) = 4/6 = 2/3

احتمال وقوع الحدث A أو الحدث B هو 2/3 .

مصادر إضافية

توفر البرامج التعليمية التالية شرحًا لموضوعات الاحتمالات الشائعة الأخرى:

كيفية العثور على احتمال A أو B: مع الأمثلة
كيفية إيجاد احتمالية A وB: مع الأمثلة
قانون الاحتمال الكلي: التعريف والأمثلة