كيفية ملاءمة أشجار التصنيف والانحدار في r

عندما تكون العلاقة بين مجموعة من المتغيرات المتوقعة ومتغير الاستجابة خطية، فإن طرق مثل الانحدار الخطي المتعدد يمكن أن تنتج نماذج تنبؤية دقيقة.

ومع ذلك، عندما تكون العلاقة بين مجموعة من التنبؤات والاستجابة أكثر تعقيدًا، يمكن للطرق غير الخطية في كثير من الأحيان إنتاج نماذج أكثر دقة.

إحدى هذه الطرق هي أشجار التصنيف والانحدار (CART)، والتي تستخدم مجموعة من المتغيرات المتوقعة لإنشاء أشجار القرار التي تتنبأ بقيمة متغير الاستجابة.

إذا كان متغير الاستجابة مستمرًا يمكننا بناء أشجار الانحدار وإذا كان متغير الاستجابة قاطعًا يمكننا بناء أشجار التصنيف.

يشرح هذا البرنامج التعليمي كيفية إنشاء أشجار الانحدار والتصنيف في R.

المثال 1: بناء شجرة الانحدار في R

في هذا المثال، سوف نستخدم مجموعة بيانات Hitters من حزمة ISLR ، والتي تحتوي على معلومات متنوعة عن 263 لاعب بيسبول محترف.

سوف نستخدم مجموعة البيانات هذه لإنشاء شجرة انحدار تستخدم المتغيرات المتوقعة لعدد مرات اللعب على أرضه وسنوات اللعب للتنبؤ براتب لاعب معين.

استخدم الخطوات التالية لإنشاء شجرة الانحدار هذه.

الخطوة 1: تحميل الحزم اللازمة.

أولاً، سنقوم بتحميل الحزم اللازمة لهذا المثال:

 library (ISLR) #contains Hitters dataset
library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

الخطوة 2: بناء شجرة الانحدار الأولية.

أولاً، سنقوم ببناء شجرة انحدار أولية كبيرة. يمكننا أن نضمن أن الشجرة كبيرة باستخدام قيمة صغيرة لـ cp ، والتي تشير إلى “معلمة التعقيد”.

هذا يعني أننا سنقوم بإجراء المزيد من الانقسامات على شجرة الانحدار طالما أن مربع R الإجمالي للنموذج يزيد على الأقل بالقيمة المحددة بواسطة cp.

سنستخدم بعد ذلك الدالة printcp() ‎ لطباعة نتائج النموذج:

 #build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error xerror xstd
1 0.24674996 0 1.00000 1.00756 0.13890
2 0.10806932 1 0.75325 0.76438 0.12828
3 0.01865610 2 0.64518 0.70295 0.12769
4 0.01761100 3 0.62652 0.70339 0.12337
5 0.01747617 4 0.60891 0.70339 0.12337
6 0.01038188 5 0.59144 0.66629 0.11817
7 0.01038065 6 0.58106 0.65697 0.11687
8 0.00731045 8 0.56029 0.67177 0.11913
9 0.00714883 9 0.55298 0.67881 0.11960
10 0.00708618 10 0.54583 0.68034 0.11988
11 0.00516285 12 0.53166 0.68427 0.11997
12 0.00445345 13 0.52650 0.68994 0.11996
13 0.00406069 14 0.52205 0.68988 0.11940
14 0.00264728 15 0.51799 0.68874 0.11916
15 0.00196586 16 0.51534 0.68638 0.12043
16 0.00016686 17 0.51337 0.67577 0.11635
17 0.00010000 18 0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

الخطوة 3: تقليم الشجرة

بعد ذلك، سنقوم بتقليم شجرة الانحدار للعثور على القيمة المثلى لاستخدامها في cp (معلمة التعقيد) التي تؤدي إلى أقل خطأ في الاختبار.

لاحظ أن القيمة المثلى لـ cp هي القيمة التي تؤدي إلى أدنى خطأ x في الإخراج السابق، والذي يمثل الخطأ في الملاحظات من بيانات التحقق من الصحة.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

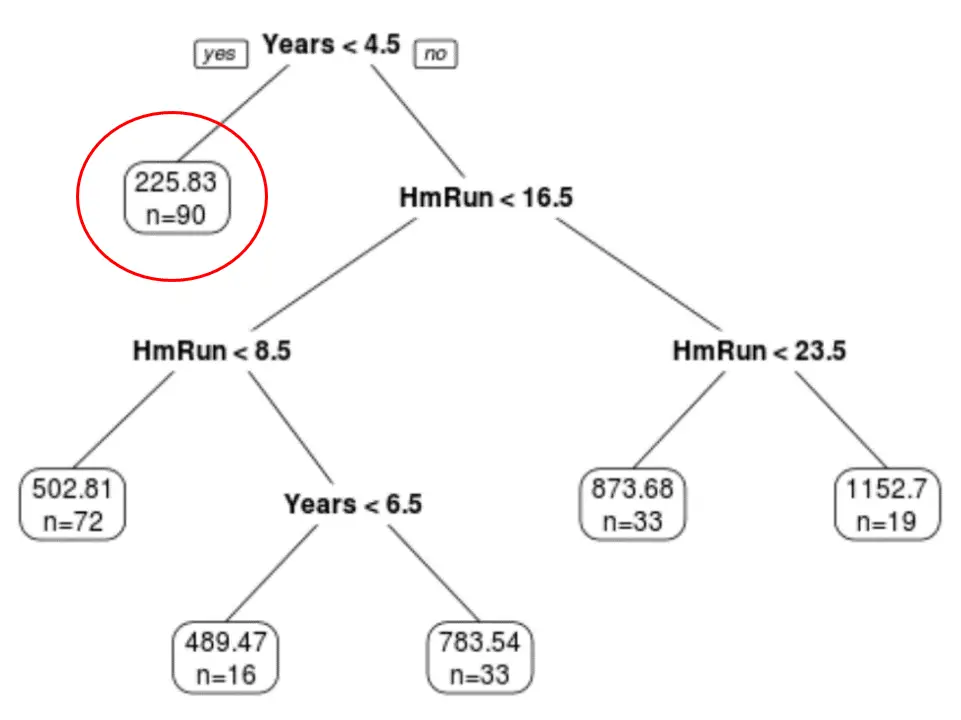
يمكننا أن نرى أن الشجرة المشذبة النهائية بها ست عقد طرفية. تعرض كل عقدة طرفية الراتب المتوقع للاعبين في تلك العقدة بالإضافة إلى عدد الملاحظات من مجموعة البيانات الأصلية التي تنتمي إلى تلك الدرجة.

على سبيل المثال، يمكننا أن نرى أنه في مجموعة البيانات الأصلية، كان هناك 90 لاعبًا لديهم أقل من 4.5 سنوات من الخبرة وكان متوسط رواتبهم 225.83 ألف دولار.

الخطوة 4: استخدم الشجرة لعمل تنبؤات.

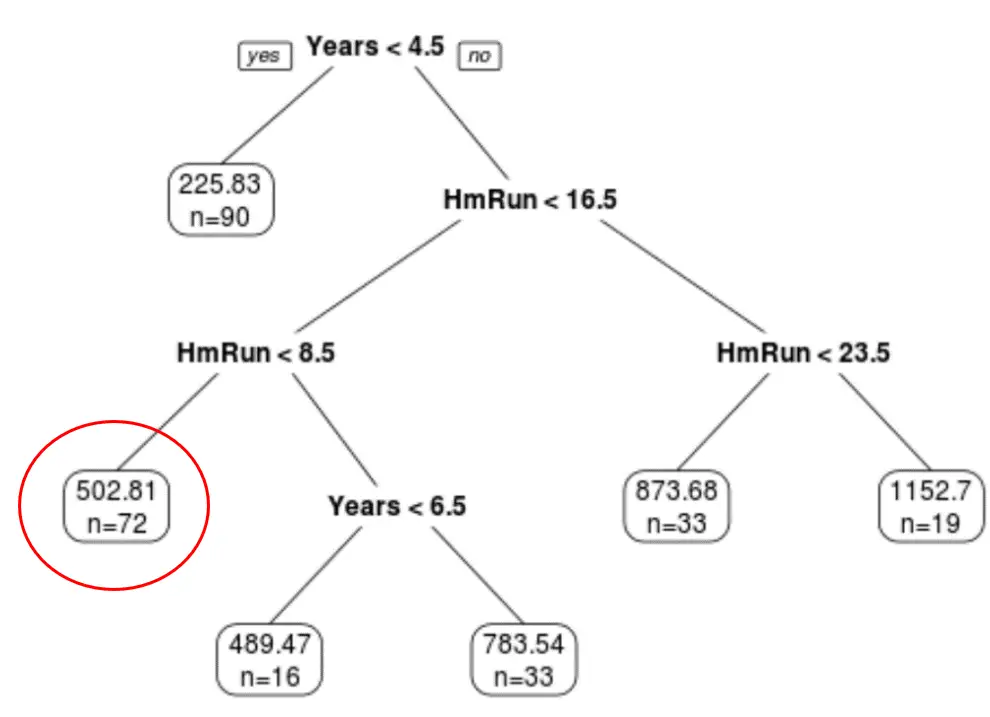
يمكننا استخدام الشجرة المشذبة النهائية للتنبؤ براتب لاعب معين بناءً على سنوات خبرته ومتوسط جولاته على أرضه.

على سبيل المثال، اللاعب الذي لديه 7 سنوات من الخبرة و4 جولات منزلية في المتوسط لديه راتب متوقع قدره 502.81 ألف دولار .

يمكننا استخدام الدالة التنبؤ () في R لتأكيد ذلك:

 #define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079

مثال 2: بناء شجرة تصنيف في R

في هذا المثال، سوف نستخدم مجموعة بيانات ptitanic من الحزمة rpart.plot ، والتي تحتوي على معلومات متنوعة حول الركاب على متن Titanic.

سنستخدم مجموعة البيانات هذه لإنشاء شجرة تصنيف تستخدم متغيرات التوقع مثل الفئة والجنس والعمر للتنبؤ بما إذا كان راكب معين قد نجا أم لا.

استخدم الخطوات التالية لإنشاء شجرة التصنيف هذه.

الخطوة 1: تحميل الحزم اللازمة.

أولاً، سنقوم بتحميل الحزم اللازمة لهذا المثال:

 library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

الخطوة 2: بناء شجرة التصنيف الأولية.

أولاً، سنقوم ببناء شجرة تصنيف أولية كبيرة. يمكننا أن نضمن أن الشجرة كبيرة باستخدام قيمة صغيرة لـ cp ، والتي تشير إلى “معلمة التعقيد”.

وهذا يعني أننا سنقوم بإجراء المزيد من الانقسامات على شجرة التصنيف طالما أن الملاءمة الإجمالية للنموذج تزداد بمقدار القيمة المحددة بواسطة cp على الأقل.

سنستخدم بعد ذلك الدالة printcp() ‎ لطباعة نتائج النموذج:

 #build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age pclass sex   

Root node error: 500/1309 = 0.38197

n=1309 

      CP nsplit rel error xerror xstd
1 0.4240 0 1.000 1.000 0.035158
2 0.0140 1 0.576 0.576 0.029976
3 0.0095 3 0.548 0.578 0.030013
4 0.0070 7 0.510 0.552 0.029517
5 0.0050 9 0.496 0.528 0.029035
6 0.0025 11 0.486 0.532 0.029117
7 0.0020 19 0.464 0.536 0.029198
8 0.0001 22 0.458 0.528 0.029035

الخطوة 3: تقليم الشجرة

بعد ذلك، سنقوم بتقليم شجرة الانحدار للعثور على القيمة المثلى لاستخدامها في cp (معلمة التعقيد) التي تؤدي إلى أقل خطأ في الاختبار.

لاحظ أن القيمة المثلى لـ cp هي القيمة التي تؤدي إلى أدنى خطأ x في الإخراج السابق، والذي يمثل الخطأ في الملاحظات من بيانات التحقق من الصحة.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

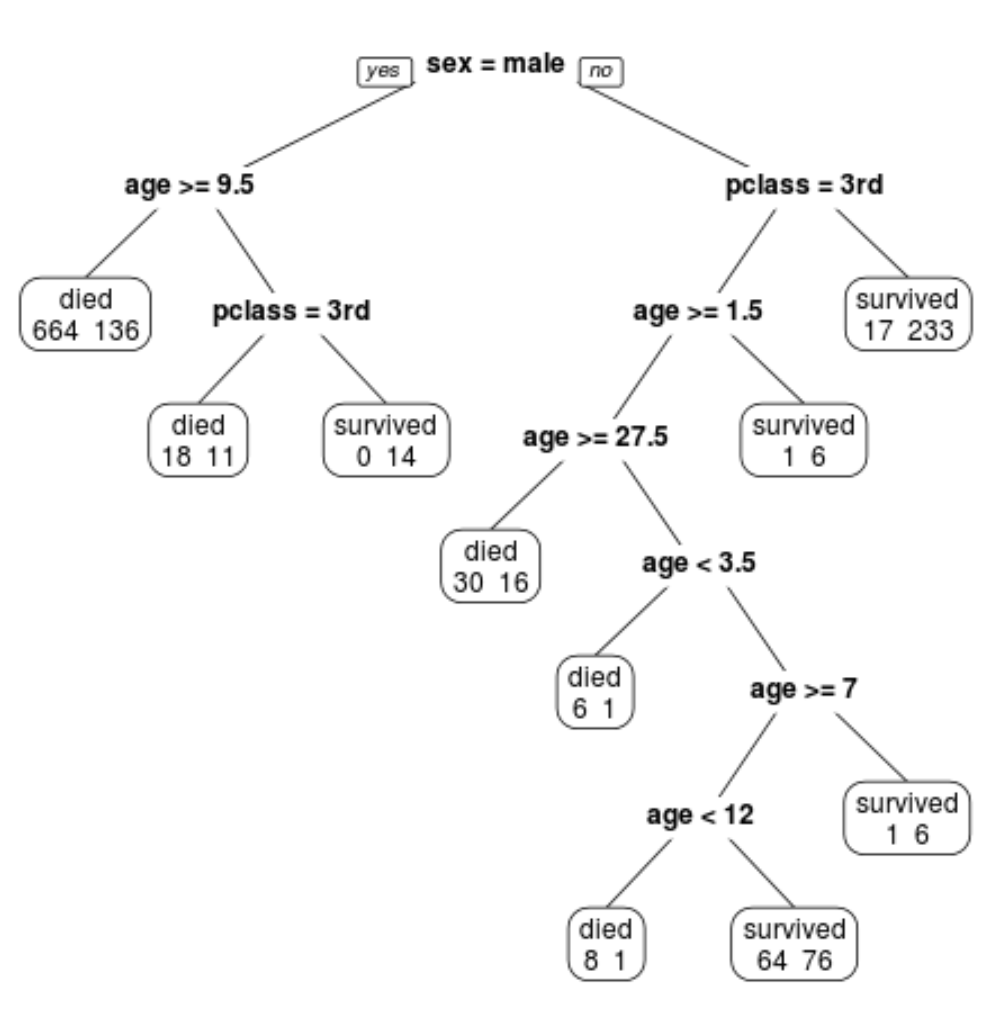
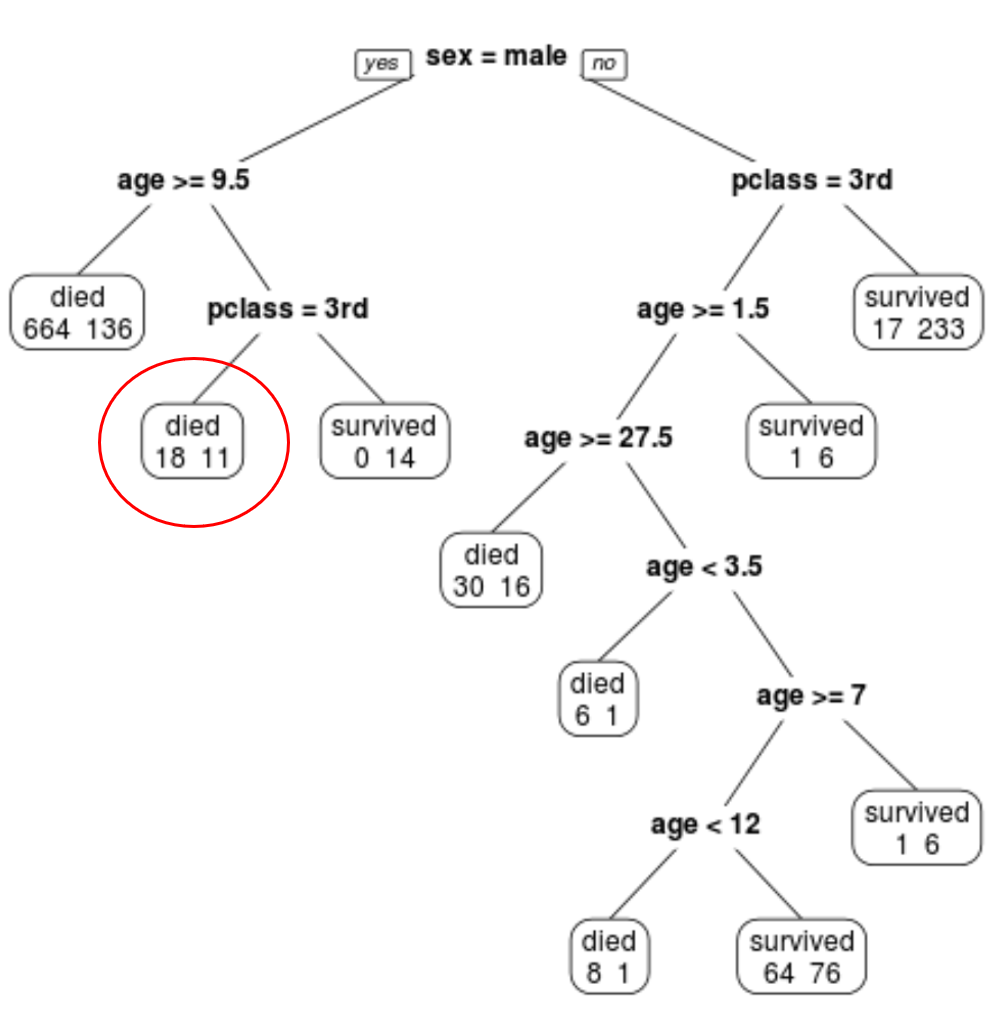
يمكننا أن نرى أن الشجرة المشذبة النهائية تحتوي على 10 عقد طرفية. تشير كل عقدة طرفية إلى عدد الركاب الذين لقوا حتفهم وكذلك عدد الناجين.

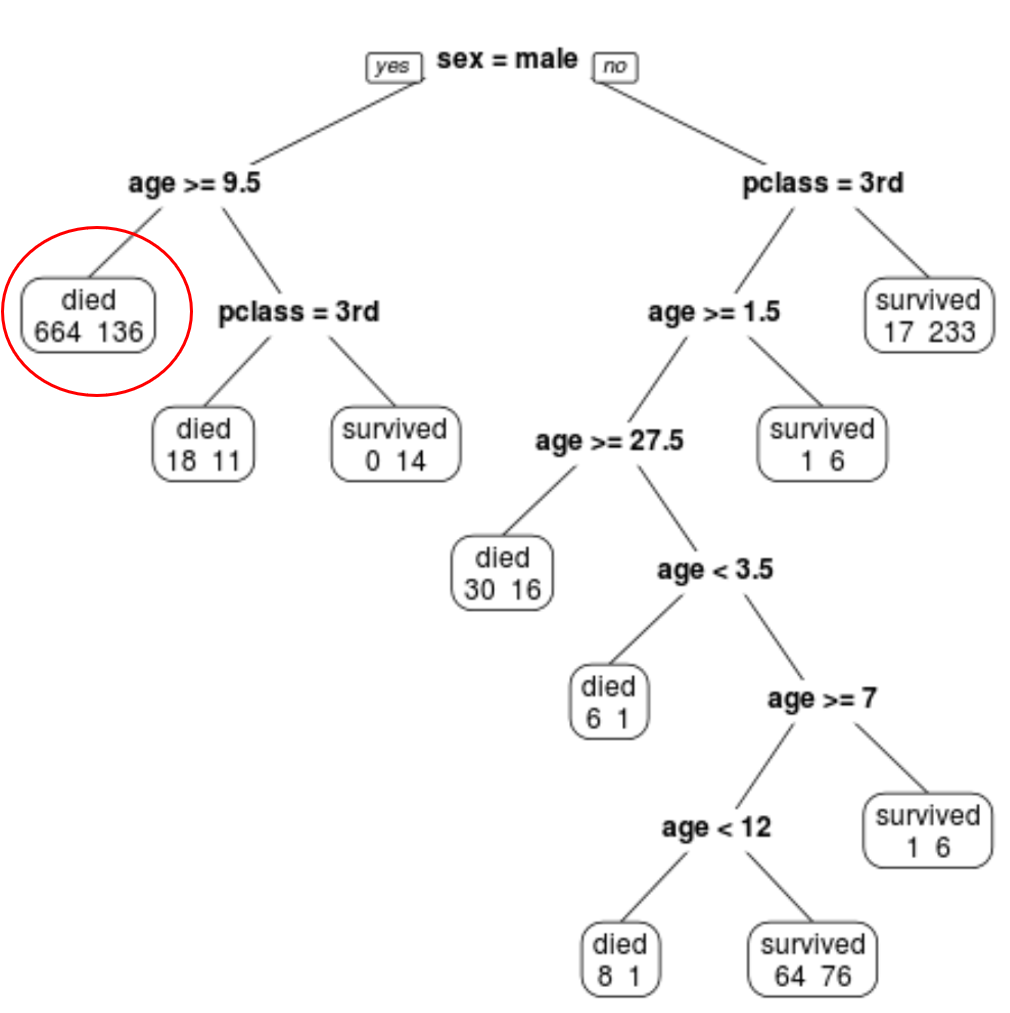
على سبيل المثال، في العقدة الموجودة في أقصى اليسار نرى أن 664 راكبًا لقوا حتفهم ونجا 136.

الخطوة 4: استخدم الشجرة لعمل تنبؤات.

يمكننا استخدام الشجرة المشذبة النهائية للتنبؤ باحتمالية بقاء راكب معين على قيد الحياة بناءً على فئته وعمره وجنسه.

على سبيل المثال، راكب ذكر عمره 8 سنوات وفي الدرجة الأولى لديه احتمال البقاء على قيد الحياة 11/29 = 37.9%.

يمكنك العثور على رمز R الكامل المستخدم في هذه الأمثلة هنا .