الفرق الأقل أهمية فيشر: التعريف + المثال
يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.
الافتراضات المستخدمة في ANOVA هي كما يلي:
H 0 : المتوسطات متساوية لكل مجموعة.
ح أ : إحدى الطرق على الأقل تختلف عن الطرق الأخرى.
إذا كانت القيمة p لتحليل التباين (ANOVA) أقل من مستوى معين من الأهمية (مثل α = 0.05)، فيمكننا رفض فرضية العدم ونستنتج أن إحدى وسائل المجموعة على الأقل تختلف عن الوسائل الأخرى.
ولكن لكي نعرف بالضبط أي المجموعات تختلف عن بعضها البعض، نحتاج إلى إجراء اختبار لاحق.
الاختبار اللاحق الشائع الاستخدام هو اختبار فيشر للفرق الأقل أهمية .
لإجراء هذا الاختبار، نقوم أولاً بحساب إحصائية الاختبار التالية:
LSD = t 0.025 , DF w * √ MS W (1/n 1 + 1/n 1 )
ذهب:
- t .025 , DFw : القيمة الحرجة t لجدول التوزيع t مع α = .025 و DF w تتوافق مع درجات الحرية داخل مجموعات جدول ANOVA.
- MS W : متوسط المربعات داخل المجموعات في جدول ANOVA.
- n 1 , n 2 : أحجام العينات لكل مجموعة
يمكننا بعد ذلك مقارنة متوسط الفرق بين كل مجموعة بإحصائيات الاختبار هذه. إذا كانت القيمة المطلقة لمتوسط الفرق بين مجموعتين أكبر من إحصائية الاختبار، فيمكننا أن نعلن أن هناك فرق ذو دلالة إحصائية بين متوسطي المجموعة.
يوضح المثال التالي كيفية إجراء اختبار فيشر للفرق الأقل أهمية عمليًا.
مثال: اختبار فيشر للفرق الأقل أهمية
لنفترض أن الأستاذ يريد معرفة ما إذا كانت ثلاث تقنيات دراسة مختلفة تؤدي إلى درجات اختبار مختلفة بين الطلاب أم لا. ولاختبار ذلك، قامت بتعيين 10 طلاب بشكل عشوائي لاستخدام كل أسلوب من أساليب الدراسة وتسجيل نتائج امتحاناتهم.
ويبين الجدول التالي نتائج امتحانات كل طالب بناءً على أسلوب الدراسة المستخدم:

يقوم الأستاذ بإجراء تحليل التباين أحادي الاتجاه ويحصل على النتائج التالية:
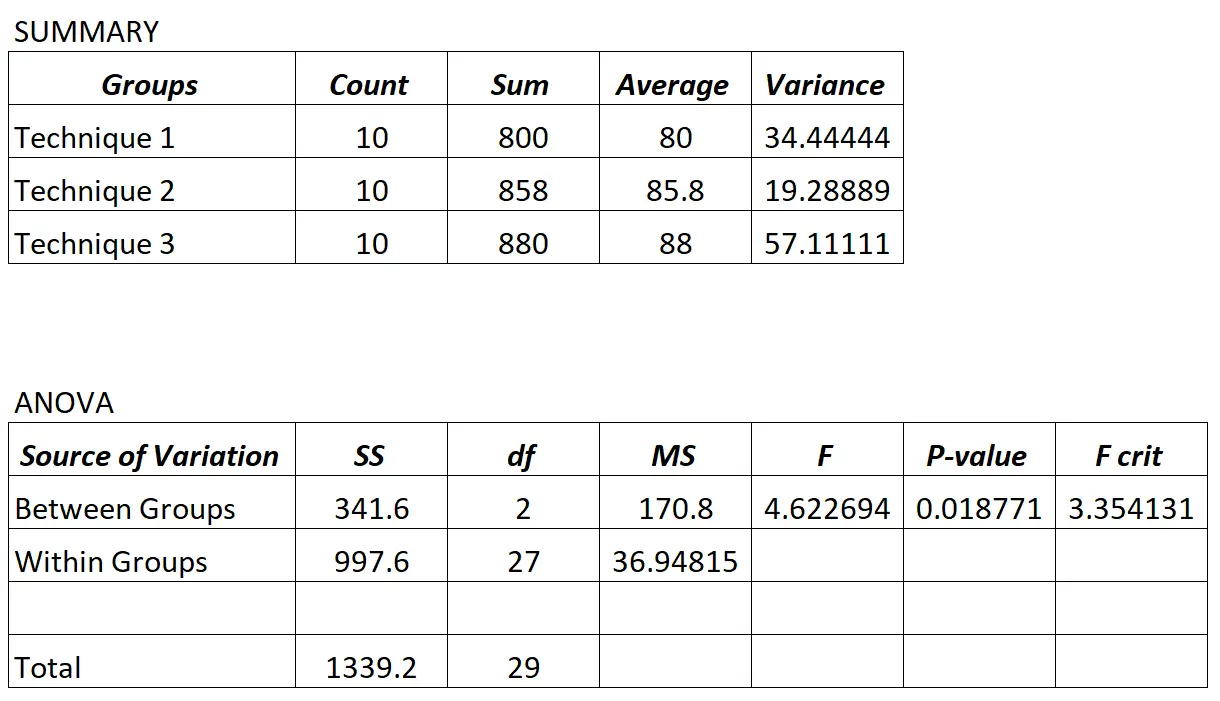
وبما أن القيمة p في جدول ANOVA (0.018771) أقل من 0.05، يمكننا أن نستنتج أن متوسط درجات الامتحانات بين المجموعات الثلاث ليست متساوية.
لذا، يمكننا إجراء اختبار فيشر للفرق الأقل أهمية لتحديد متوسطات المجموعة المختلفة.
باستخدام القيم من نتيجة ANOVA يمكننا حساب إحصائية اختبار فيشر كما يلي:
- LSD = t 0.025 , DFw * √ MS W (1/n 1 + 1/n 1 )
- LSD = ر 0.025 , 27 * √ 36.948*(1/10 + 1/10)
- إل إس دي = 2.052 * √ 7.3896
- إل إس دي = 5.578
يمكننا بعد ذلك حساب متوسط الفرق المطلق بين كل مجموعة:
- التقنية 1 مقابل التقنية 2: |80 – 85.8| = 5.8
- التقنية 1 مقابل التقنية 3: |80 – 88| = 8
- التقنية 2 مقابل التقنية 3: |85.8 – 88| = 2.2
إن فروق المتوسط المطلق بين التقنية 1 والتقنية 2 وبين التقنية 1 والتقنية 3 أكبر من إحصائيات اختبار فيشر. وبالتالي يمكننا أن نستنتج أن هذه التقنيات تؤدي إلى متوسط درجات امتحانات مختلفة بشكل ملحوظ إحصائيًا.
يمكننا أيضًا أن نستنتج أنه لا يوجد فرق كبير في متوسط درجات الاختبار بين التقنية 2 والتقنية 3.