تحليل التباين ثلاثي الاتجاه: التعريف والمثال

يتم استخدام ANOVA ثلاثي الاتجاهات لتحديد كيفية تأثير ثلاثة عوامل مختلفة على متغير الاستجابة.

تعد تحليلات التباين الثلاثية أقل شيوعًا من تحليل التباين أحادي الاتجاه (مع عامل واحد فقط) أو تحليل التباين ثنائي الاتجاه (مع عاملين فقط)، ولكنها لا تزال تستخدم في مجموعة متنوعة من المجالات.

عندما نقوم بإجراء تحليل التباين ثلاثي الاتجاهات، نريد معرفة ما إذا كانت هناك علاقة ذات دلالة إحصائية بين كل عامل ومتغير الاستجابة، وكذلك ما إذا كان هناك أي تأثيرات تفاعل بين العوامل.

يعرض هذا البرنامج التعليمي العديد من السيناريوهات التي يمكنك من خلالها استخدام تحليل التباين ثلاثي الاتجاهات، بالإضافة إلى مثال لكيفية إجراء واحد.

متى يتم استخدام تحليل التباين الثلاثي

فيما يلي بعض السيناريوهات التي يمكنك من خلالها استخدام تحليل التباين الثلاثي:

السيناريو 1: علم النبات

قد يرغب عالم النبات في تحديد كيفية تأثير (1) التعرض للشمس، (2) تكرار الري، و(3) نوع الأسمدة على نمو النبات.

في هذا السيناريو، يمكنها إجراء تحليل التباين ثلاثي الاتجاهات نظرًا لوجود ثلاثة عوامل ومتغير استجابة واحد.

السيناريو 2: البيع بالتجزئة

قد يرغب مدير متجر بيع بالتجزئة في تحديد كيفية تأثير (1) يوم من أيام الأسبوع، و(2) موقع المتجر، و(3) الحملات الإعلانية على إجمالي المبيعات.

في هذا السيناريو، يمكنه إجراء تحليل التباين ثلاثي الاتجاهات نظرًا لوجود ثلاثة عوامل ومتغير استجابة واحد.

السيناريو 3: طبي

قد يرغب الطبيب في تحديد كيفية تأثير (1) الجنس و(2) النظام الغذائي و(3) عادات ممارسة الرياضة على الوزن.

في هذا السيناريو، يمكنها إجراء تحليل التباين ثلاثي الاتجاهات نظرًا لوجود ثلاثة عوامل ومتغير استجابة واحد.

تحليل التباين الثلاثي: مثال

لنفترض أن أحد الباحثين يريد تحديد ما إذا كان برنامج التدريب والجنس وتقسيم الرياضة يؤثر على ارتفاع القفزة.

ولاختبار ذلك، يمكنه إجراء تحليل التباين ثلاثي الاتجاهات باستخدام العوامل التالية:

• 1. البرنامج التدريبي (البرنامج 1 مقابل البرنامج 2)
• 2. الجنس (ذكر أو أنثى)
• 3. القسم الرياضي (القسم الأول مقابل القسم الثاني)

سيكون متغير الاستجابة الوحيد هو ارتفاع القفزة .

لنفترض أنه قام بجمع هذه البيانات عن 40 شخصًا:

ثم يستخدم برنامجًا إحصائيًا لإجراء تحليل التباين ثلاثي الاتجاهات ويحصل على النتيجة التالية:

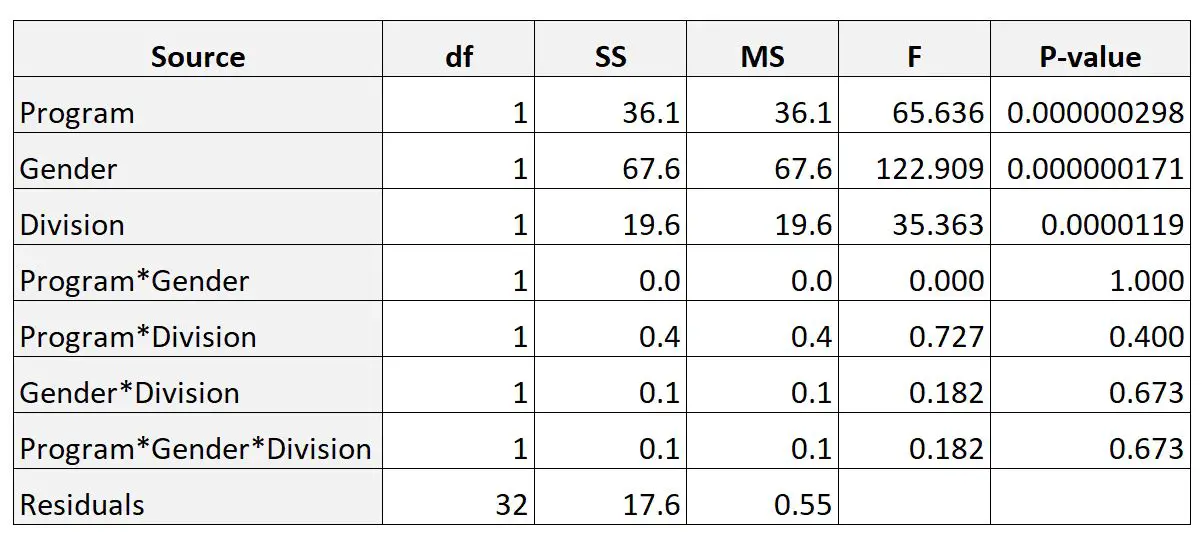
يعرض عمود القيمة P القيمة P لكل عامل على حدة والتفاعلات بين العوامل.

ومن النتائج يمكننا أن نرى أن أيا من التفاعلات بين العوامل الثلاثة لم تكن ذات دلالة إحصائية.

يمكننا أيضًا أن نرى أن كل عامل من العوامل الثلاثة (البرنامج والجنس والقسم) كان ذا دلالة إحصائية.

في الختام، يمكننا القول أن البرنامج التدريبي والجنس والتقسيم كلها مؤشرات هامة لزيادة ارتفاع القفز لدى اللاعبين.

ونود أن نقول أيضًا أنه لا توجد تأثيرات تفاعلية كبيرة بين هذه العوامل الثلاثة.

ملحوظة : من الناحية العملية، نقوم أيضًا بحساب متوسط ارتفاع القفزة لكل برنامج وجنس وقسم حتى نتمكن من تحديد مستويات كل عامل المرتبطة بزيادة ارتفاع القفزة.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء ANOVA ثلاثي الاتجاهات في R وPython:

كيفية إجراء ANOVA ثلاثي الاتجاهات في R
كيفية إجراء ANOVA ثلاثي الاتجاهات في بايثون