كيفية إجراء تحليل التباين ثنائي الاتجاه يدويًا

يتم استخدام ANOVA ثنائي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر تم تقسيمها على عاملين أم لا.

يشرح هذا البرنامج التعليمي كيفية إجراء ANOVA ثنائي الاتجاه يدويًا.

مثال: تحليل التباين اليدوي ثنائي الاتجاه

لنفترض أن عالم النبات يريد معرفة ما إذا كان نمو النبات يتأثر بالتعرض لأشعة الشمس وتكرار الري. تزرع 40 بذرة وتتركها تنمو لمدة شهر في ظروف مختلفة من التعرض لأشعة الشمس وتكرار الري.

وبعد شهر، تسجل ارتفاع كل نبات. النتائج موضحة أدناه:

في الجدول أعلاه نرى أنه تم زراعة خمسة نباتات في كل مجموعة من الظروف.

على سبيل المثال، تمت زراعة خمسة نباتات بسقي يومي وبدون ضوء الشمس وكان ارتفاعها بعد شهرين 4.8 بوصة، 4.4 بوصة، 3.2 بوصة، 3.9 بوصة، 4.4 بوصة:

يمكننا استخدام الخطوات التالية لإجراء تحليل التباين ثنائي الاتجاه:

الخطوة 1: حساب مجموع المربعات للعامل الأول (تكرار الري)

أولاً، سنقوم بحساب متوسط الارتفاع الإجمالي للنباتات الأربعين:

المتوسط العام = (4.8 + 5 + 6.4 + 6.3 + … + 3.9 + 4.8 + 5.5 + 5.5) / 40 = 5.1525

بعد ذلك، سوف نقوم بحساب متوسط ارتفاع جميع النباتات التي يتم سقيها يوميًا:

المتوسط اليومي = (4.8 + 5 + 6.4 + 6.3 + … + 4.4 + 4.8 + 5.8 + 5.8) /20 = 5.155

بعد ذلك، سوف نقوم بحساب متوسط ارتفاع جميع النباتات التي يتم سقيها كل أسبوع:

المتوسط الأسبوعي = (4.4 + 4.9 + 5.8 + 6 + … + 3.9 + 4.8 + 5.5 + 5.5) /20 = 5.15

بعد ذلك، سنقوم بحساب مجموع المربعات لعامل “تكرار الري” باستخدام الصيغة التالية:

Σن(X _ي – X ..) ²

ذهب:

• n : حجم العينة للمجموعة j
• Σ : رمز يوناني معناه “المجموع”
• X _j : متوسط المجموعة j
• عاشراً .. : المتوسط الكبير

في مثالنا، نحسب مجموع المربعات لعامل “تكرار الري” على النحو التالي: 20(5.155-5.1525) ² + 20(5.15-5.1525) ² = 0.00025

الخطوة الثانية: حساب مجموع المربعات للعامل الثاني (التعرض للشمس)

أولاً، سنقوم بحساب متوسط الارتفاع الإجمالي للنباتات الأربعين:

المتوسط العام = (4.8 + 5 + 6.4 + 6.3 + … + 3.9 + 4.8 + 5.5 + 5.5) / 40 = 5.1525

وبعد ذلك سوف نقوم بحساب متوسط ارتفاع جميع النباتات التي لم تتعرض للشمس:

المتوسط بدون الشمس = (4.8 + 4.4 + 3.2 + 3.9 + 4.4 + 4.4 + 4.2 + 3.8 + 3.7 + 3.9) / 10 = 4.07

سنكرر هذه العملية الحسابية لإيجاد متوسط ارتفاع النباتات المعرضة لمختلف أنواع التعرض لأشعة الشمس:

• متوسط سطوع الشمس المنخفض = 5.1
• متوسط متوسط ضوء الشمس = 5.89
• متوسط سطوع الشمس العالي = 5.55

بعد ذلك، سوف نقوم بحساب مجموع المربعات لعامل “التعرض للشمس” باستخدام الصيغة التالية:

Σن(X _ي – X ..) ²

ذهب:

• n : حجم العينة للمجموعة j
• Σ : رمز يوناني معناه “المجموع”
• X _j : متوسط المجموعة j
• عاشراً .. : المتوسط الكبير

في مثالنا، نحسب مجموع المربعات لعامل “التعرض للشمس” كما يلي: 10(4.07-5.1525) ² + 10(5.1-5.1525) ² + 10(5.89 -5.1525) ² + 10(5.55-5.1525) ² = 18.76475

الخطوة 3: حساب مجموع المربعات بالداخل (خطأ)

بعد ذلك، سنقوم بحساب مجموع المربعات عن طريق أخذ مجموع مربعات الاختلافات بين كل مجموعة من العوامل وارتفاعات النباتات الفردية.

على سبيل المثال، متوسط ارتفاع جميع النباتات التي تسقى يوميا دون التعرض لأشعة الشمس هو 4.14. يمكننا بعد ذلك حساب مجموع مربعات الاختلافات لكل من هذه النباتات الفردية على النحو التالي:

• SS للسقي اليومي وبدون شمس: (4.8-4.14) ² + (4.4-4.14) ² + (3.2-4.14) ² + (3.9-4.14) ² + (4.4-4.14) ² = 1.512

يمكننا تكرار هذه العملية لكل مجموعة من العوامل:

• SS للسقي اليومي وأشعة الشمس المنخفضة: 0.928
• SS للسقي اليومي ومتوسط ضوء الشمس: 1,788
• SS للسقي اليومي وأشعة الشمس القوية: 1.648
• SS للسقي الأسبوعي بدون شمس: 0.34
• SS للري الأسبوعي وأشعة الشمس المنخفضة: 0.548
• SS للسقي الأسبوعي ومتوسط أشعة الشمس: 0.652
• SS للري الأسبوعي وأشعة الشمس القوية: 1,268

يمكننا بعد ذلك أخذ مجموع كل هذه القيم للعثور على مجموع المربعات الموجودة داخل (خطأ):

مجموع المربعات داخل = 1.512 + 0.928 + 1.788 + 1.648 + 0.34 + 0.548 + 0.652 + 1.268 = 8.684

الخطوة 4: حساب مجموع المربعات

ثم يمكننا حساب المجموع الإجمالي للمربعات عن طريق أخذ مجموع الفروق بين ارتفاع كل نبات والمتوسط الكلي:

مجموع المربعات = (4.8 – 5.1525) ² + (5 – 5.1525) ² + … + (5.5 – 5.1525) ² = 28.45975

الخطوة 5: حساب مجموع تفاعل المربعات

بعد ذلك، سوف نقوم بحساب مجموع تفاعل المربعات باستخدام الصيغة التالية:

• التفاعل SS = إجمالي SS – عامل SS 1 – عامل SS 2 – SS الداخلي
• تفاعل SS = 28.45975 – 0.00025 – 18.76475 – 8.684
• تفاعل SS = 1.01075

الخطوة 6: أكمل جدول تحليل التباين (ANOVA).

وأخيرا، سوف نقوم بملء القيم من جدول ANOVA ثنائي الاتجاه:

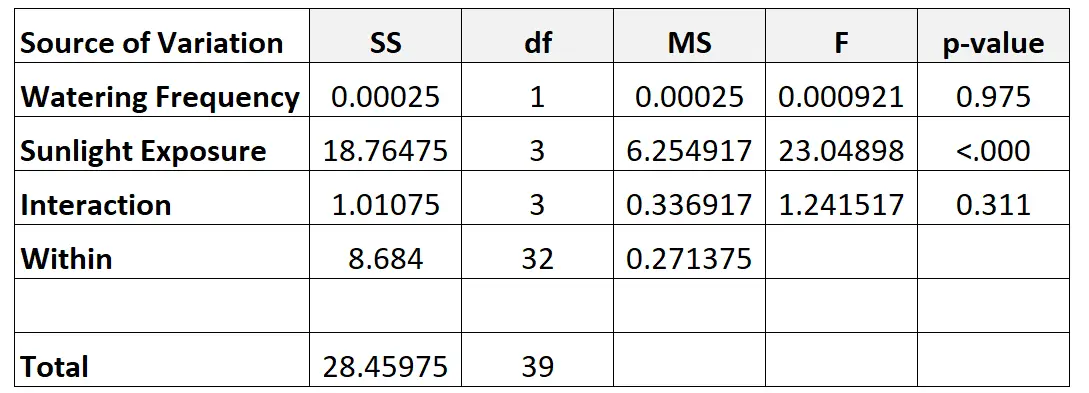
وإليك كيفية حساب الأرقام المختلفة في الجدول:

• df تردد الري: d-1 = 2-1 = 1
• التعرض لأشعة الشمس: k-1 = 4-1 = 3
• التفاعل df : (j-1)*(k-1) = 1*3 = 3
• df In : n – (j*k) = 40 – (2*4) = 32
• إجمالي df: n-1 = 40-1 = 39
• مرض التصلب العصبي المتعدد: سس / مدافع
• تردد الري F : تردد الري MS/MS الداخلي
• F التعرض لأشعة الشمس : التعرض لأشعة الشمس MS / MS داخل المنزل
• التفاعل F : التفاعل MS / MS داخل
• تردد الري ذو القيمة p : القيمة p التي تتوافق مع القيمة F البالغة 0.000921 مع البسط df = 1 والمقام df = 32
• القيمة p للتعرض للشمس : القيمة p التي تتوافق مع القيمة F البالغة 23.04898 مع البسط df = 3 والمقام df = 32
• تفاعل القيمة p : القيمة p التي تقابل القيمة F البالغة 1.241517 مع البسط df = 3 والمقام df = 32

ملاحظة رقم 1: n = إجمالي عدد الملاحظات، j = عدد مستويات تكرار الري، k = عدد مستويات التعرض لأشعة الشمس.

ملاحظة رقم 2 : تم حساب القيم p التي تتوافق مع القيمة F باستخدام حاسبة التوزيع F.

الخطوة 7: تفسير النتائج

يمكننا ملاحظة ما يلي من جدول ANOVA:

• وكانت القيمة p للتفاعل بين تكرار الري والتعرض للشمس 0.311 . هذا ليس ذو دلالة إحصائية عند α = 0.05.
• وكانت القيمة p لتكرار الري 0.975 . هذا ليس ذو دلالة إحصائية عند α = 0.05.
• كانت القيمة p للتعرض لأشعة الشمس <0.000 . وهذا ذو دلالة إحصائية عند α = 0.05.

تشير هذه النتائج إلى أن التعرض لأشعة الشمس هو العامل الوحيد الذي له تأثير ذو دلالة إحصائية على ارتفاع النبات.

وبما أنه لا يوجد أي تأثير تفاعلي، فإن تأثير التعرض لأشعة الشمس يكون ثابتًا عند كل مستوى من مستويات تكرار الري.

ببساطة، ما إذا كان يتم ري النبات يوميًا أو أسبوعيًا ليس له أي تأثير على كيفية تأثير التعرض لأشعة الشمس على النبات.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول ANOVAs:

كيفية إجراء ANOVA أحادي الاتجاه يدويًا
كيفية إجراء ANOVA للتدابير المتكررة يدويًا
الدليل الكامل: كيفية الإبلاغ عن نتائج ANOVA ثنائية الاتجاه