كيفية إجراء تحليل التباين (anova) بأحجام عينات غير متساوية

السؤال الذي يطرحه الطلاب غالبًا عندما يتعلق الأمر بالإحصاءات هو:

هل من الممكن إجراء تحليل التباين الأحادي (ANOVA) عندما تكون أحجام العينات لكل مجموعة غير متساوية؟

الجواب القصير:

نعم، يمكنك إجراء تحليل التباين أحادي الاتجاه عندما لا تكون أحجام العينات متساوية. لا تعد أحجام العينات المتساوية أحد الافتراضات الواردة في تحليل التباين (ANOVA).

ومع ذلك، هناك مشكلتان محتملتان يجب أخذهما في الاعتبار عند إجراء تحليل التباين (ANOVA) أحادي الاتجاه بأحجام عينات غير متساوية:

(1) انخفاض القوة الإحصائية.

(2) تم تقليل المتانة إلى التباين غير المتكافئ.

تشرح الأقسام التالية هاتين المشكلتين المحتملتين بالتفصيل.

المشكلة رقم 1: انخفاض القوة الإحصائية

عندما نستخدم أي نوع من الاختبارات الإحصائية لمقارنة المجموعات، تكون القوة الإحصائية للاختبار أعلى عندما يكون لكل مجموعة حجم عينة متساوٍ.

تذكر أن القوة الإحصائية تشير إلى احتمال أن يكتشف الاختبار تأثيرًا ما عندما يكون موجودًا بالفعل.

يمكن إثبات أنه كلما زادت اختلافات حجم العينة بين المجموعات، انخفضت القوة الإحصائية لتحليل التباين (ANOVA).

ولهذا السبب يريد الباحثون عمومًا أحجامًا متساوية للعينات من أجل الحصول على قوة أعلى وبالتالي احتمالية أكبر لاكتشاف الاختلافات الحقيقية.

من الممكن بالتأكيد إجراء تحليل التباين أحادي الاتجاه بأحجام عينات غير متساوية، ولكن يجب أن تدرك أنه سيتم تقليل قوة تحليل التباين أحادي الاتجاه.

المشكلة رقم 2: تم تقليل المتانة إلى التباين غير المتكافئ

أحد افتراضات ANOVA أحادية الاتجاه هو أن التباين بين كل مجموعة متساوي.

بشكل عام، يعتبر تحليل التباين أحادي الاتجاه قويًا لانتهاكات افتراض التباينات المتساوية، ولكن فقط إذا كان لكل مجموعة نفس حجم العينة .

لذا، إذا كان لديك أحجام عينات غير متساوية وتباينات غير متساوية بين المجموعات، فقد يكون من الصعب الوثوق بنتائج ANOVA أحادية الاتجاه.

كيفية تحديد ما إذا كنت تريد استخدام ANOVA أحادي الاتجاه مع أحجام عينات غير متساوية

إذا كانت لديك أحجام عينة غير متساوية وترغب في إجراء تحليل التباين (ANOVA) أحادي الاتجاه لاختبار الاختلافات بين متوسطات المجموعة، فيمكنك استخدام المخطط الانسيابي التالي لتحديد كيفية المتابعة:

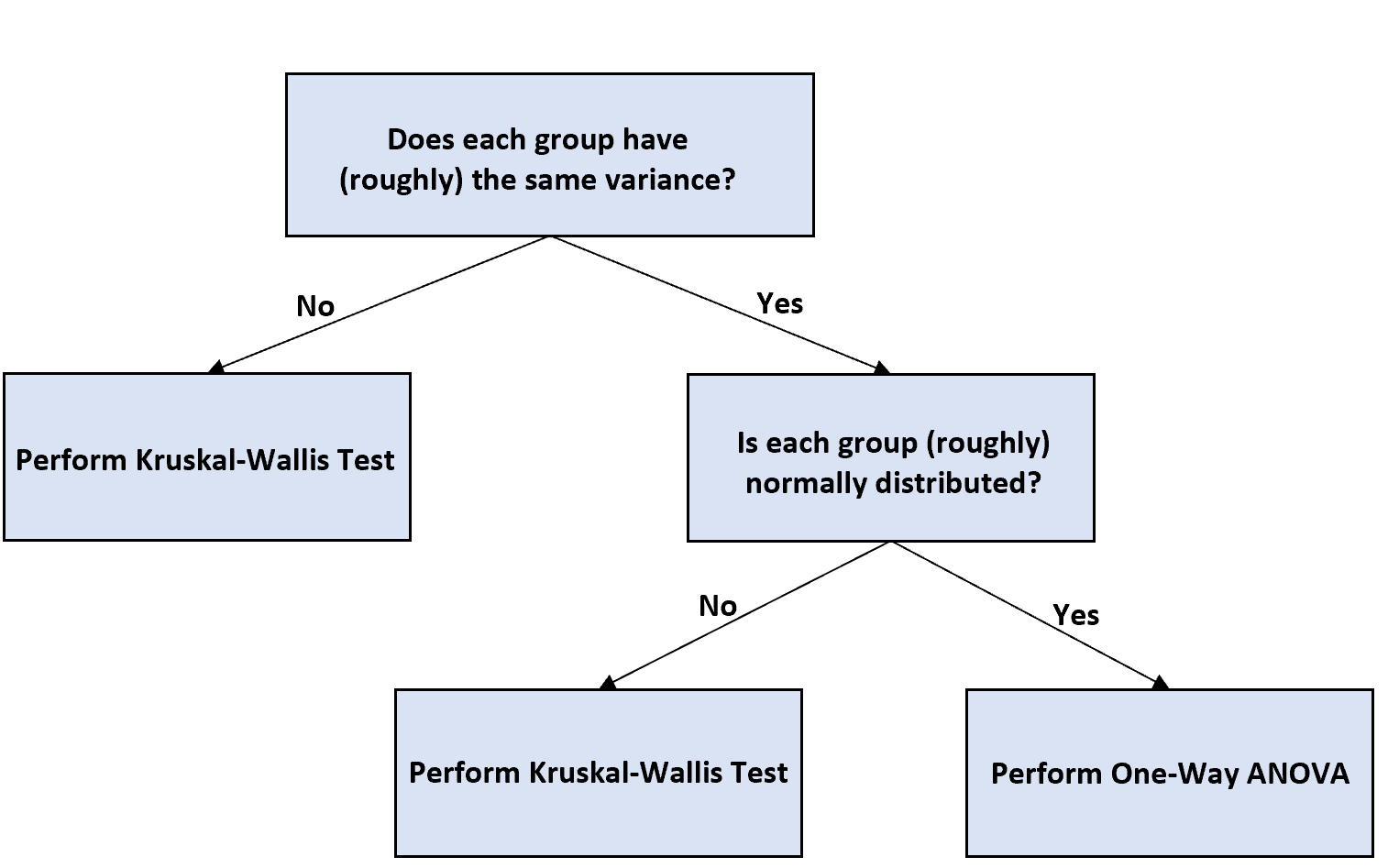
فيما يلي شرح موجز للمخطط الانسيابي:

الخطوة 1: تحديد ما إذا كانت كل مجموعة لها نفس التباين.

لتحديد ما إذا كانت كل مجموعة لها نفس التباين، يمكنك استخدام إحدى الطريقتين التاليتين:

• قم بإنشاء boxplots لكل مجموعة ومعرفة ما إذا كان توزيع القيم في كل مجموعة متساويًا تقريبًا.
• إجراء اختبار إحصائي رسمي للتباينات المتساوية مثل اختبار بارتليت .

إذا كانت التباينات غير متساوية، قم بإجراء اختبار كروسكال واليس ، والذي يعتبر المعادل اللامعلمي لتحليل التباين أحادي الاتجاه.

إذا كانت الفجوات متساوية، انتقل إلى الخطوة التالية.

الخطوة 2: تحديد ما إذا كانت كل مجموعة موزعة بشكل طبيعي.

لتحديد ما إذا كانت القيم في كل مجموعة موزعة بشكل طبيعي تقريبًا، يمكنك استخدام أحد الطريقتين:

• قم بإنشاء رسوم بيانية أو مخططات QQ لكل مجموعة.
• قم بإجراء اختبارات إحصائية رسمية مثل Shapiro-Wilk، أو Kolmogorov-Smironov، أو Jarque-Barre، أو D’Agostino-Pearson.

إذا تم توزيع كل مجموعة بشكل طبيعي، فيمكنك إجراء تحليل التباين أحادي الاتجاه وتفسير النتائج كما تفعل مع أي تحليل التباين العادي أحادي الاتجاه.

إذا لم يتم توزيع كل مجموعة بشكل طبيعي، قم بإجراء اختبار كروسكال واليس بدلاً من ذلك.

مصادر إضافية

مقدمة إلى تحليل التباين الأحادي (One-Way ANOVA).
كيفية التحقق من افتراضات ANOVA
مقدمة لاختبار كروسكال واليس
كيفية تفسير قيمة F وقيمة P في ANOVA