تحليل التباين ثنائي الاتجاه: التعريف والصيغة والمثال

يتم استخدام ANOVA ثنائي الاتجاه (“تحليل التباين”) لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر تم تخصيصها لمتغيرين (تسمى أحيانًا “العوامل”).

يشرح هذا البرنامج التعليمي ما يلي:

• متى يتم استخدام تحليل التباين ثنائي الاتجاه.
• الافتراضات التي يجب الوفاء بها لإجراء تحليل التباين ثنائي الاتجاه.
• مثال على كيفية إجراء تحليل التباين ثنائي الاتجاه.

متى يتم استخدام تحليل التباين ثنائي الاتجاه

يجب عليك استخدام تحليل التباين ثنائي الاتجاه عندما تريد معرفة كيفية تأثير عاملين على متغير الاستجابة وما إذا كان هناك تأثير تفاعل بين العاملين على متغير الاستجابة أم لا.

على سبيل المثال، لنفترض أن عالم النبات يريد استكشاف كيفية تأثير التعرض لأشعة الشمس وتكرار الري على نمو النبات. تزرع 40 بذرة وتتركها تنمو لمدة شهرين في ظروف مختلفة من التعرض لأشعة الشمس وتكرار الري. وبعد شهرين، تسجل ارتفاع كل نبات.

في هذه الحالة لدينا المتغيرات التالية:

• متغير الاستجابة: نمو النبات
• العوامل: التعرض لأشعة الشمس، وتكرار الري

و نود الإجابة على الأسئلة التالية:

• هل يؤثر التعرض لأشعة الشمس على نمو النبات؟
• هل يؤثر تكرار الري على نمو النبات؟
• هل هناك تأثير تفاعلي بين التعرض لأشعة الشمس وتكرار الري؟ (على سبيل المثال، تأثير التعرض لأشعة الشمس على النباتات يعتمد على تكرار الري)

سوف نستخدم ANOVA ثنائي الاتجاه لهذا التحليل لأن لدينا عاملين . إذا أردنا، بدلاً من ذلك، معرفة مقدار تأثير تكرار الري على نمو النبات، فسنستخدم تحليل التباين أحادي الاتجاه لأننا سنعمل مع عامل واحد فقط.

افتراضات ANOVA في اتجاهين

لكي تكون نتائج تحليل التباين ثنائي الاتجاه صحيحة، يجب استيفاء الافتراضات التالية:

1. الحالة الطبيعية – يتم توزيع متغير الاستجابة بشكل طبيعي تقريبًا لكل مجموعة.

2. الاختلافات المتساوية – يجب أن تكون الفروق لكل مجموعة متساوية تقريبًا.

3. الاستقلال – الملاحظات داخل كل مجموعة مستقلة عن بعضها البعض وتم الحصول على الملاحظات داخل المجموعات عن طريق أخذ عينات عشوائية.

تحليل التباين ثنائي الاتجاه: مثال

يريد عالم النبات معرفة ما إذا كان نمو النبات يتأثر بالتعرض لأشعة الشمس وتكرار الري. تزرع 40 بذرة وتتركها تنمو لمدة شهرين في ظروف مختلفة من التعرض لأشعة الشمس وتكرار الري. وبعد شهرين، تسجل ارتفاع كل نبات. النتائج موضحة أدناه:

في الجدول أعلاه نرى أنه تم زراعة خمسة نباتات في كل مجموعة من الظروف.

على سبيل المثال، تمت زراعة خمسة نباتات بسقي يومي وبدون ضوء الشمس وكان ارتفاعها بعد شهرين 4.8 بوصة، 4.4 بوصة، 3.2 بوصة، 3.9 بوصة، 4.4 بوصة:

تقوم بإجراء ANOVA ثنائي الاتجاه في Excel وتحصل على النتيجة التالية:

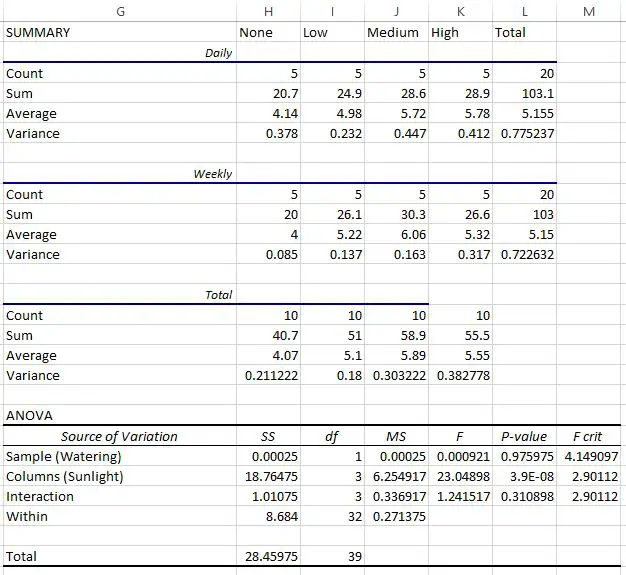
ويبين الجدول الأخير نتيجة تحليل التباين ثنائي الاتجاه. يمكننا أن نلاحظ ما يلي:

• وكانت القيمة p للتفاعل بين تكرار الري والتعرض للشمس 0.310898 . وهذا ليس ذو دلالة إحصائية عند مستوى 0.05 ألفا.
• وكانت القيمة p لتكرار الري 0.975975 . وهذا ليس ذو دلالة إحصائية عند مستوى 0.05 ألفا.
• كانت القيمة p للتعرض لأشعة الشمس 3.9E-8 (0.000000039) . وهذا ذو دلالة إحصائية عند مستوى ألفا 0.05.

تشير هذه النتائج إلى أن التعرض لأشعة الشمس هو العامل الوحيد الذي له تأثير ذو دلالة إحصائية على ارتفاع النبات.

وبما أنه لا يوجد أي تأثير تفاعلي، فإن تأثير التعرض لأشعة الشمس يكون ثابتًا عند كل مستوى من مستويات تكرار الري.

ببساطة، ما إذا كان يتم ري النبات يوميًا أو أسبوعيًا ليس له أي تأثير على كيفية تأثير التعرض لأشعة الشمس على النبات.

مصادر إضافية

تشرح المقالات التالية كيفية إجراء تحليل التباين ثنائي الاتجاه باستخدام برامج إحصائية مختلفة:

كيفية إجراء ANOVA ثنائي الاتجاه في Excel
كيفية إجراء ANOVA ثنائي الاتجاه في R
كيفية إجراء ANOVA ثنائي الاتجاه في بايثون
كيفية إجراء تحليل التباين ثنائي الاتجاه في برنامج SPSS
كيفية إجراء ANOVA ثنائي الاتجاه في Stata