كيفية إجراء تحليل التباين المتداخل (nested anova) في r (خطوة بخطوة)

ANOVA المتداخلة هو نوع من ANOVA (“تحليل التباين”) حيث يتم دمج عامل واحد على الأقل ضمن عامل آخر.

على سبيل المثال، لنفترض أن أحد الباحثين يريد معرفة ما إذا كانت ثلاثة أسمدة مختلفة تنتج مستويات مختلفة من نمو النبات.

لاختبار ذلك، قام ثلاثة فنيين مختلفين برش السماد A على أربع نباتات، وقام ثلاثة فنيين آخرين برش السماد B على أربع نباتات، وقام ثلاثة فنيين آخرين برش السماد C على أربع نباتات.

في هذا السيناريو، متغير الاستجابة هو نمو النبات والعاملين هما الفني والأسمدة. اتضح أن الفني يقع في الأسمدة:

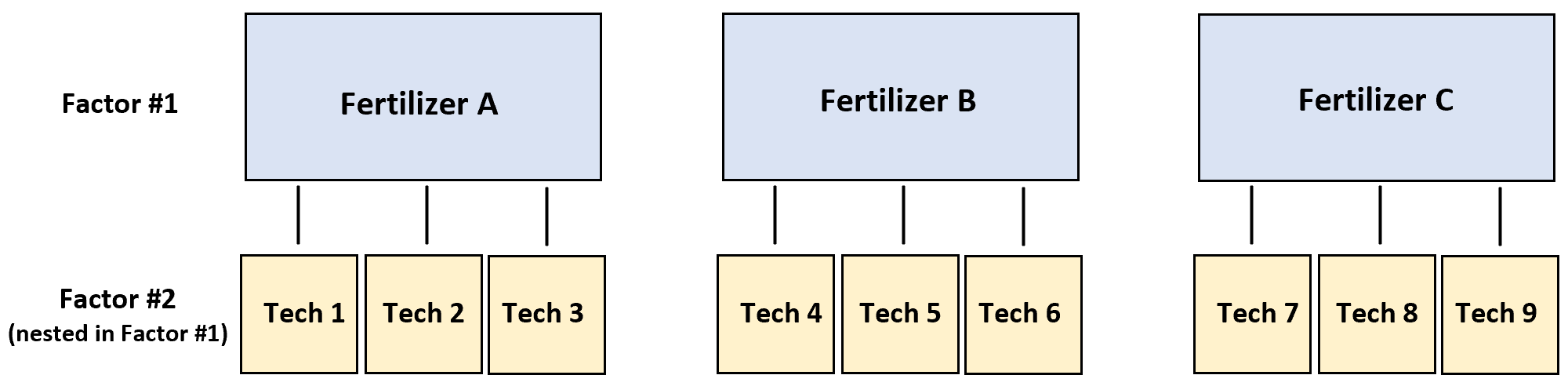
يوضح المثال التالي خطوة بخطوة كيفية إجراء ANOVA المتداخل في R.

الخطوة 1: إنشاء البيانات

أولاً، لنقم بإنشاء إطار بيانات للاحتفاظ ببياناتنا في R:

 #create data
df <- data. frame (growth=c(13, 16, 16, 12, 15, 16, 19, 16, 15, 15, 12, 15,
                          19, 19, 20, 22, 23, 18, 16, 18, 19, 20, 21, 21,
                          21, 23, 24, 22, 25, 20, 20, 22, 24, 22, 25, 26),
                 fertilizer=c(rep(c(' A ', ' B ', ' C '), each= 12 )),
                 tech=c(rep(1:9, each= 4 )))

#view first six rows of data
head(df)

  growth fertilizer tech
1 13 A 1
2 16 A 1
3 16 A 1
4 12 A 1
5 15 A 2
6 16 A 2

الخطوة 2: ضبط ANOVA المتداخلة

يمكننا استخدام بناء الجملة التالي لتناسب ANOVA المتداخلة في R:

aov (الإجابة ~ العامل A / العامل B)

ذهب:

• الاستجابة: متغير الاستجابة
• العامل أ: العامل الأول
• العامل ب: العامل الثاني المتداخل في العامل الأول

يوضح الكود التالي كيفية ملاءمة ANOVA المتداخلة لمجموعة البيانات الخاصة بنا:

 #fit nested ANOVA
nest <- aov(df$growth ~ df$fertilizer / factor(df$tech))

#view summary of nested ANOVA
summary(nest)

                              Df Sum Sq Mean Sq F value Pr(>F)    
df$fertilizer 2 372.7 186.33 53.238 4.27e-10 ***
df$fertilizer:factor(df$tech) 6 31.8 5.31 1.516 0.211    
Residuals 27 94.5 3.50                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

الخطوة 3: تفسير النتيجة

يمكننا أن ننظر إلى عمود القيمة p لتحديد ما إذا كان لكل عامل تأثير ذو دلالة إحصائية على نمو النبات أم لا.

من الجدول أعلاه، يمكننا أن نرى أن الأسمدة لها تأثير ذو دلالة إحصائية على نمو النبات (قيمة p <0.05)، ولكن ليس له تأثير فني (قيمة p = 0.211).

وهذا يخبرنا أننا إذا أردنا زيادة نمو النبات، فإننا بحاجة إلى التركيز على الأسمدة المستخدمة بدلاً من الفني الفردي الذي يقوم بتطبيق الأسمدة.

الخطوة 4: تصور النتائج

أخيرًا، يمكننا استخدام المخططات الصندوقية لتصور توزيع نمو النبات حسب الأسمدة والفني:

 #load ggplot2 data visualization package
library (ggplot2)

#create boxplots to visualize plant growth
ggplot(df, aes (x=factor(tech), y=growth, fill=fertilizer)) +
  geom_boxplot()

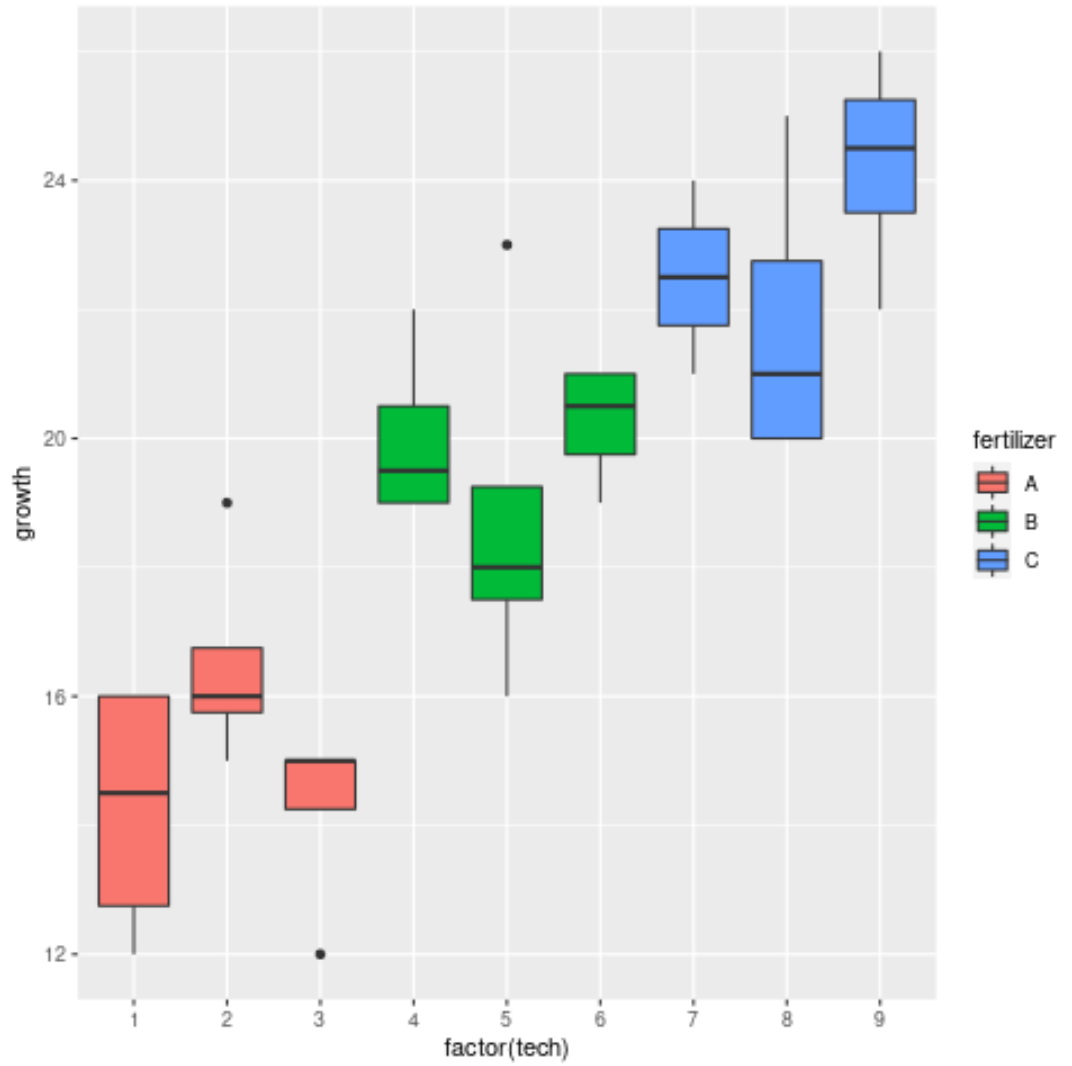
يوضح الرسم البياني أن هناك تباينًا كبيرًا في النمو بين الأسمدة الثلاثة المختلفة، ولكن لا يوجد تباين كبير بين الفنيين داخل كل مجموعة أسمدة.

ويبدو أن هذا يطابق نتائج تحليل التباين (ANOVA) المتداخل ويؤكد أن الأسمدة لها تأثير كبير على نمو النبات، ولكن الفنيين الأفراد لا يفعلون ذلك.

مصادر إضافية

كيفية إجراء ANOVA أحادي الاتجاه في R
كيفية إجراء ANOVA ثنائي الاتجاه في R
كيفية تنفيذ التدابير المتكررة ANOVA في R