أنوفا مقابل الانحدار: ما هو الفرق؟
هناك نموذجان شائعان الاستخدام في الإحصائيات هما ANOVA ونماذج الانحدار.
يشترك هذان النوعان من النماذج في التشابه التالي:
- متغير الاستجابة في كل نموذج مستمر. تتضمن أمثلة المتغيرات المستمرة الوزن والطول والطول والعرض والوقت والعمر وما إلى ذلك.
ومع ذلك، فإن هذين النوعين من النماذج يشتركان في الفرق التالي:
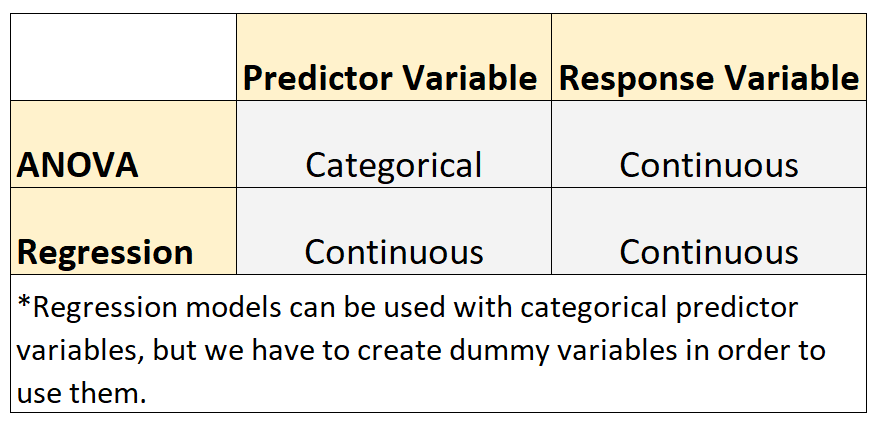
- يتم استخدام نماذج ANOVA عندما تكون متغيرات التوقع قاطعة. تشمل أمثلة المتغيرات الفئوية مستوى التعليم ولون العين والحالة الاجتماعية وما إلى ذلك.
- تُستخدم نماذج الانحدار عندما تكون متغيرات التوقع مستمرة.*
*يمكن استخدام نماذج الانحدار مع متغيرات التوقع الفئوية، ولكننا نحتاج إلى إنشاء متغيرات وهمية لاستخدامها.
توضح الأمثلة التالية متى يتم استخدام ANOVA أو نماذج الانحدار عمليًا.
مثال 1: نموذج ANOVA المفضل
لنفترض أن عالم الأحياء يريد أن يفهم ما إذا كانت أربعة أسمدة مختلفة تؤدي إلى نفس متوسط نمو النبات (بالبوصة) خلال فترة شهر واحد أم لا. ولاختبار ذلك، قامت بتطبيق كل سماد على 20 نباتًا وسجلت نمو كل نبات بعد شهر.
في هذا السيناريو، يجب على عالم الأحياء استخدام نموذج ANOVA أحادي الاتجاه لتحليل الاختلافات بين الأسمدة نظرًا لوجود متغير متنبئ وهو متغير قاطع.
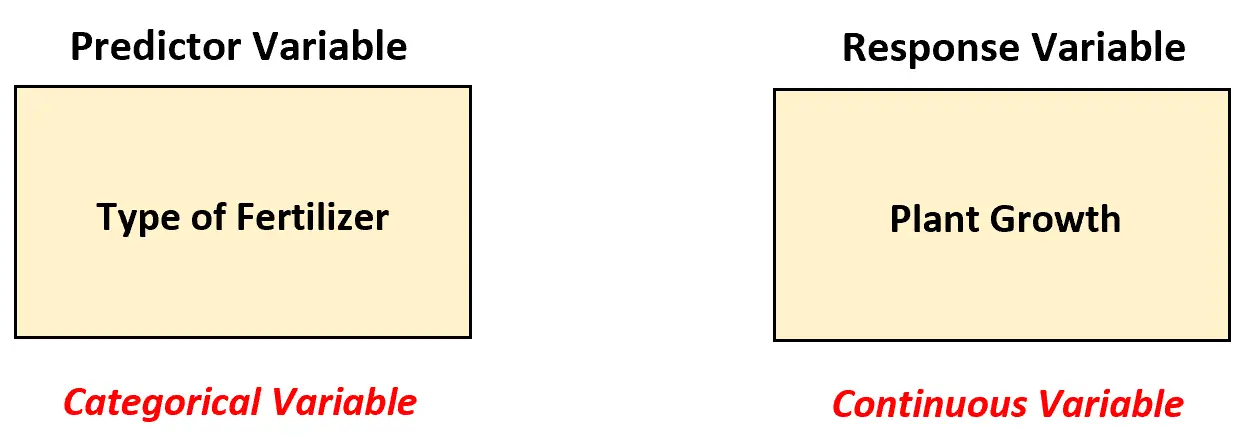
بمعنى آخر، يمكن تصنيف قيم المتغير المتنبئ إلى “الفئات” التالية:
- الأسمدة 1
- الأسمدة 2
- الأسمدة 3
- الأسمدة 4
سوف يخبر ANOVA أحادي الاتجاه عالم الأحياء ما إذا كان متوسط نمو النبات متساويًا بين الأسمدة الأربعة المختلفة أم لا.
المثال 2: نموذج الانحدار المفضل
لنفترض أن وكيلًا عقاريًا يريد فهم العلاقة بين اللقطات المربعة وسعر العقار. ولتحليل هذه العلاقة، قام بجمع بيانات عن المساحة بالقدم المربع وسعر 200 منزل في مدينة معينة.
في هذا السيناريو، يجب على الوكيل العقاري استخدام نموذج انحدار خطي بسيط لتحليل العلاقة بين هذين المتغيرين لأن المتغير المتوقع (القدم المربع) مستمر.
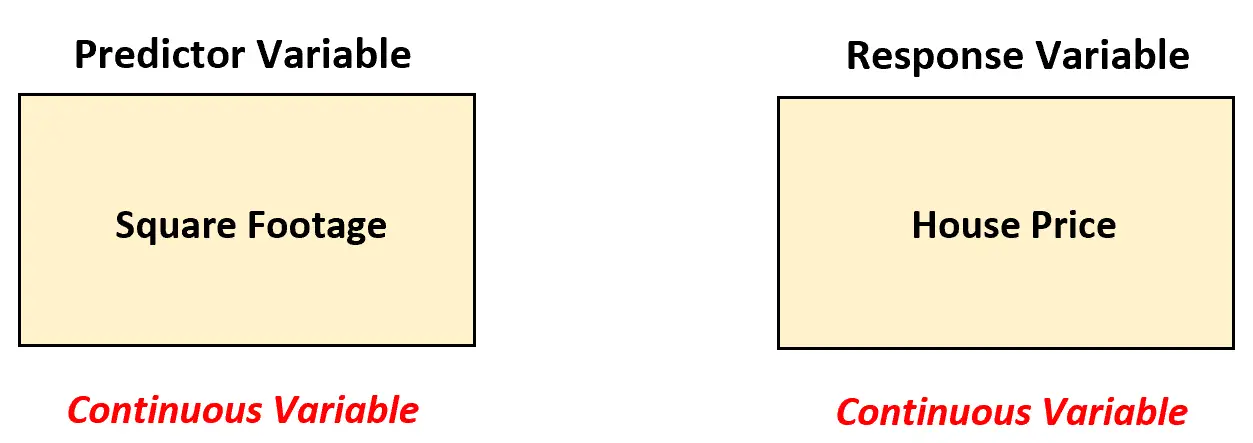
باستخدام الانحدار الخطي البسيط، يمكن للوكيل العقاري أن يناسب نموذج الانحدار التالي:
سعر العقار = β 0 + β 1 (مساحة مربعة)
ستمثل قيمة β 1 متوسط التغير في سعر المنزل المرتبط بكل قدم مربع إضافي.
سيسمح هذا للوكيل العقاري بتحديد العلاقة بين اللقطات المربعة وسعر العقار.
مثال 3: نموذج الانحدار مع المتغيرات الوهمية المفضلة
لنفترض أن وكيل عقاري يريد فهم العلاقة بين المتغيرات المتنبئة “اللقطة المربعة” و”نوع المنزل” (عائلة واحدة، شقة، منزل مستقل) مع متغير الاستجابة لسعر العقار.
في هذا السيناريو، يمكن للوكيل العقاري استخدام الانحدار الخطي المتعدد عن طريق تحويل “نوع المنزل” إلى متغير وهمي لأنه متغير فئوي حاليًا.
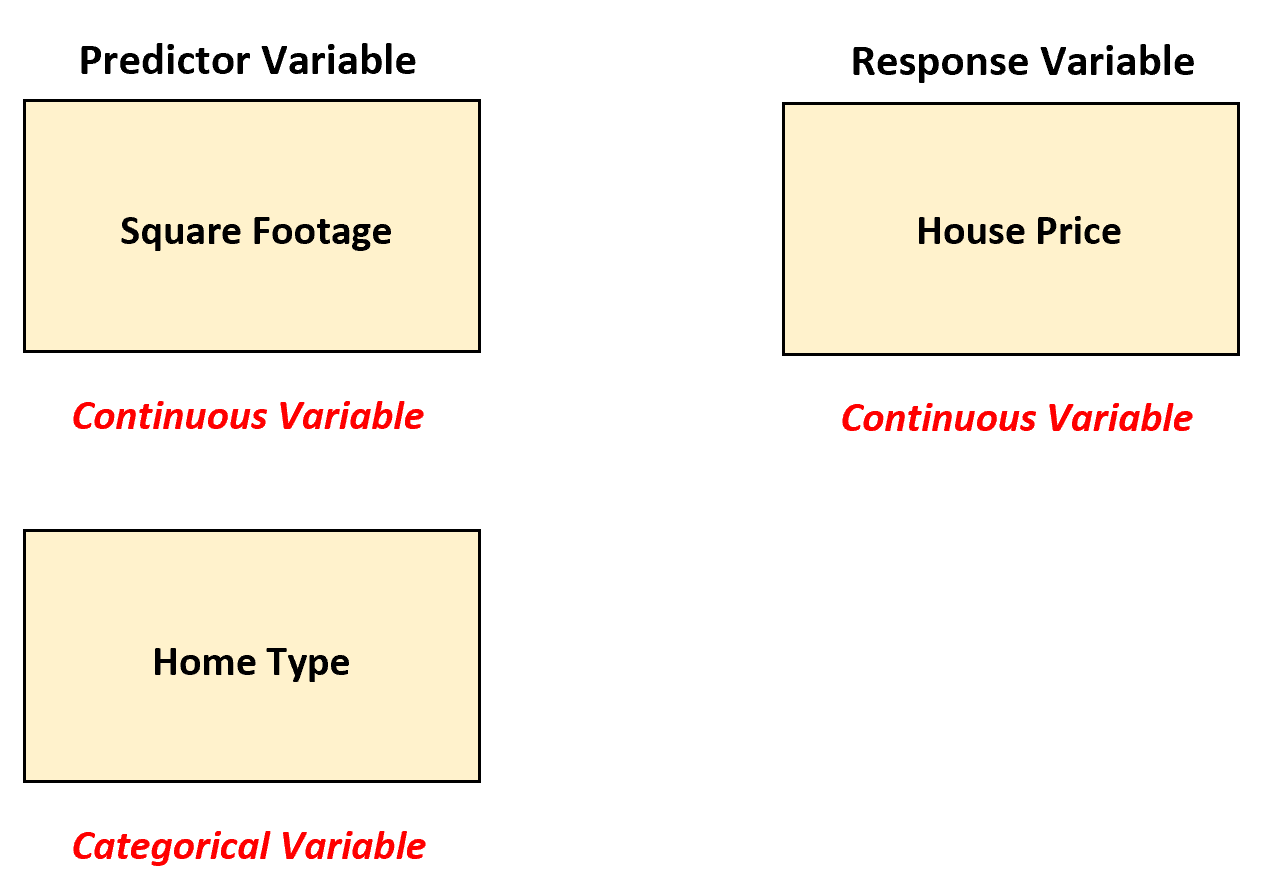
يمكن للوكيل العقاري بعد ذلك أن يلائم نموذج الانحدار الخطي المتعدد التالي:
سعر العقار = β 0 + β 1 (مساحة مربعة) + β 2 (عائلة واحدة) + β 3 (شقة)
إليك كيفية تفسير معاملات النموذج:
- β 1 : متوسط التغير في سعر المنزل المرتبط بقدم مربع إضافي واحد.
- β 2 : متوسط فرق السعر بين منزل الأسرة الواحدة والمنزل المستقل، بافتراض أن المساحة المربعة تظل ثابتة.
- β 3 : متوسط فرق السعر بين منزل الأسرة الواحدة والشقة، بافتراض أن مساحة السطح ثابتة.
راجع البرامج التعليمية التالية لمعرفة كيفية إنشاء متغيرات وهمية في برامج إحصائية مختلفة:
مصادر إضافية
توفر البرامج التعليمية التالية مقدمة متعمقة لنماذج ANOVA:
توفر البرامج التعليمية التالية مقدمة متعمقة لنماذج الانحدار الخطي:
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر