كيفية العثور على احتمال مع المتوسط والانحراف المعياري

يمكننا استخدام العملية التالية لإيجاد احتمال وجود متغير عشوائي موزع بشكل طبيعي

الخطوة 1: ابحث عن درجة z.

تخبرك النتيجة z بعدد الانحرافات المعيارية التي تقع قيمة البيانات الفردية عن المتوسط. يتم حسابه على النحو التالي:

النتيجة z = (x – μ) / σ

ذهب:

• x: قيمة البيانات الفردية
• μ: متوسط عدد السكان
• σ : الانحراف المعياري للسكان

الخطوة 2: ابحث عن الاحتمال الذي يتوافق مع درجة z.

بمجرد أن نحسب النتيجة z، يمكننا إيجاد الاحتمالية المقابلة لها في الجدول z.

توضح الأمثلة التالية كيفية استخدام هذه العملية في سيناريوهات مختلفة.

مثال 1: الاحتمال أقل من قيمة معينة

يتم توزيع الدرجات في اختبار معين عادةً بمتوسط μ = 82 والانحراف المعياري σ = 8. ما احتمال أن يحصل طالب معين على درجات أقل من 84 في الاختبار؟

الخطوة 1: ابحث عن درجة z.

أولاً، سوف نجد درجة z المرتبطة بنتيجة 84:

النتيجة z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0.25

الخطوة 2: استخدم الجدول z للعثور على الاحتمال المقابل.

بعد ذلك، سوف نبحث عن القيمة 0.25 في الجدول z:

احتمال أن يسجل طالب ما أقل من 84 هو 59.87% تقريبًا.

مثال 2: الاحتمال أكبر من قيمة معينة

يتم توزيع ارتفاع نوع معين من طيور البطريق عادةً بمتوسط μ = 30 بوصة وانحراف معياري قدره σ = 4 بوصات. إذا اخترنا بطريقًا عشوائيًا، فما احتمال أن يزيد طوله عن 28 بوصة؟

الخطوة 1: ابحث عن درجة z.

أولاً، سنجد درجة z المرتبطة بارتفاع 28 بوصة.

النتيجة ض = (س – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0.5

الخطوة 2: استخدم الجدول z للعثور على الاحتمال المقابل.

بعد ذلك سوف نبحث عن القيمة -0.5   في الجدول ض:

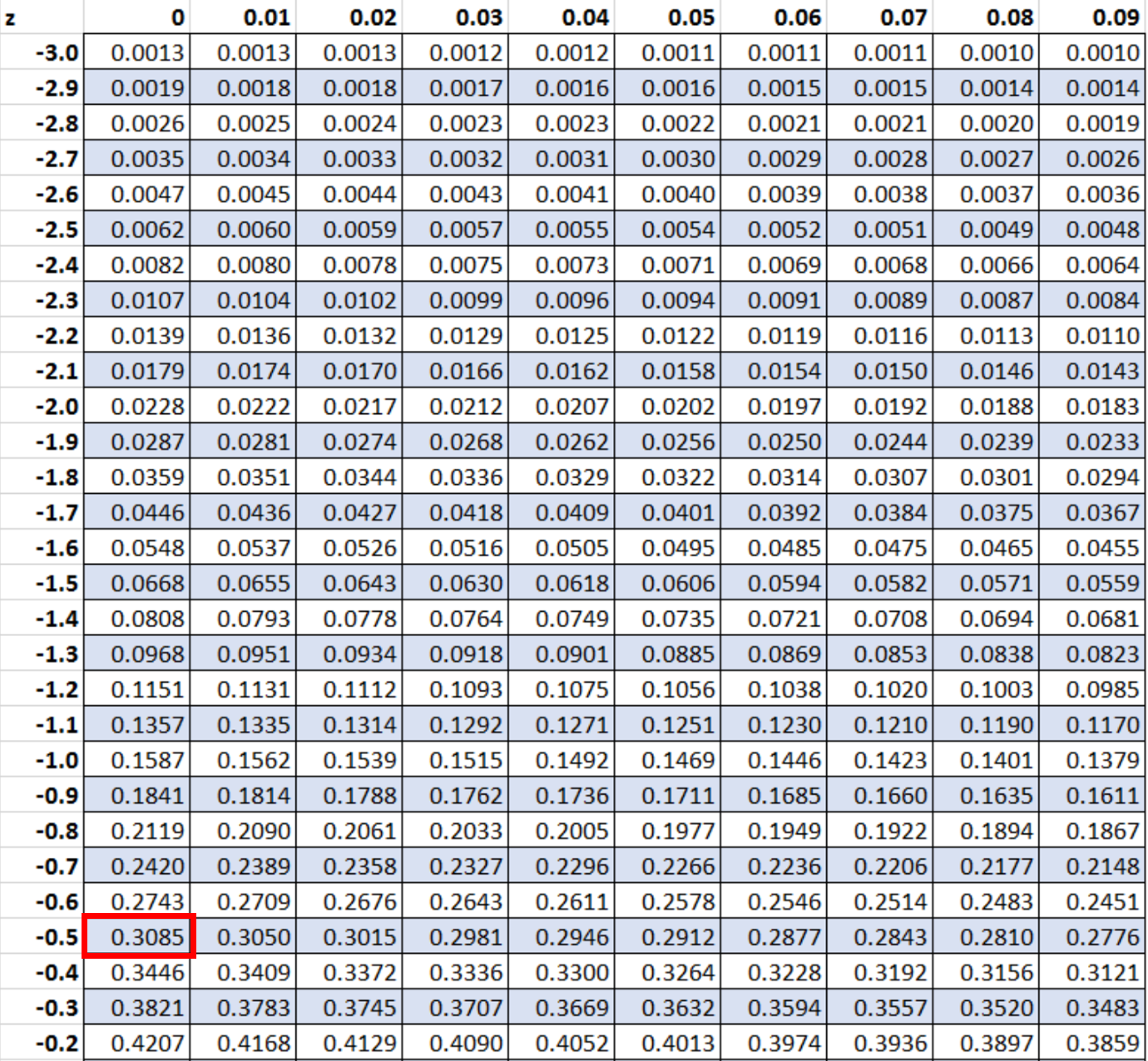
القيمة التي تقابل درجة z تبلغ -0.5 هي 0.3085. يمثل هذا احتمال أن يكون طول البطريق أقل من 28 بوصة.

ومع ذلك، بما أننا نريد معرفة احتمال أن يكون طول البطريق أكثر من 28 بوصة، فإننا نحتاج إلى طرح هذا الاحتمال من 1.

لذا فإن احتمال أن يكون طول البطريق أكثر من 28 بوصة هو: 1 – 0.3085 = 0.6915 .

مثال 3: الاحتمال بين قيمتين

يتم توزيع وزن نوع معين من السلاحف عادةً بمتوسط μ = 400 رطل وانحراف معياري قدره σ = 25 رطلاً. إذا اخترنا سلحفاة عشوائيًا، فما احتمال أن يتراوح وزنها بين 410 و425 رطلاً؟

الخطوة 1: ابحث عن نتائج z.

أولاً، سنجد درجات z المرتبطة بـ 410 كتابًا و425 كتابًا

النتيجة z 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0.4

درجة ض 425 = (س – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

الخطوة 2: استخدم الجدول z للعثور على الاحتمال المقابل.

أولاً، سوف نبحث عن القيمة 0.4   في الجدول ض:

بعد ذلك سوف نبحث عن القيمة 1   في الجدول ض:

بعد ذلك، سنطرح القيمة الأصغر من القيمة الأكبر: 0.8413 – 0.6554 = 0.1859 .

لذا فإن احتمال أن يكون وزن السلحفاة التي تم اختيارها عشوائيًا بين 410 رطلاً و425 رطلاً هو 18.59% .

مصادر إضافية

كيفية حساب قيمة P يدويًا من درجة Z
كيفية تحويل درجات Z إلى درجات أولية
كيفية العثور على درجات Z في منطقة معينة