دليل لإجراءات بنياميني-هوخبيرج

في أي وقت تقوم فيه بإجراء اختبار إحصائي، من الممكن أن تحصل على قيمة p أقل من 0.05 بالصدفة البحتة، حتى لو كانت فرضيتك الصفرية صحيحة.

على سبيل المثال، لنفترض أنك تريد معرفة ما إذا كان متوسط ارتفاع نبات معين أكبر من 10 بوصات. ستكون فرضياتك الفارغة والبديلة للاختبار هي:

ح ₀ : μ = 10 بوصة

ح _أ : μ > 10 بوصات

ولاختبار هذه الفرضية، يمكنك الخروج وجمع عينة عشوائية من 20 نباتًا لقياسها. على الرغم من أن متوسط الارتفاع الحقيقي لهذا النوع من النباتات هو 10 بوصات، فمن الممكن أنك قمت باختيار عينة من 20 نباتًا طويل القامة بشكل غير عادي، مما يؤدي إلى رفض فرضية العدم.

حتى لو كانت فرضية العدم صحيحة (كان متوسط ارتفاع هذا النبات في الواقع 10 بوصات)، فإنك رفضتها. في الإحصائيات، نسمي هذا “الاكتشاف الزائف”. أنت تدعي أنك توصلت إلى اكتشاف – “نتيجة مهمة” – لكن هذا في الواقع غير صحيح.

تخيل الآن إجراء 100 اختبار إحصائي في وقت واحد. باستخدام مستوى ألفا قدره 0.05، هناك فرصة بنسبة 5% فقط لتحقيق اكتشاف خاطئ من خلال اختبار فردي، ولكن نظرًا لأنك تقوم بهذا العدد الكبير من الاختبارات، فإنك تتوقع أن يؤدي 5 فقط من أصل 100 إلى اكتشافات خاطئة.

في العالم الحديث، يمكن أن تكون الاكتشافات الخاطئة مشكلة شائعة لأن التكنولوجيا أتاحت للباحثين إجراء مئات أو حتى آلاف الاختبارات الإحصائية في وقت واحد.

على سبيل المثال، يمكن للباحثين الطبيين إجراء اختبارات إحصائية على عشرات الآلاف من الجينات في المرة الواحدة. وحتى مع معدل اكتشاف خاطئ يبلغ 5% فقط، فهذا يعني أن مئات الاختبارات قد تؤدي إلى اكتشافات خاطئة.

إحدى طرق التحكم في معدل الاكتشافات الكاذبة هي استخدام ما يسمى بإجراء بنياميني-هوخبيرج.

إجراء بنياميني-هوخبيرج

يعمل إجراء بنياميني-هوخبيرج على النحو التالي:

الخطوة 1: قم بإجراء جميع اختباراتك الإحصائية وابحث عن القيمة الاحتمالية لكل اختبار.

الخطوة 2: قم بترتيب القيم الاحتمالية بترتيب تنازلي، مع تعيين رتبة لكل واحدة: أصغر قيمة لها رتبة 1، والقيمة الأصغر التالية لها رتبة 2، وما إلى ذلك.

الخطوة 3: حساب قيمة بنياميني-هوخبيرج الحرجة لكل قيمة p، باستخدام الصيغة (i/m)*Q

ذهب:

i = رتبة القيمة p

م = العدد الإجمالي للاختبارات

س = معدل الاكتشاف الكاذب الذي اخترته

الخطوة 4: ابحث عن أكبر قيمة p أقل من القيمة الحرجة. قم بتعيين كل قيمة p أقل من هذه القيمة p على أنها مهمة.

يوضح المثال التالي كيفية تنفيذ هذا الإجراء بقيم محددة.

مثال

لنفترض أن الباحثين يريدون تحديد ما إذا كان هناك 20 متغيرًا مختلفًا مرتبطة بأمراض القلب أم لا. يقومون بإجراء 20 اختبارًا إحصائيًا فرديًا في المرة الواحدة ويحصلون على قيمة p لكل اختبار. ويبين الجدول التالي القيم الاحتمالية لكل اختبار، مرتبة تنازلياً.

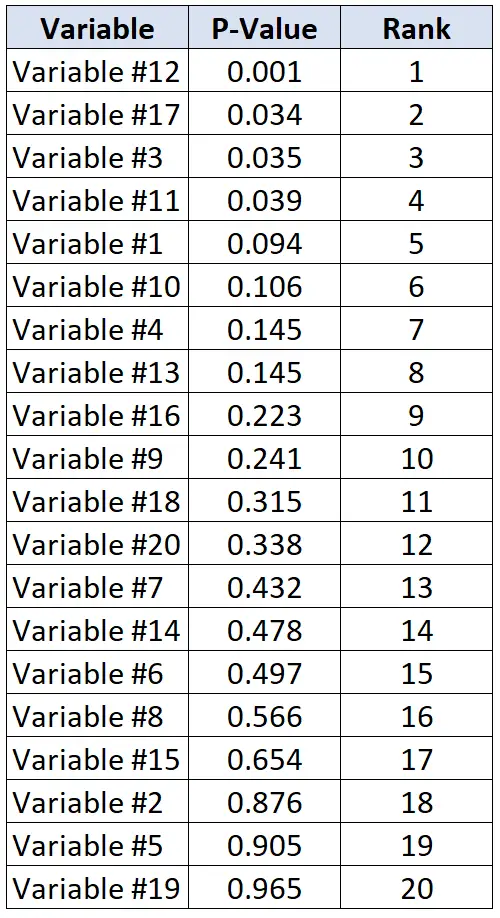
لنفترض أن الباحثين على استعداد لقبول معدل اكتشاف كاذب قدره 20%. لذلك، لحساب قيمة بنياميني-هوخبيرج الحرجة لكل قيمة p، يمكننا استخدام الصيغة التالية: (i/20)*0.2 حيث i = رتبة القيمة p.

يوضح الجدول التالي قيمة Benjamini-Hochberg الحرجة لكل قيمة p فردية:

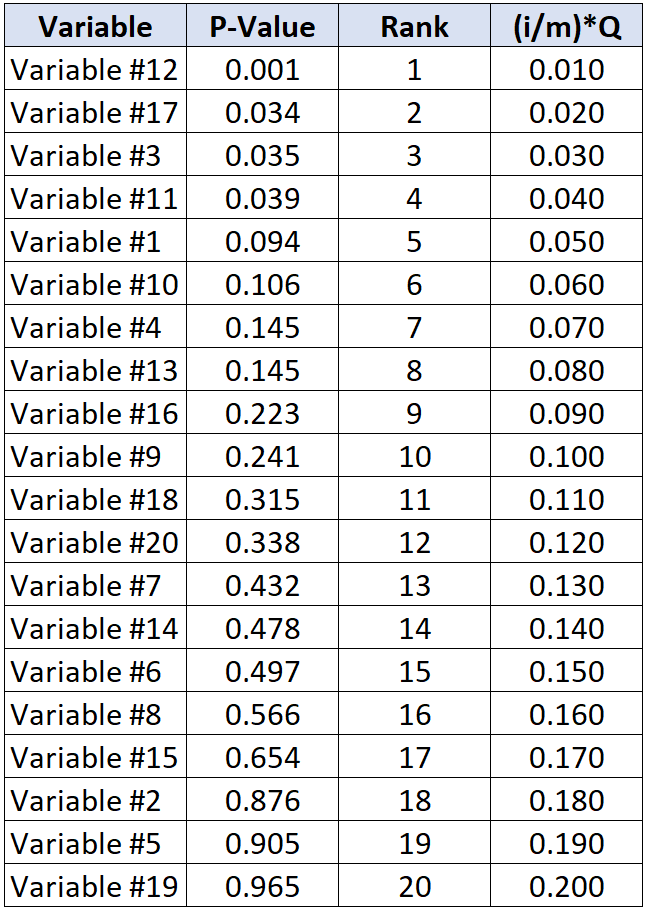
الاختبار ذو أكبر قيمة p أقل من قيمته الحرجة Benjamini-Hochberg هو المتغير رقم 11، الذي له قيمة p تبلغ 0.039 وقيمة BH الحرجة تبلغ 0.040.

وبالتالي، فإن هذا الاختبار وجميع الاختبارات ذات القيمة p الأصغر ستعتبر ذات أهمية.

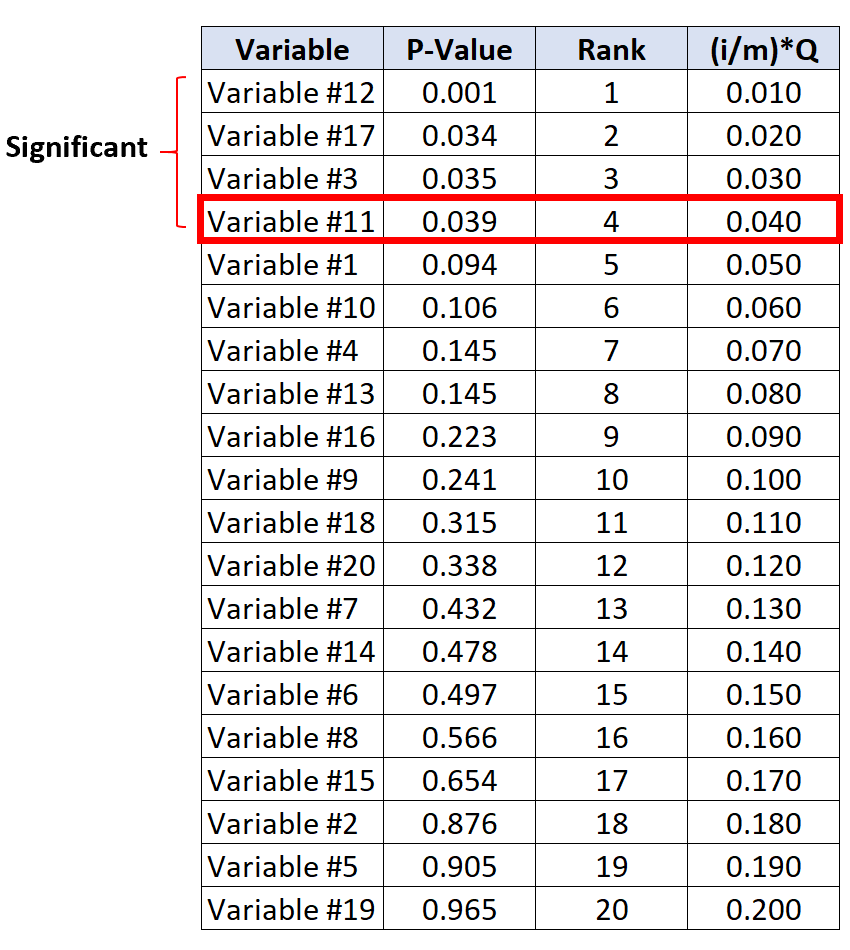
لاحظ أنه على الرغم من أن المتغيرين رقم 17 ورقم 3 لا يحتويان على قيم p أصغر من قيم BH الحرجة الخاصة بهما، إلا أنهما ما زالا يعتبران مهمين لأن لديهما قيم p أصغر من المتغير رقم 11.

كيفية اختيار معدل اكتشاف كاذب

إحدى أهم الخطوات في إجراء بنياميني-هوخبيرج هي اختيار معدل اكتشاف خاطئ. يجب عليك اختيار معدل الاكتشاف الكاذب الخاص بك قبل جمع البيانات أو إجراء الاختبارات الإحصائية.

عادةً، ستقوم بإجراء عدد كبير من الاختبارات الإحصائية خلال المرحلة الاستكشافية لتحليلك، والتي ستتبعها بعد ذلك باختبارات أخرى لاستكشاف نتائجك بشكل أكبر.

إذا كان اختبار المتابعة غير مكلف، فقد تفكر في تحديد معدل اكتشاف خاطئ أعلى، لأنه حتى لو كان لديك بعض الاكتشافات الخاطئة، فمن المحتمل أن تكتشف تلك الاكتشافات الخاطئة في الاختبارات اللاحقة.

بالإضافة إلى ذلك، إذا كانت تكلفة تفويت اكتشاف مهم مرتفعة، فقد ترغب في زيادة معدل الاكتشاف الزائف حتى لا يفوتك أي شيء مهم.

اعتمادًا على تكاليف بحثك وأهمية عدم تفويت أي نتائج مهمة، فإن معدل الاكتشاف الكاذب سيختلف من حالة إلى أخرى.

مصادر إضافية

شرح القيم P والأهمية الإحصائية
ما هو معدل الخطأ لكل عائلة؟