ما هي دالة الكتلة الاحتمالية (pmf) في الإحصاء؟

تخبرنا دالة الكتلة الاحتمالية ، والتي غالبًا ما يتم اختصارها بـ PMF ، باحتمال أن يأخذ المتغير العشوائي المنفصل قيمة معينة.

على سبيل المثال، لنفترض أننا ألقينا حجر النرد مرة واحدة. إذا تركنا x تشير إلى الرقم الذي يقع عليه النرد، فيمكن وصف احتمال أن تكون x مساوية لقيم مختلفة على النحو التالي:

• ف(س = 1): 1/6
• ف(س = 2): 1/6
• ف(س = 3): 1/6
• ف(س = 4): 1/6
• ف(س = 5): 1/6
• ف(س = 6): 1/6

هناك فرصة متساوية أن يستقر النرد على أي رقم يقع بين 1 و 6.

إليك كيفية كتابة هذه الاحتمالات كدالة احتمالية جماعية:

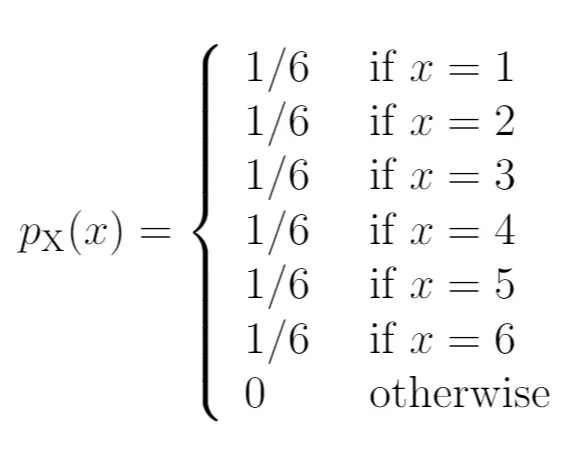
يوضح الجانب الأيسر من الرسم البياني الاحتمالية المرتبطة بالنتائج الموجودة على الجانب الأيمن:

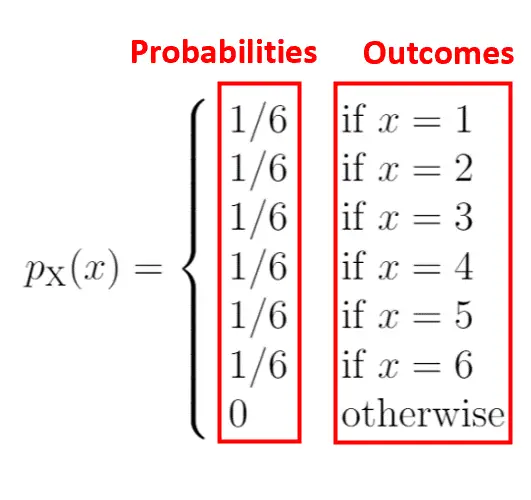
من خصائص دالة الكتلة الاحتمالية أن جميع الاحتمالات يجب أن يكون مجموعها 1. ستلاحظ أن PMF هذا يستوفي هذا الشرط:

مجموع الاحتمالات = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

يشير دعم دالة الكتلة الاحتمالية إلى مجموعة القيم التي يمكن أن يأخذها المتغير العشوائي المنفصل. في هذا المثال، سيكون الدعم {1، 2، 3، 4، 5، 6} نظرًا لأن قيمة القالب يمكن أن تأخذ أيًا من هذه القيم.

خارج نطاق الدعم، تكون قيمة PMF صفرًا. على سبيل المثال، احتمال سقوط النرد على الرقم “0” أو “7” أو “8” هو صفر نظرًا لعدم تضمين أي من هذه الأرقام في القوس.

وظائف الكتلة الاحتمالية في الممارسة العملية

المثالان الأكثر شيوعًا لوظائف الكتلة الاحتمالية في الممارسة العملية يتعلقان بالتوزيع ذي الحدين وتوزيع بواسون .

توزيع ثنائي

إذا كان المتغير العشوائي X يتبع التوزيع ذي الحدين، فيمكن العثور على احتمال نجاح X = k من خلال الصيغة التالية:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ذهب:

• ن: عدد التجارب
• ك: عدد النجاحات
• ع: احتمال النجاح في تجربة معينة
• _n C _k : عدد الطرق للحصول على نجاحات k في التجارب n

على سبيل المثال، لنفترض أننا نقلب عملة معدنية 3 مرات. يمكننا استخدام الصيغة أعلاه لتحديد احتمالية الحصول على 0 و1 و2 و3 رؤوس في هذه الرميات الثلاث:

• ف(X=0) = ₃ ج ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125
• ف(X=1) = ₃ ج ₁ * 0.5 ¹ * (1-0.5) ^3-1 = 1 * 1 * (0.5) ² = 0.375
• ف(X=2) = ₃ ج ₂ * 0.5 ² * (1-0.5) ^3-2 = 1 * 1 * (0.5) ¹ = 0.375
• ف(X=3) = ₃ ج ₃ * 0.5 ³ * (1-0.5) ^3-3 = 1 * 1 * (0.5) ⁰ = 0.125

توزيع الأسماك

إذا كان المتغير العشوائي X يتبع توزيع بواسون، فيمكن العثور على احتمال نجاح X = k من خلال الصيغة التالية:

P(X=k) =  ^ك * ه ^{– } / ك!

ذهب:

• : متوسط عدد النجاحات التي تحدث خلال فترة زمنية محددة
• ك: عدد النجاحات
• e: ثابت يساوي 2.71828 تقريبًا

على سبيل المثال، لنفترض أن مستشفى معين يشهد معدل ولادتين في الساعة. يمكننا استخدام الصيغة أعلاه لتحديد احتمالية حدوث 0، 1، 2، 3 ولادات، وما إلى ذلك. في ساعة معينة:

• P(X=0) = 2 ⁰ * ه ^{– 2} / 0! = 0.1353
• P(X=1) = 2 ¹ * ه ^{– 2} / 1! = 0.2707
• ع(X=2) = 2 ² * ه ^{– 2} / 2! = 0.2707
• ع(X=3) = 2 ³ * ه ^{– 2} / 3! = 0.1805

عرض PMF

غالبًا ما نتصور الدوال الجماعية الاحتمالية باستخدام الرسوم البيانية الشريطية.

على سبيل المثال، يوضح الرسم البياني الشريطي التالي الاحتمالات المرتبطة بعدد الولادات في الساعة لتوزيع بواسون الموضح في المثال السابق:

لاحظ أن عدد الولادات يمكن أن يمتد إلى ما لا نهاية، لكن الاحتمالات تصبح صغيرة جدًا بعد 10 بحيث لا يمكنك حتى رؤيتها على الرسم البياني الشريطي.

خصائص PMF

دالة الكتلة الاحتمالية لها الخصائص التالية:

1. كل الاحتمالات إيجابية في التأييد. على سبيل المثال، احتمال سقوط حجر النرد بين 1 و6 يكون موجبًا، في حين أن احتمال جميع النتائج الأخرى يكون صفرًا.

2. جميع النتائج لها احتمال بين 0 و1. على سبيل المثال، احتمال سقوط حجر النرد بين 1 و6 هو 1/6، أو 0.1666666 لكل نتيجة.

3. مجموع كل الاحتمالات يجب أن يساوي 1. على سبيل المثال، مجموع احتمالات سقوط حجر نرد على رقم معين هو 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.

مصادر إضافية

ما هي المتغيرات العشوائية؟
CDF أو PDF: ما الفرق؟
مقدمة للتوزيع ذي الحدين
مقدمة لتوزيع بواسون