كيفية إنشاء مخططات متغيرة ملحقة في r

في الإحصائيات، تعد المخططات المتغيرة المضافة عبارة عن مخططات فردية تعرض العلاقة بين متغير الاستجابة ومتغير التوقع في نموذج الانحدار الخطي المتعدد، مع التحكم في وجود متغيرات توقع أخرى في النموذج.

ملاحظة: في بعض الأحيان تسمى هذه المخططات أيضًا “مخططات الانحدار الجزئي”.

يتيح لنا هذا النوع من المخططات ملاحظة العلاقة بين كل متغير متنبئ فردي ومتغير الاستجابة في النموذج مع الحفاظ على ثبات متغيرات التنبؤ الأخرى.

لإنشاء مخططات للمتغيرات الملحقة في لغة R، يمكننا استخدام الدالة avPlots() من الحزمة car :

 #load car package
library (car) 

#fit multiple linear regression model
model <- lm(y ~ x1 + x2 + ..., data = df)

#create added variable plots
avPlots(model)

يوضح المثال التالي كيفية استخدام بناء الجملة هذا عمليًا.

مثال: إضافة قطع أرض متغيرة في R

لنفترض أننا نلائم نموذج الانحدار الخطي المتعدد التالي في R، باستخدام بيانات من مجموعة بيانات mtcars :

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view summary of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

لتصور العلاقة بين متغير الاستجابة “mpg” وكل متغير توقع فردي في النموذج، يمكننا إنتاج مخططات للمتغيرات المضافة باستخدام الدالة avPlots() :

 #load car package
library (car)

#produce added variable plots
avPlots(model)

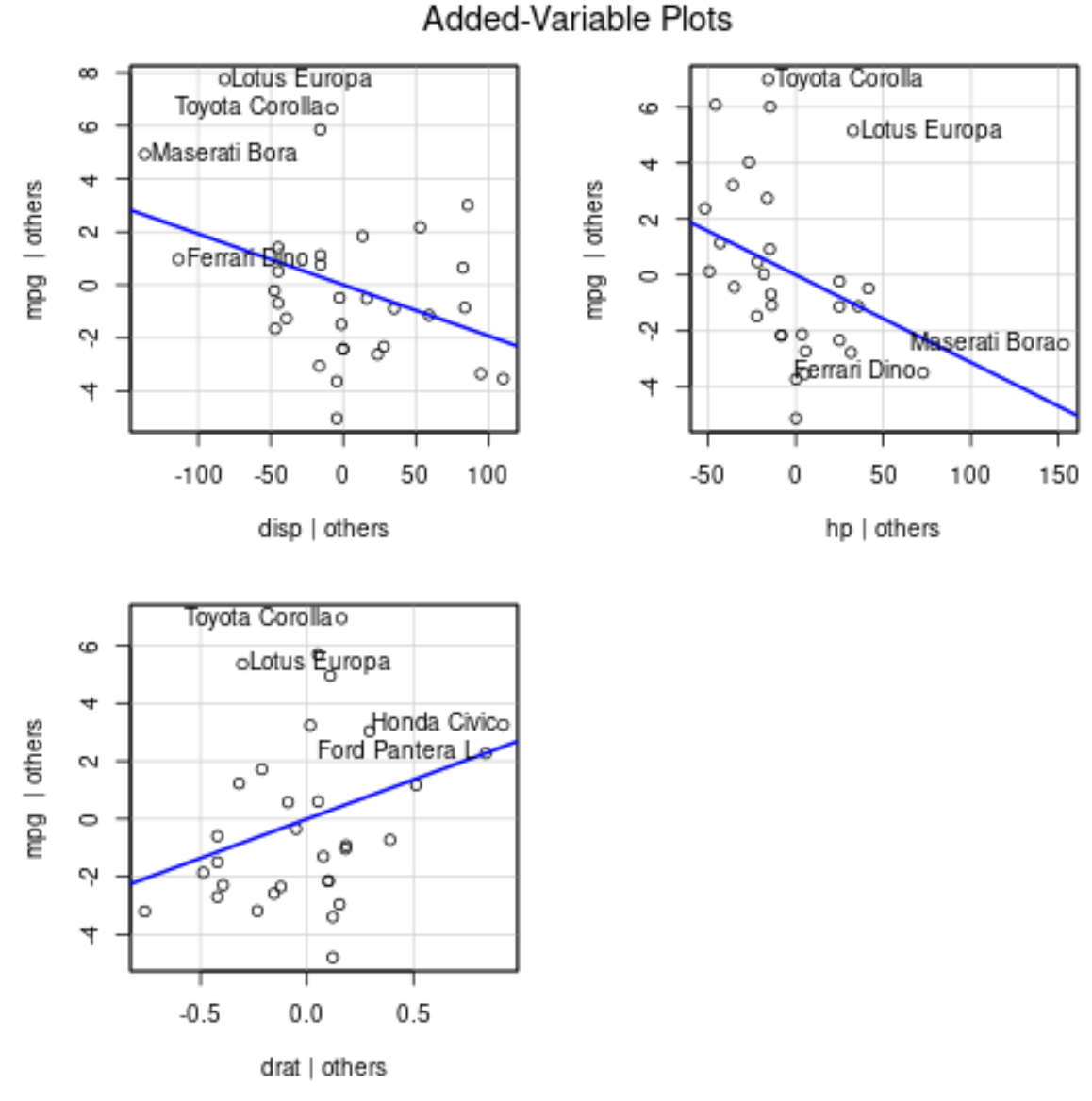
وإليك كيفية تفسير كل مؤامرة:

• يعرض المحور السيني متغيرًا متوقعًا واحدًا ويعرض المحور الصادي متغير الاستجابة.
• يوضح الخط الأزرق الارتباط بين متغير التوقع ومتغير الاستجابة، مع الحفاظ على قيمة جميع متغيرات التوقع الأخرى ثابتة .
• تمثل النقاط المسماة في كل رسم بياني الملاحظتين اللتين تحتويان على أكبر القيم المتبقية والملاحظتين اللتين تتمتعان بأكبر نفوذ جزئي.

لاحظ أن زاوية الخط في كل مخطط تتوافق مع إشارة معامل معادلة الانحدار المقدرة.

على سبيل المثال، فيما يلي المعاملات المقدرة لكل متغير متنبئ في النموذج:

• العرض: -0.019232
• الفصل: -0.031229
• التاريخ: 2.714975

لاحظ أن زاوية الخط موجبة في المخطط المتغير المضاف لـ drt بينما تكون سالبة لـ disp و hp ، وهو ما يتوافق مع إشارات معاملاتهما المقدرة:

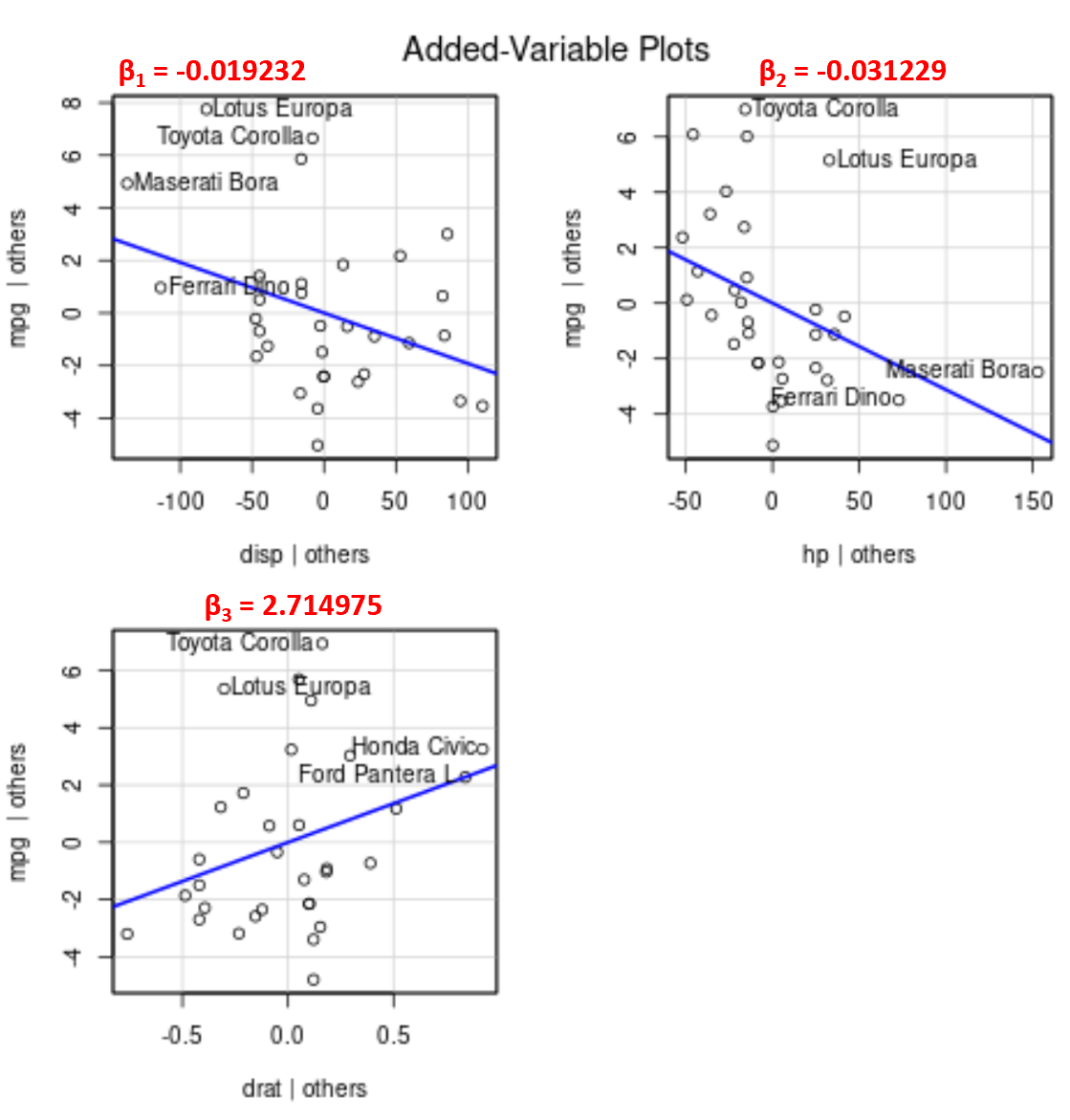
تسمح لنا هذه الرسوم البيانية بتصور العلاقة بين كل متغير متنبئ فردي ومتغير الاستجابة بسهولة.

مصادر إضافية

كيفية إجراء الانحدار الخطي البسيط في R
كيفية إجراء الانحدار الخطي المتعدد في R
كيفية إجراء الانحدار اللوجستي في R