كيفية استخدام التوزيع الهندسي في إكسل

يصف التوزيع الهندسي احتمالية مواجهة عدد معين من حالات الفشل قبل تجربة النجاح الأول في سلسلة من تجارب برنولي.

تجربة برنولي هي تجربة ذات نتيجتين محتملتين فقط – “النجاح” أو “الفشل” – واحتمال النجاح هو نفسه في كل مرة يتم فيها إجراء التجربة.

مثال على مقال برنولي هو رمي العملة. لا يمكن للعملة أن تستقر إلا على وجهين (قد نطلق على الصورة “ضربة” والوجه “فشل”) واحتمال النجاح في كل رمية هو 0.5، على افتراض أن العملة عادلة.

إذا كان المتغير العشوائي X يتبع توزيعًا هندسيًا، فيمكن إيجاد احتمالية حدوث حالات فشل k قبل تجربة النجاح الأول من خلال الصيغة التالية:

P(X=k) = (1-p) ^kp

ذهب:

• ك: عدد حالات الفشل قبل النجاح الأول
• ع: احتمال النجاح في كل تجربة

توضح الأمثلة التالية كيفية حساب الاحتمالات المتعلقة بالتوزيع الهندسي في Excel.

مثال 1: اقلب عملة معدنية

لنفترض أننا رمينا قطعة نقود وأردنا معرفة احتمالية حدوث ثلاث “إخفاقات” بالضبط قبل ظهور العملة في النهاية.

سوف نستخدم الصيغة التالية لحساب هذا الاحتمال:

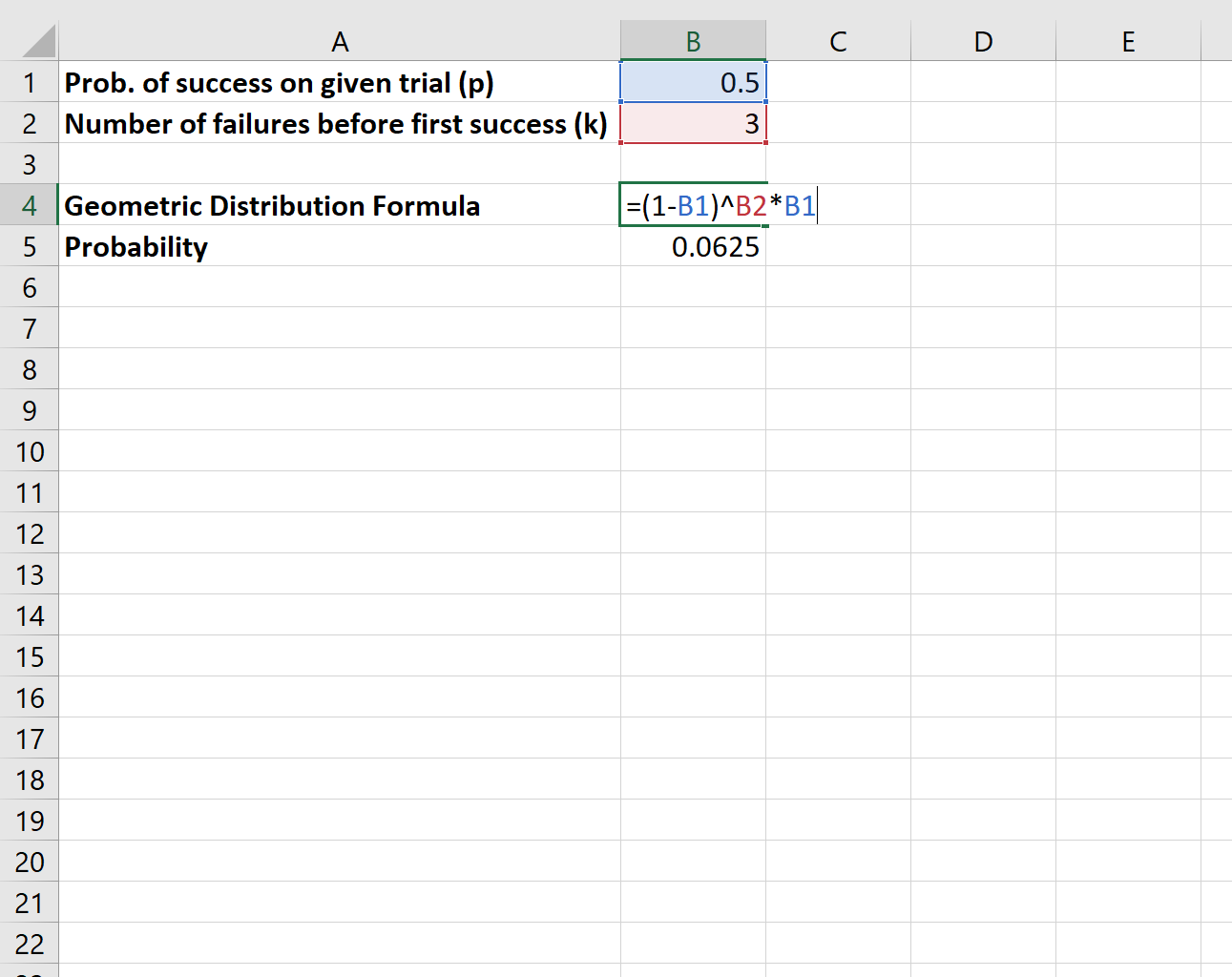
احتمال أن نواجه ثلاث “أخطاء” حتى تظهر العملة أخيرًا هو 0.0625 .

مثال 2: رمية حرة

لنفترض أن لاعب كرة سلة معين ينفذ 60% من رمياته الحرة. ما احتمال أن يضيع اللاعب أربع رميات حرة حتى يسدد واحدة في النهاية؟

سوف نستخدم الصيغة التالية لحساب هذا الاحتمال:

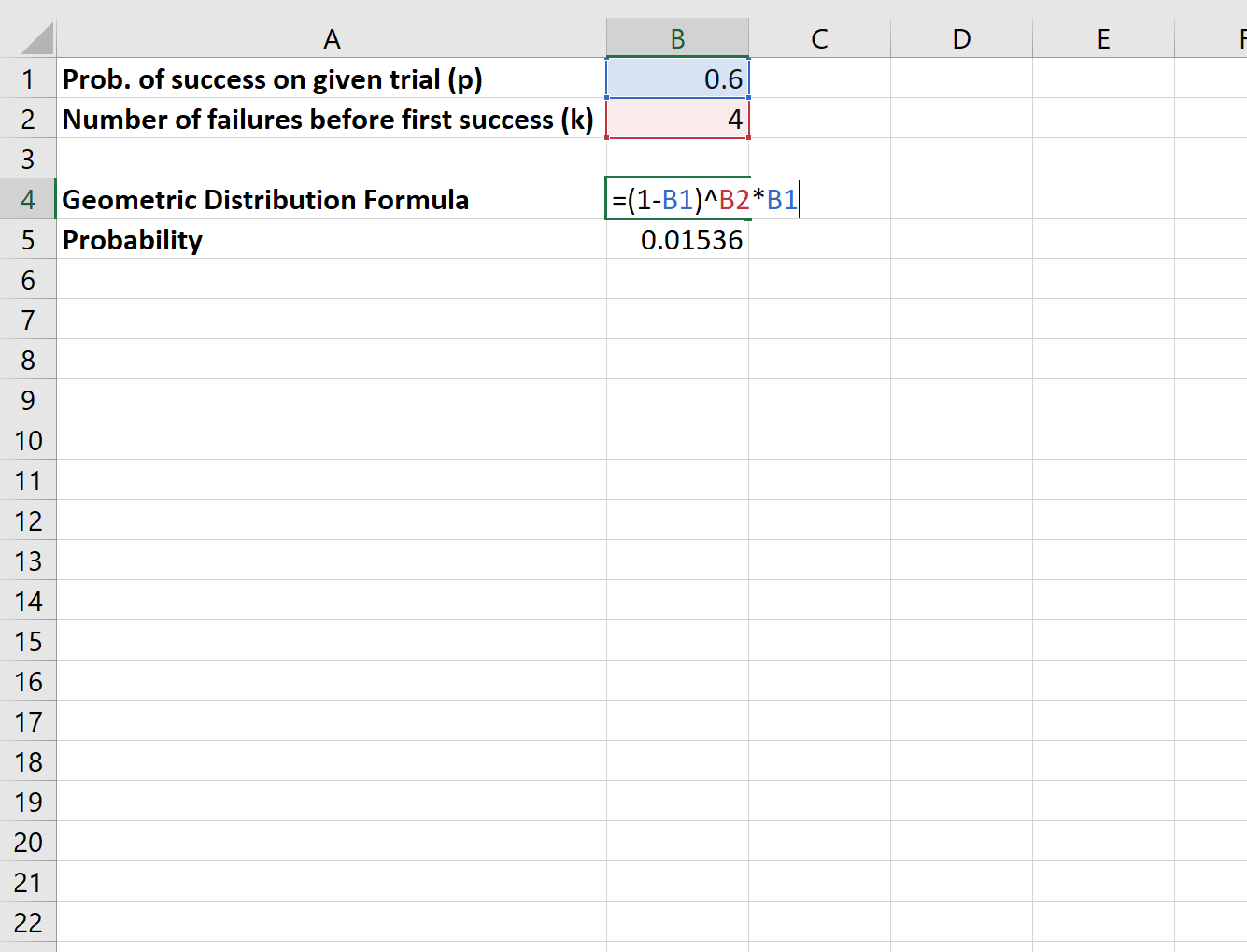
احتمال أن يضيع اللاعب أربع رميات حرة حتى يسدد واحدة في النهاية هو 0.01536 .

مثال 3: دعم القانون

لنفترض أن أحد الباحثين ينتظر خارج إحدى المكتبات ليسأل الأشخاص عما إذا كانوا يدعمون قانونًا معينًا. احتمال أن يدعم شخص ما القانون هو p = 0.2. ما احتمال أن يكون الشخص الرابع الذي يتحدث إليه الباحث هو أول من يؤيد القانون؟

سوف نستخدم الصيغة التالية لحساب هذا الاحتمال:

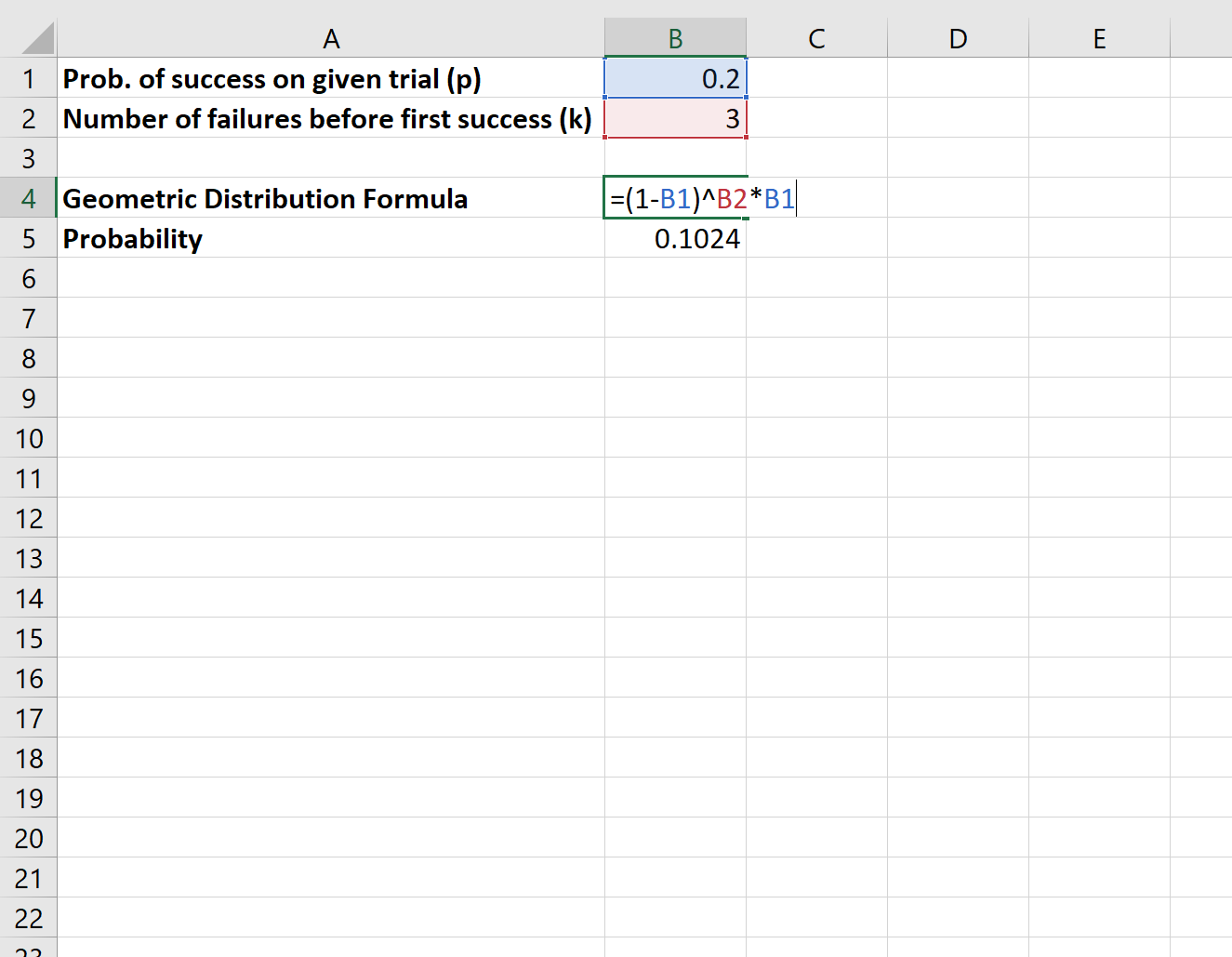
احتمال أن يكون الشخص الرابع الذي يتحدث إليه الباحث هو أول من يؤيد القانون هو 0.1024 .

مصادر إضافية

مقدمة للتوزيع الهندسي
حاسبة التوزيع الهندسي
5 أمثلة ملموسة للتوزيع الهندسي