توزيع برنولي والتوزيع ذي الحدين: ما الفرق؟

يتبع المتغير العشوائي توزيع برنولي إذا كان له نتيجتان محتملتان فقط: 0 أو 1.

على سبيل المثال، لنفترض أننا ألقينا قطعة نقود مرة واحدة. دع ص . وهذا يعني أن احتمال هبوط ذيوله هو 1 – ع .

لذا يمكننا أن نكتب:

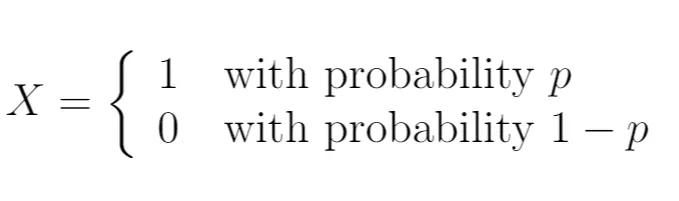
في هذه الحالة، يتبع المتغير العشوائي X توزيع برنولي. يمكن أن يستغرق الأمر قيمتين محتملتين فقط.

الآن، إذا قمنا بقلب عملة معدنية عدة مرات، فإن مجموع متغيرات برنولي العشوائية سيتبع التوزيع ذي الحدين.

على سبيل المثال، لنفترض أننا رمينا عملة معدنية 5 مرات ونريد معرفة احتمال الحصول على الصورة k مرة. يبدو وكأنه متغير عشوائي

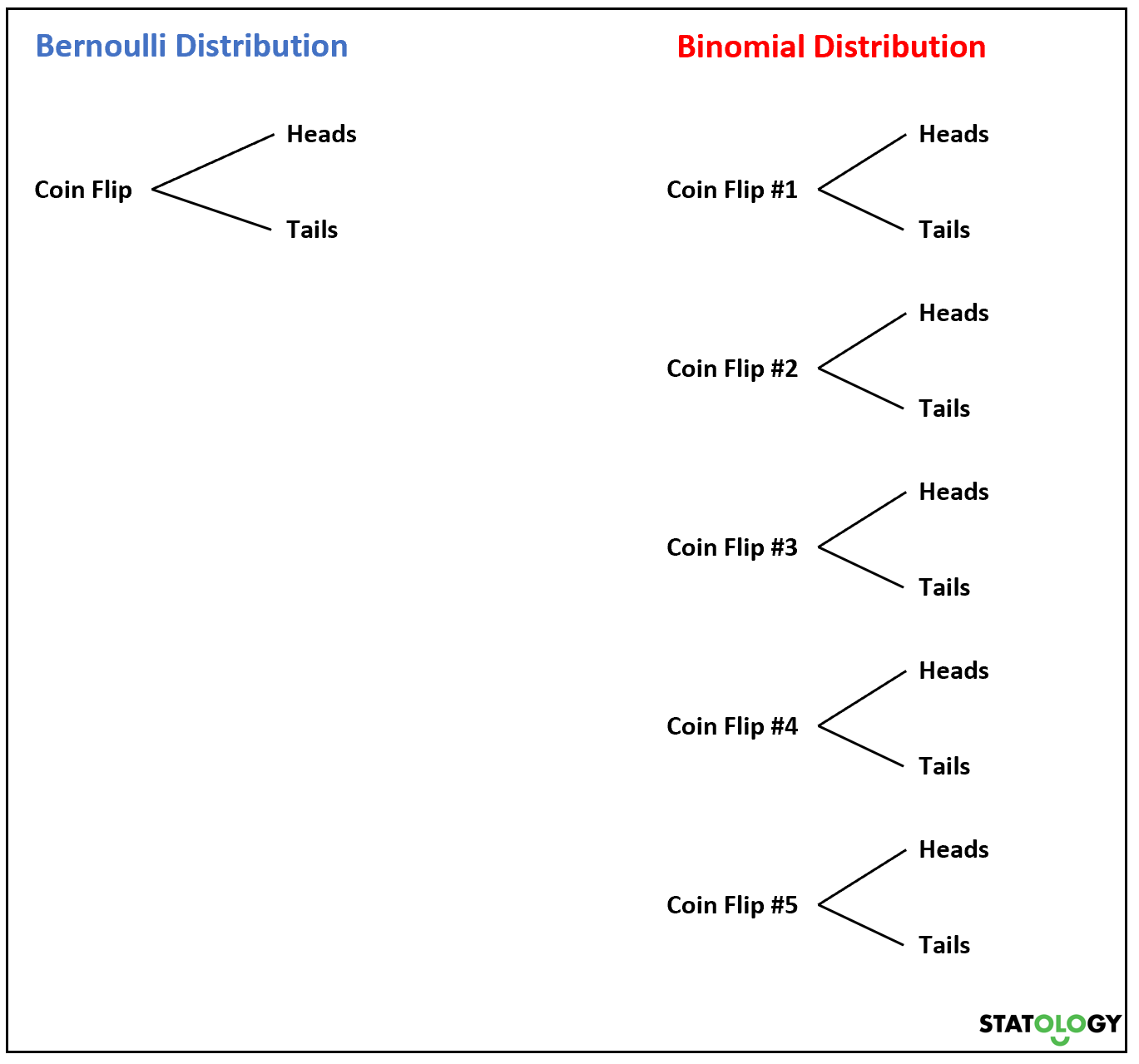
إذا كان المتغير العشوائي X يتبع التوزيع ذي الحدين، فيمكن العثور على احتمال نجاح X = k من خلال الصيغة التالية:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ذهب:

• ن: عدد التجارب
• ك: عدد النجاحات
• ع: احتمال النجاح في تجربة معينة
• _n C _k : عدد الطرق للحصول على نجاحات k في التجارب n

على سبيل المثال، لنفترض أننا نقلب عملة معدنية 3 مرات. يمكننا استخدام الصيغة أعلاه لتحديد احتمالية الحصول على 0 صورة خلال هذه التقلبات الثلاث:

ف(X=0) = ₃ ج ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125

عندما تكون تجربة n = 1، يكون التوزيع ذو الحدين مكافئًا لتوزيع برنولي.

ملاحظات هامة

فيما يلي بعض الملاحظات المهمة بخصوص توزيع برنولي وتوزيع ذي الحدين:

1. المتغير العشوائي الذي يتبع توزيع برنولي يمكن أن يأخذ قيمتين محتملتين فقط، لكن المتغير العشوائي الذي يتبع توزيع ذو الحدين يمكن أن يأخذ عدة قيم.

على سبيل المثال، في رمية عملة واحدة، سيكون لدينا إما 0 أو 1 صورة. ومع ذلك، في سلسلة من 5 سحوبات يمكن أن يكون لدينا 0، 1، 2، 3، 4 أو 5 رؤوس.

2. لكي يتبع المتغير العشوائي التوزيع ذي الحدين، يجب أن يكون احتمال “النجاح” في كل تجربة برنولي متساويًا ومستقلاً.

على سبيل المثال، إذا عرفنا “النجاح” بأنه الهبوط على الرأس، فإن احتمال النجاح في كل رمية هو 0.5 وكل رمية مستقلة – نتيجة الرمية لا تؤثر على نتيجة الرمية الأخرى.

مصادر إضافية

مقدمة للتجارب ذات الحدين
مقدمة للتوزيع ذي الحدين
فهم شكل التوزيع ذي الحدين