ما هي البقايا في الإحصاء؟

والباقي هو الفرق بين القيمة المرصودة والقيمة المتوقعة في تحليل الانحدار .

يتم حسابه على النحو التالي:

المتبقية = القيمة المرصودة – القيمة المتوقعة

تذكر أن الهدف من الانحدار الخطي هو قياس العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة . للقيام بذلك، يبحث الانحدار الخطي عن الخط الذي “يناسب” البيانات بشكل أفضل، ويسمى خط انحدار المربعات الصغرى .

ينتج هذا الخط تنبؤًا لكل ملاحظة في مجموعة البيانات، ولكن من غير المرجح أن يتطابق التنبؤ الذي أجراه خط الانحدار تمامًا مع القيمة المرصودة.

الفرق بين التنبؤ والقيمة المرصودة هو المتبقي. إذا قمنا برسم القيم المرصودة وقمنا بتركيب خط الانحدار المجهز، فإن المتبقي لكل ملاحظة هو المسافة العمودية بين الملاحظة وخط الانحدار:

تحتوي الملاحظة على بقايا إيجابية إذا كانت قيمتها أكبر من القيمة المتوقعة بواسطة خط الانحدار.

وعلى العكس من ذلك، فإن الملاحظة لها بقايا سلبية إذا كانت قيمتها أقل من القيمة المتوقعة بواسطة خط الانحدار.

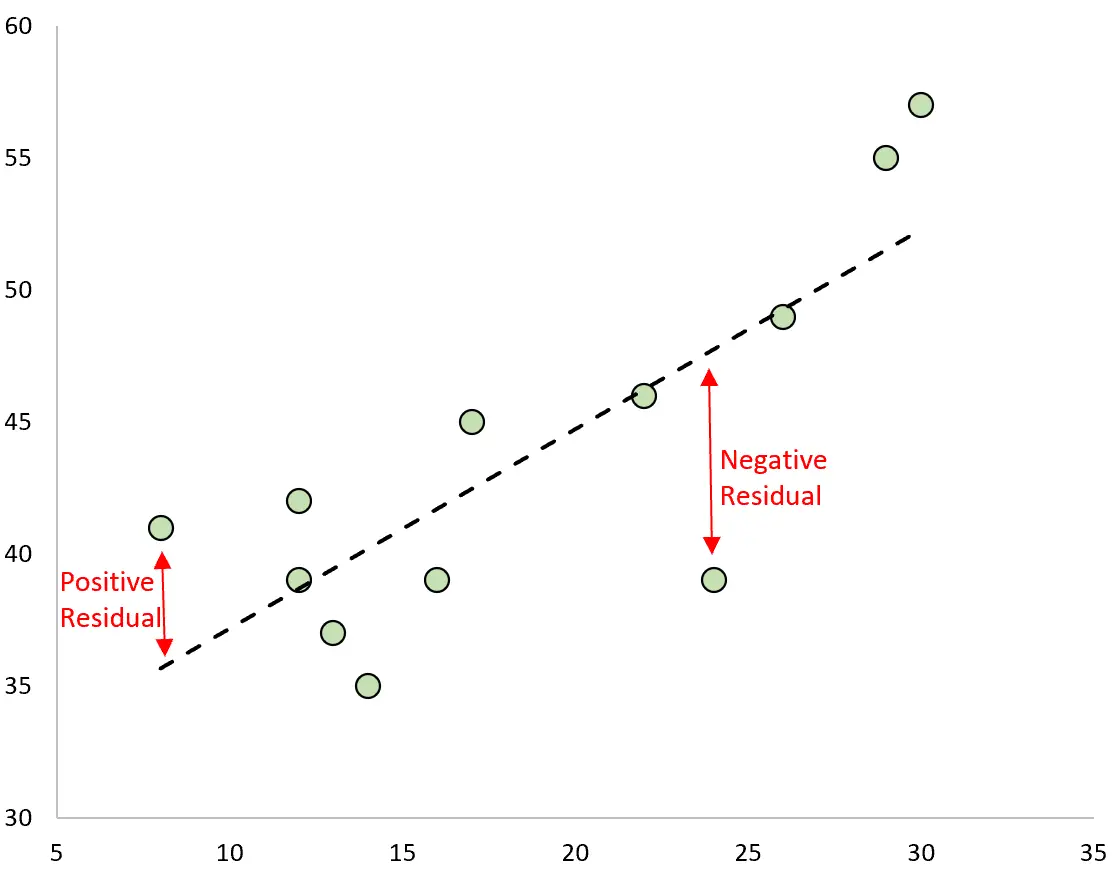
سيكون لبعض الملاحظات بقايا إيجابية في حين أن البعض الآخر سيكون له بقايا سلبية، ولكن جميع المتبقيات سوف يصل مجموعها إلى الصفر .

مثال لحساب البقايا

لنفترض أن لدينا مجموعة البيانات التالية مع إجمالي 12 ملاحظة:

إذا استخدمنا برامج إحصائية (مثل R و Excel و Python و Stata وما إلى ذلك) لملاءمة خط الانحدار الخطي لمجموعة البيانات هذه، فسنجد أن الخط الأكثر ملائمة هو:

ص = 29.63 + 0.7553x

باستخدام هذا الخط، يمكننا حساب القيمة المتوقعة لكل قيمة Y بناءً على قيمة X. على سبيل المثال، القيمة المتوقعة للملاحظة الأولى ستكون:

ص = 29.63 + 0.7553*(8) = 35.67

يمكننا بعد ذلك حساب المتبقي لهذه الملاحظة على النحو التالي:

المتبقية = القيمة المرصودة – القيمة المتوقعة = 41 – 35.67 = 5.33

يمكننا تكرار هذه العملية للعثور على المتبقي لكل ملاحظة:

إذا قمنا بإنشاء مخطط مبعثر لتصور الملاحظات باستخدام خط الانحدار المناسب، فسنرى أن بعض الملاحظات تقع فوق الخط بينما تقع أخرى أسفل الخط:

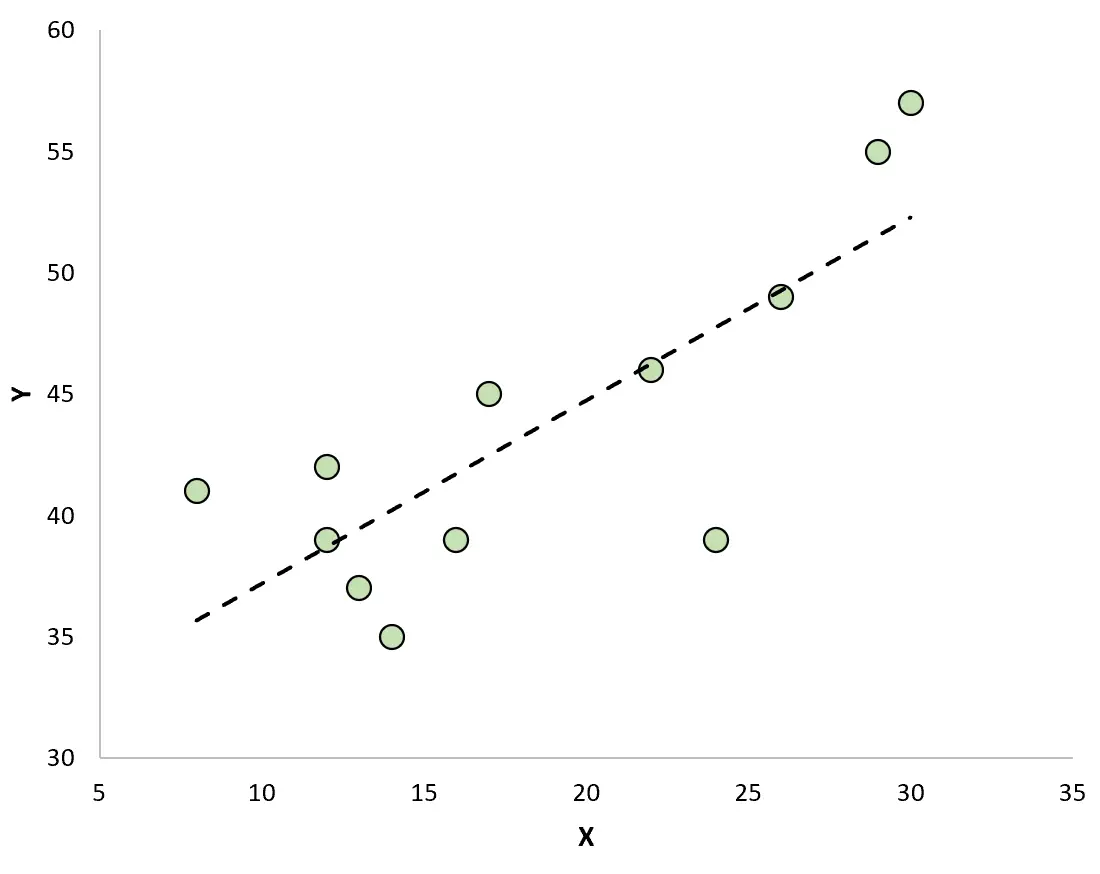
خصائص المخلفات

البقايا لها الخصائص التالية:

• كل ملاحظة في مجموعة البيانات لها ما يقابلها من بقايا. لذلك، إذا كانت مجموعة البيانات تحتوي على 100 ملاحظة في المجموع، فسينتج النموذج 100 قيمة متوقعة، مما يؤدي إلى 100 قيمة متبقية في المجموع.
• مجموع كل المتبقي هو صفر.
• متوسط قيمة المتبقي هو صفر.

كيف يتم استخدام المخلفات في الممارسة العملية؟

من الناحية العملية، يتم استخدام القيم المتبقية لثلاثة أسباب مختلفة في الانحدار:

1. تقييم مدى كفاية النموذج.

بمجرد إنتاج خط الانحدار المناسب، يمكننا حساب مجموع المربعات المتبقية (RSS) ، وهو مجموع جميع المربعات المتبقية. كلما انخفض RSS، كان نموذج الانحدار مناسبًا للبيانات بشكل أفضل.

2. التحقق من افتراض الحالة الطبيعية.

أحد الافتراضات الرئيسية للانحدار الخطي هو أن البقايا يتم توزيعها بشكل طبيعي.

لاختبار هذه الفرضية، يمكننا إنشاء مخطط QQ، وهو نوع من المخططات التي يمكننا استخدامها لتحديد ما إذا كانت بقايا النموذج تتبع التوزيع الطبيعي أم لا.

إذا كانت النقاط الموجودة على قطعة الأرض تشكل خطًا قطريًا مستقيمًا تقريبًا، فإن افتراض الحالة الطبيعية قد تحقق.

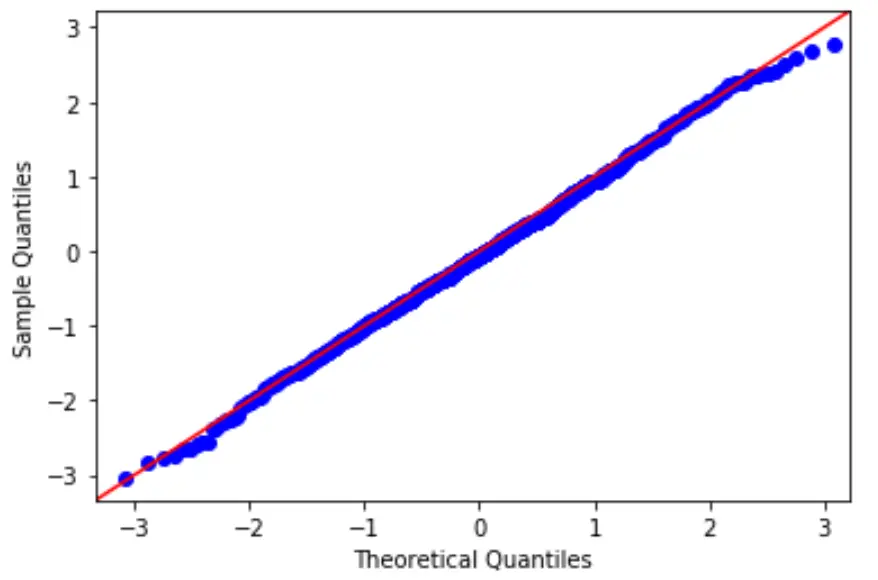
3. التحقق من افتراض المثلية.

الافتراض الرئيسي الآخر للانحدار الخطي هو أن البقايا لها تباين ثابت عند كل مستوى من x. وهذا ما يسمى المثلية. عندما لا يكون الأمر كذلك، فإن البقايا تعاني من عدم تجانسها .

للتحقق من استيفاء هذا الافتراض، يمكننا إنشاء مخطط المخلفات ، وهو مخطط التشتت الذي يوضح البقايا مقابل القيم المتوقعة للنموذج.

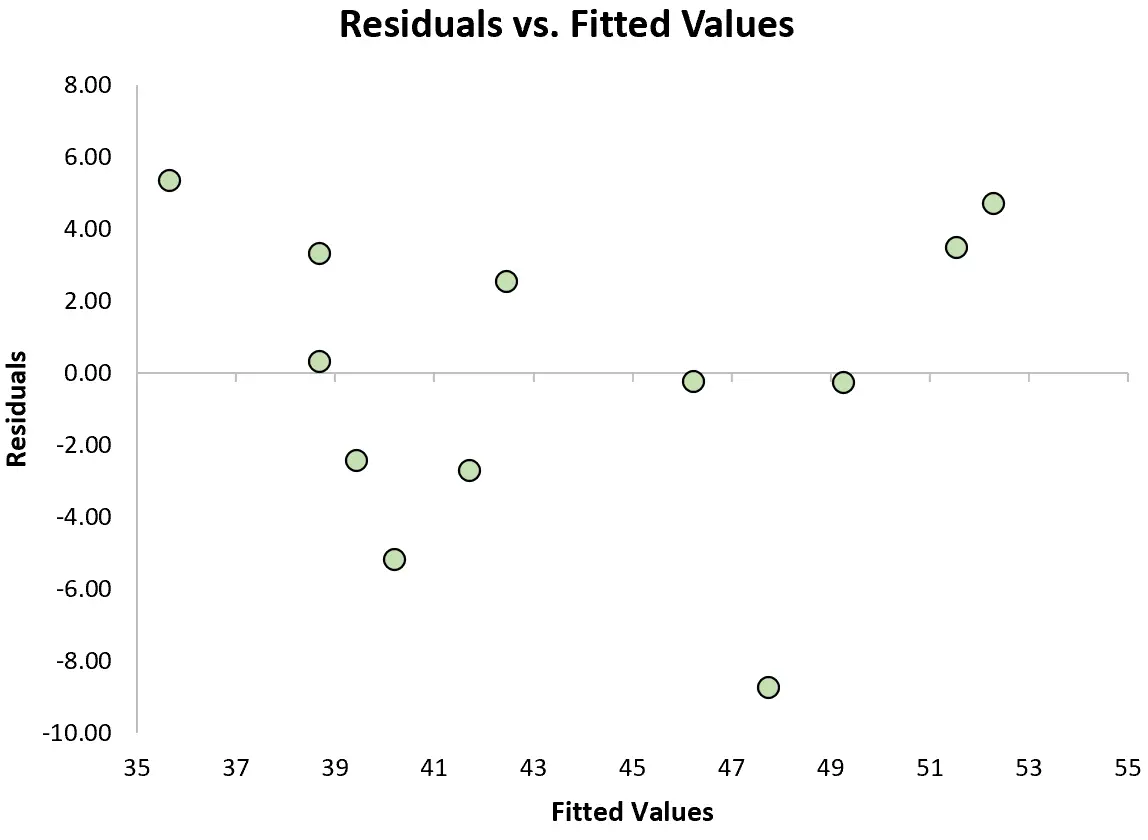
إذا تم توزيع البقايا بالتساوي تقريبًا حول الصفر في الرسم البياني مع عدم وجود اتجاه واضح، فإننا نقول بشكل عام أن افتراض التجانس قد تم استيفائه.

مصادر إضافية

مقدمة إلى الانحدار الخطي البسيط
مقدمة في الانحدار الخطي المتعدد
الافتراضات الأربعة للانحدار الخطي
كيفية إنشاء مؤامرة المتبقية في إكسيل