كيفية تحليل المخلفات في نموذج anova
ANOVA (“تحليل التباين”) هو نوع من النماذج المستخدمة لتحديد ما إذا كان هناك فرق كبير بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.
نحن نلائم تحليل التباين (ANOVA) كلما كان النموذج متوافقًا مع مجموعة بيانات، سيكون هناك دائمًا بقايا – تمثل الفرق بين كل ملاحظة فردية ومتوسط المجموعة التي جاءت منها الملاحظة.
يوضح المثال التالي كيفية حساب القيم المتبقية لنموذج ANOVA عمليًا.
مثال: حساب المخلفات في تحليل التباين (ANOVA).
لنفترض أننا قمنا بتجنيد 90 شخصًا للمشاركة في تجربة لإنقاص الوزن حيث قمنا بتعيين 30 شخصًا بشكل عشوائي لمتابعة البرنامج أ أو البرنامج ب أو البرنامج ج لمدة شهر.
يمكننا إجراء تحليل التباين (ANOVA) أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين فقدان الوزن الناتج عن البرامج الثلاثة.
لنفترض أننا قمنا بحساب متوسط فقدان الوزن للأفراد المشاركين في كل برنامج على النحو التالي:
- البرنامج أ : 1.58 جنيه
- البرنامج ب : 2.56 جنيه
- البرنامج ج : 4.13 جنيه
ستكون البقايا من نموذج ANOVA هي الفرق بين فقدان الوزن لكل فرد ومتوسط فقدان الوزن لبرنامجه.
على سبيل المثال، يوضح الجدول التالي كيفية حساب البقايا لـ 10 أفراد مختلفين في الدراسة:
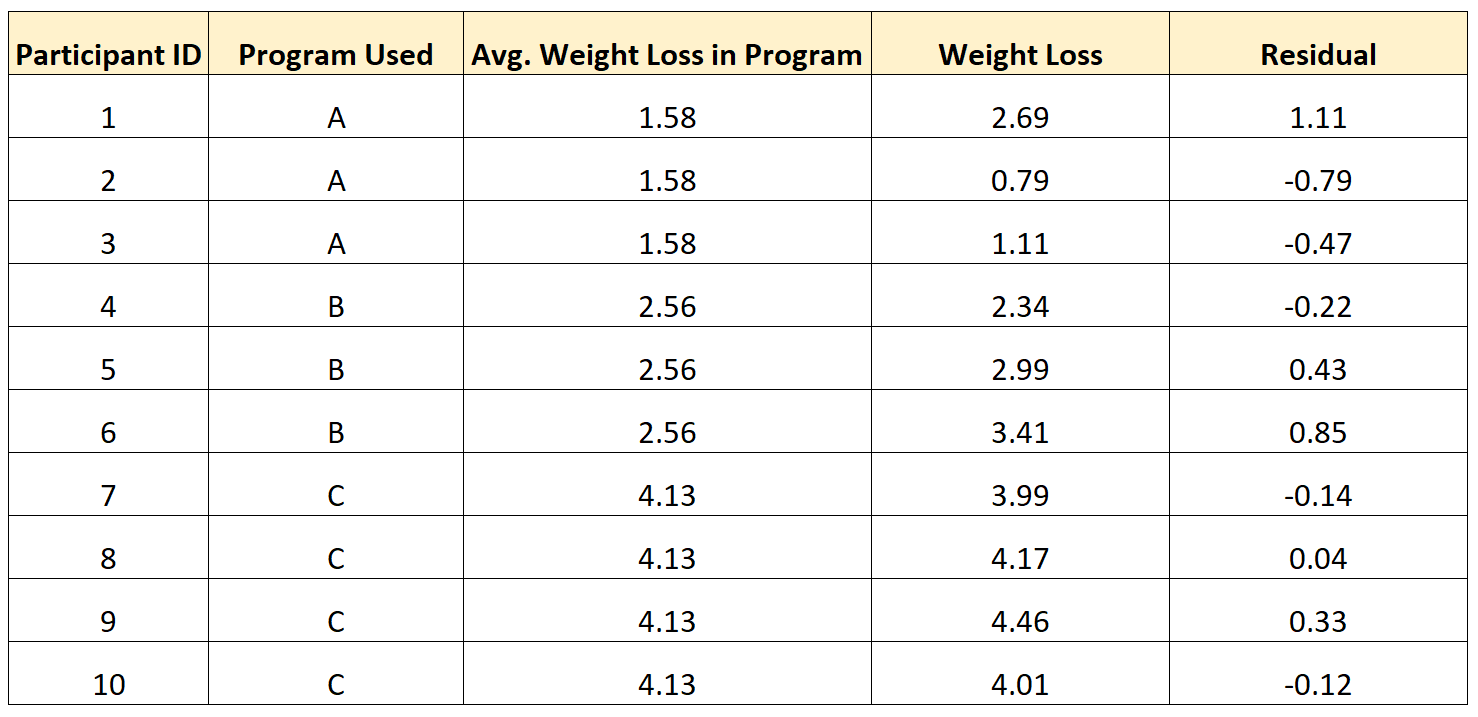
لاحظ النمط التالي:
- الأفراد الذين كانت لديهم قيمة أعلى من متوسط مجموعتهم كان لديهم بقايا إيجابية .
- الأفراد الذين لديهم قيمة أقل من متوسط مجموعتهم كان لديهم بقايا سلبية .
ومن الناحية العملية، يمكننا حساب المتبقي لجميع الأفراد التسعين.
كيفية استخدام المخلفات للتحقق من الحالة الطبيعية
أحد افتراضات ANOVA هو أن البقايا يتم توزيعها بشكل طبيعي.
الطريقة الأكثر شيوعًا للتحقق من هذا الافتراض هي إنشاء مخطط QQ .
إذا تم توزيع البقايا بشكل طبيعي، فستقع النقاط الموجودة على مخطط QQ على خط قطري مستقيم.
إليك ما ستبدو عليه مخطط QQ في مثالنا السابق:
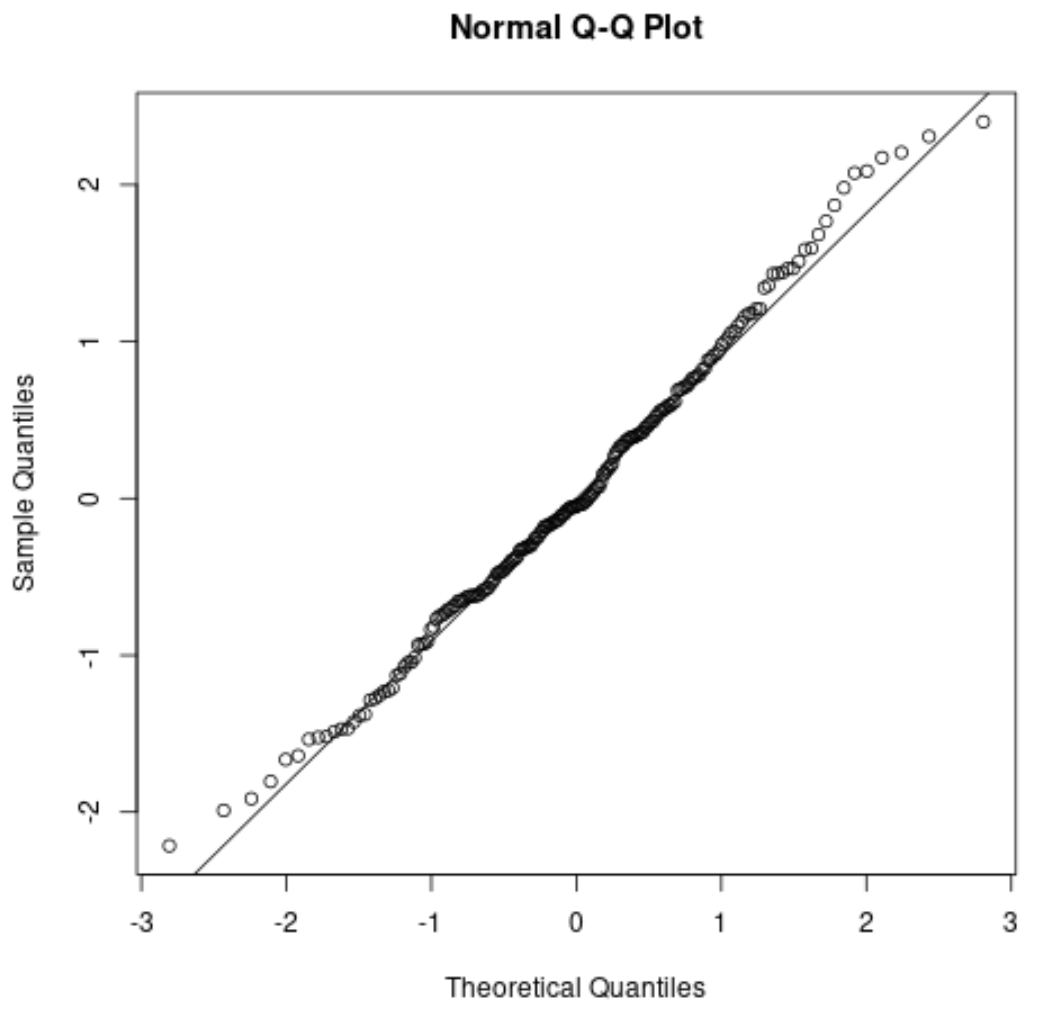
تنحرف الأطراف قليلاً عن الخط القطري المستقيم في نهايات الذيل، لكن بشكل عام تتبع الأطراف الخط القطري بشكل جيد. وهذا يخبرنا أنه من المحتمل أن يتم استيفاء افتراض الحالة الطبيعية.
كمرجع، إليك ما قد يبدو عليه مخطط QQ للمخلفات غير الموزعة بشكل طبيعي:
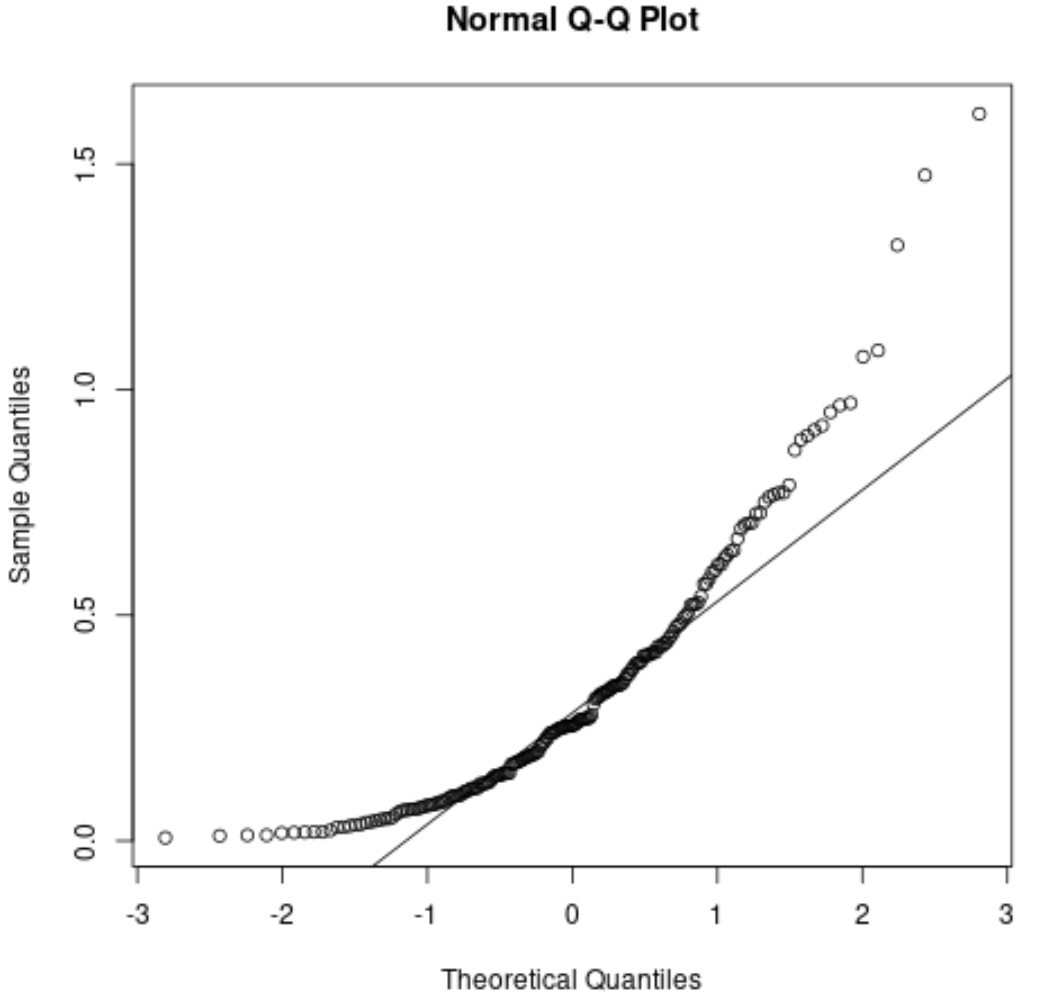
تنحرف النقاط بشكل كبير عن الخط القطري المستقيم، مما يشير إلى أن البقايا لا يتم توزيعها بشكل طبيعي.
ارجع إلى البرامج التعليمية التالية لمعرفة كيفية إنشاء مخططات QQ في برامج مختلفة:
مصادر إضافية
توفر المقالات التالية معلومات إضافية حول نماذج ANOVA:
مقدمة إلى تحليل التباين الأحادي (One-Way ANOVA).
كيفية التحقق من افتراضات ANOVA
4 أمثلة لاستخدام ANOVA في الحياة الواقعية
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر