ما هي المخلفات الموحدة؟

المتبقي هو الفرق بين القيمة المرصودة والقيمة المتوقعة في نموذج الانحدار .

يتم حسابه على النحو التالي:

المتبقية = القيمة المرصودة – القيمة المتوقعة

إذا قمنا برسم القيم المرصودة وقمنا بتركيب خط الانحدار المجهز، فإن المتبقي لكل ملاحظة هو المسافة العمودية بين الملاحظة وخط الانحدار:

أحد الأنواع المتبقية التي نستخدمها غالبًا لتحديد القيم المتطرفة في نموذج الانحدار يسمى المتبقي القياسي .

يتم حسابه على النحو التالي:

r _i = e _i / s(e _i ) = e _i / RSE√ 1-h _ii

ذهب:

• e _i : ^{البقايا} i
• RSE: الخطأ المعياري المتبقي للنموذج
• الح _{الثانية} : طلوع الملاحظة ^{الثامنة}

من الناحية العملية، غالبًا ما نعتبر أي قيمة متبقية موحدة تكون قيمتها المطلقة أكبر من 3 بمثابة قيمة متطرفة.

وهذا لا يعني بالضرورة أننا سوف نقوم بإزالة هذه الملاحظات من النموذج، ولكن يجب علينا على الأقل دراستها بشكل أكبر للتأكد من أنها ليست نتيجة خطأ في إدخال البيانات أو أي حدث غريب آخر.

ملحوظة: في بعض الأحيان تسمى المخلفات المعيارية أيضًا “المخلفات المدروسة داخليًا”.

مثال: كيفية حساب المخلفات الموحدة

لنفترض أن لدينا مجموعة البيانات التالية مع إجمالي 12 ملاحظة:

إذا استخدمنا برامج إحصائية (مثل R و Excel و Python و Stata وما إلى ذلك) لملاءمة خط الانحدار الخطي لمجموعة البيانات هذه، فسنجد أن الخط الأكثر ملائمة هو:

ص = 29.63 + 0.7553x

باستخدام هذا الخط، يمكننا حساب القيمة المتوقعة لكل قيمة Y بناءً على قيمة X. على سبيل المثال، القيمة المتوقعة للملاحظة الأولى ستكون:

ص = 29.63 + 0.7553*(8) = 35.67

يمكننا بعد ذلك حساب المتبقي لهذه الملاحظة على النحو التالي:

المتبقية = القيمة المرصودة – القيمة المتوقعة = 41 – 35.67 = 5.33

يمكننا تكرار هذه العملية للعثور على المتبقي لكل ملاحظة:

يمكننا أيضًا استخدام البرامج الإحصائية لنجد أن الخطأ المعياري المتبقي للنموذج هو 4.44 .

وعلى الرغم من أن ذلك خارج نطاق هذا البرنامج التعليمي، يمكننا استخدام البرنامج للعثور على إحصائية الرافعة المالية (h _ii ) لكل ملاحظة:

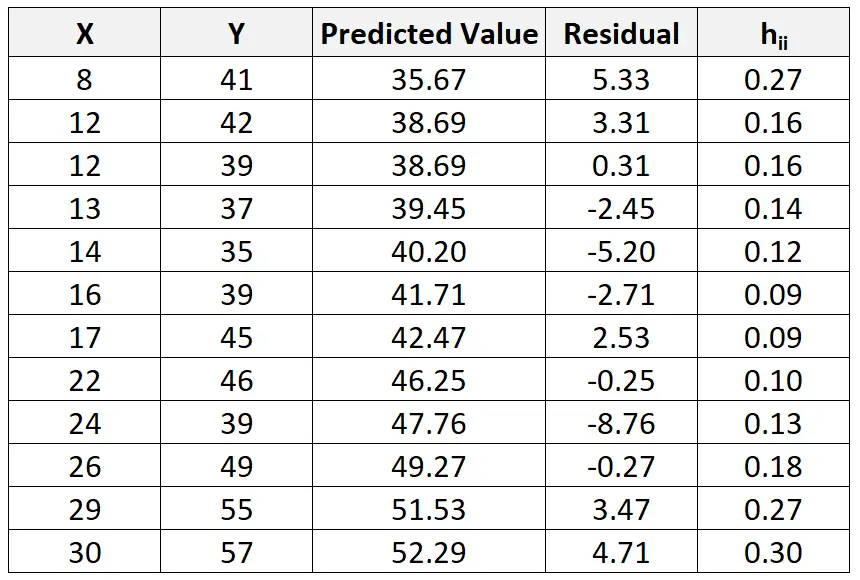
يمكننا بعد ذلك استخدام الصيغة التالية لحساب المتبقي القياسي لكل ملاحظة:

ص _أنا = ه _أنا / RSE√ 1-ح _ثانيا

على سبيل المثال، يتم حساب المتبقي الموحد للملاحظة الأولى على النحو التالي:

ص _ط = 5.33 / 4.44√ 1-0.27 = 1.404

يمكننا تكرار هذه العملية للعثور على المتبقي القياسي لكل ملاحظة:

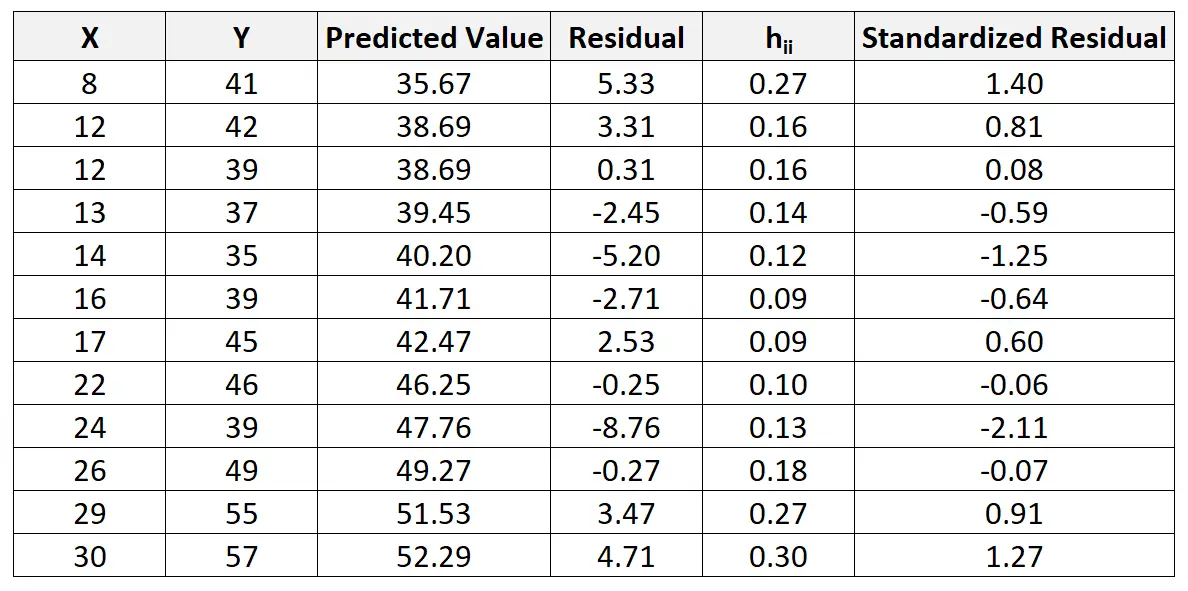
يمكننا بعد ذلك إنشاء مخطط تشتت سريع للقيم التنبؤية مقابل المخلفات القياسية لنرى بصريًا ما إذا كان أي من المخلفات القياسية يتجاوز عتبة القيمة المطلقة البالغة 3:

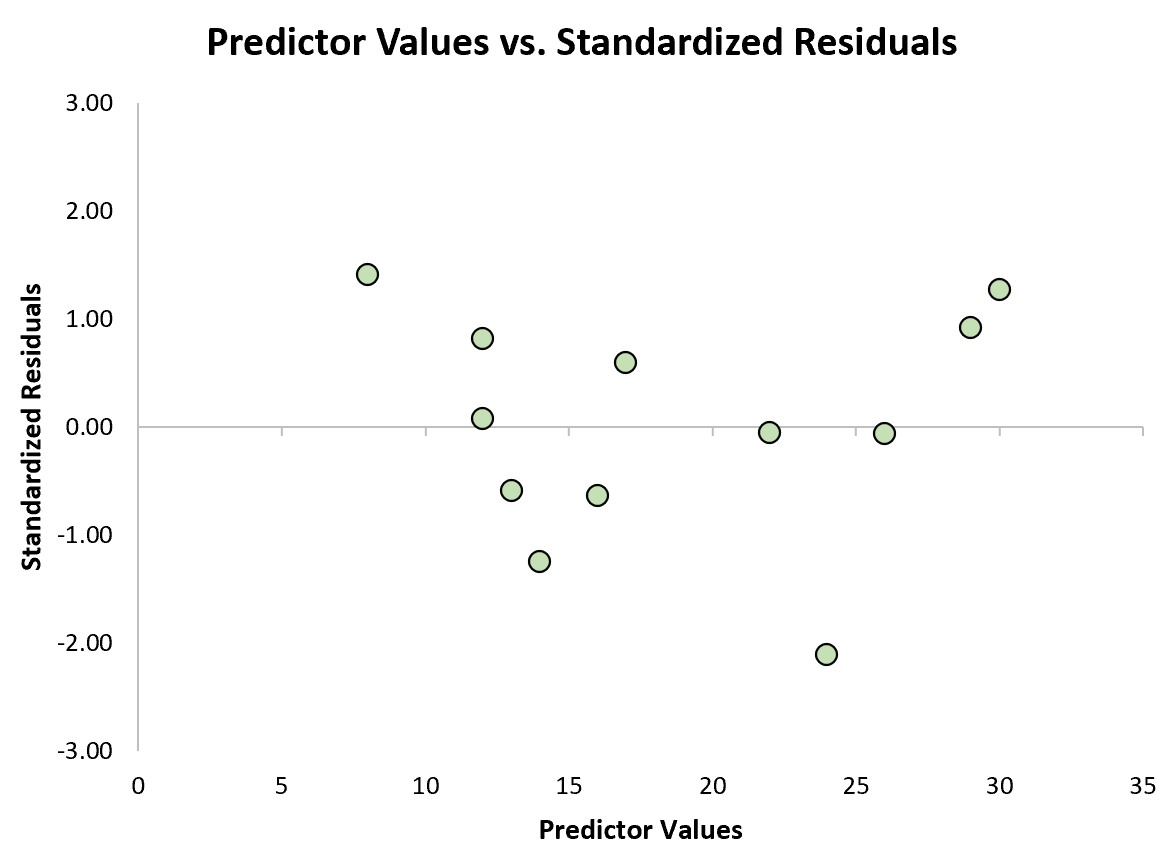
من الرسم البياني، يمكننا أن نرى أن أيًا من القيم المتبقية القياسية لا يتجاوز القيمة المطلقة البالغة 3. وبالتالي، لا يبدو أن أيًا من الملاحظات تعتبر قيمًا متطرفة.

تجدر الإشارة إلى أنه في بعض الحالات، يعتبر الباحثون الملاحظات التي تتجاوز القيم المتبقية المعيارية القيمة المطلقة 2 بمثابة قيم متطرفة.

الأمر متروك لك، اعتمادًا على المجال الذي تعمل فيه والمشكلة المحددة التي تعمل عليها، سواء كنت تريد استخدام قيمة مطلقة تبلغ 2 أو 3 كحد أقصى للقيم المتطرفة.

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول المخلفات القياسية:

ما هي البقايا في الإحصاء؟
كيفية حساب المخلفات الموحدة في إكسيل
كيفية حساب المخلفات الموحدة في R
كيفية حساب المخلفات الموحدة في بيثون