كيفية استخدام التوزيع ذي الحدين في بايثون

التوزيع ذو الحدين هو أحد التوزيعات الأكثر استخدامًا في الإحصاء. فهو يصف احتمالية الحصول على نجاحات k في تجارب ذات الحدين n .

إذا كان المتغير العشوائي X يتبع التوزيع ذي الحدين، فيمكن العثور على احتمال نجاح X = k من خلال الصيغة التالية:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ذهب:

• ن: عدد التجارب
• ك: عدد النجاحات
• ع: احتمال النجاح في تجربة معينة
• _n C _k : عدد الطرق للحصول على نجاحات k في التجارب n

يشرح هذا البرنامج التعليمي كيفية استخدام التوزيع ذي الحدين في بايثون.

كيفية توليد توزيع ذي الحدين

يمكنك إنشاء مصفوفة من القيم التي تتبع توزيعًا ذا الحدين باستخدام الدالة Random.Binomial الخاصة بالمكتبة numpy:

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

يمثل كل رقم في الجدول الناتج عدد “النجاحات” التي تمت مواجهتها على مدار 10 تجارب حيث كان احتمال النجاح في تجربة معينة 0.25 .

كيفية حساب الاحتمالات باستخدام التوزيع ذي الحدين

يمكنك أيضًا الإجابة على أسئلة حول الاحتمالية ذات الحدين باستخدام دالة binom الخاصة بمكتبة scipy.

السؤال 1: قام ناثان بنسبة 60% من محاولات الرمية الحرة. إذا نفذ 12 رمية حرة، فما احتمال أن ينفذ 10 رميات بالضبط؟

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

احتمال قيام ناثان بتنفيذ 10 رميات حرة بالضبط هو 0.0639 .

السؤال الثاني: يقلب مارتي قطعة نقدية نظيفة 5 مرات. ما هو احتمال ظهور العملة على الوجه مرتين أو أقل؟

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

احتمال ظهور العملة على الوجه مرتين أو أقل هو 0.5 .

السؤال الثالث: نعلم أن 70% من الأفراد يؤيدون قانونًا معينًا. إذا تم اختيار 10 أفراد عشوائيًا، فما احتمال أن يؤيد ما بين 4 إلى 6 منهم القانون؟

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

احتمال أن يدعم القانون ما بين 4 إلى 6 أفراد تم اختيارهم عشوائيًا هو 0.3398 .

كيفية تصور التوزيع ذي الحدين

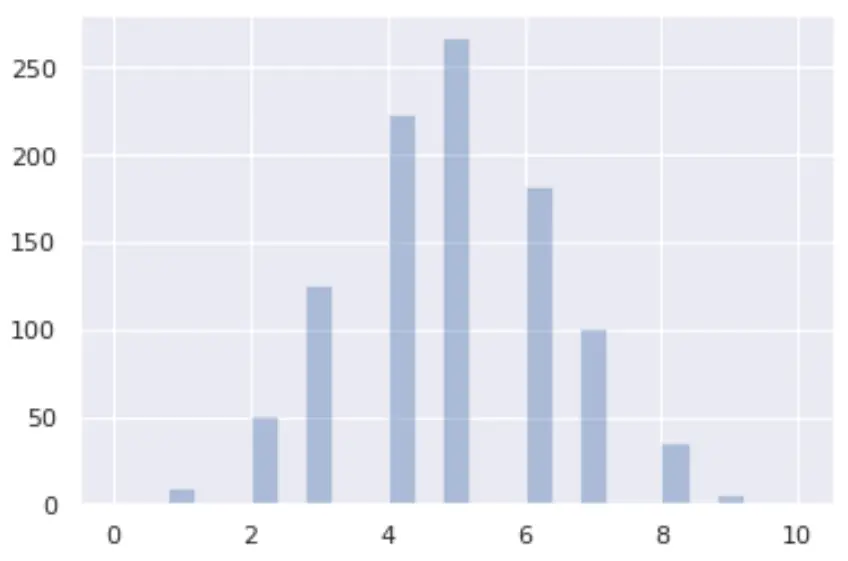
يمكنك تصور التوزيع ذي الحدين في بايثون باستخدام مكتبات seaborn و matplotlib :

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

شاي