كيفية حساب التباين في التوزيع الاحتمالي

يخبرنا التوزيع الاحتمالي باحتمال أن يأخذ المتغير العشوائي قيمًا معينة.

على سبيل المثال، يخبرنا التوزيع الاحتمالي التالي باحتمالية أن يسجل فريق كرة قدم معين عددًا معينًا من الأهداف في مباراة معينة:

لإيجاد تباين التوزيع الاحتمالي يمكننا استخدام الصيغة التالية:

σ ² = Σ(x _i -μ) ² * P(x _i )

ذهب:

• _xi : القيمة ^رقم
• μ: متوسط التوزيع
• P(x _i ): احتمال القيمة ⁱ

على سبيل المثال، فكر في التوزيع الاحتمالي لفريق كرة القدم:

سيتم حساب متوسط عدد الأهداف التي يسجلها فريق كرة القدم على النحو التالي:

μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45 هدف.

يمكننا بعد ذلك حساب التباين على النحو التالي:

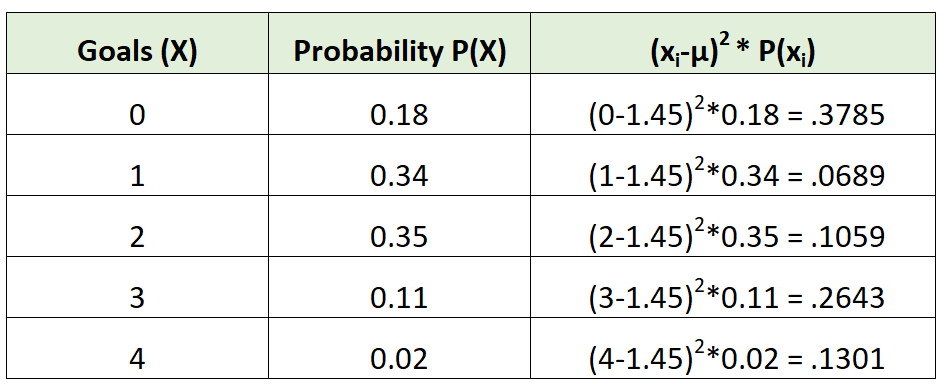
التباين هو ببساطة مجموع القيم في العمود الثالث. لذلك سنحسبها كالآتي:

^σ2 = 0.3785 + 0.0689 + 0.1059 + 0.2643 + 0.1301 = 0.9475

توضح الأمثلة التالية كيفية حساب تباين التوزيع الاحتمالي في بعض السيناريوهات الأخرى.

مثال 1: التباين في أعطال المركبات

يخبرنا توزيع الاحتمالات التالي باحتمالية تعرض مركبة معينة لعدد معين من حالات فشل البطارية خلال فترة 10 سنوات:

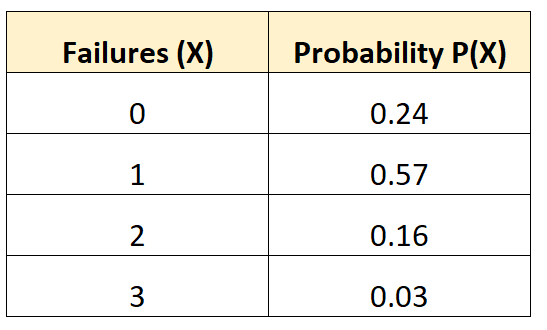
للعثور على تباين هذا التوزيع الاحتمالي، نحتاج أولاً إلى حساب متوسط عدد حالات الفشل المتوقعة:

μ = 0*0.24 + 1*0.57 + 2*0.16 + 3*0.03 = 0.98 حالات فشل.

يمكننا بعد ذلك حساب التباين على النحو التالي:

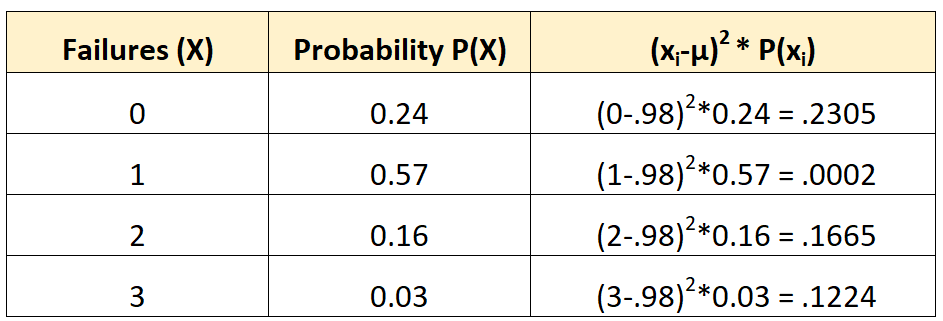
التباين هو مجموع القيم في العمود الثالث. لذلك سنحسبها كالآتي:

^σ2 = 0.2305 + 0.0002 + 0.1665 + 0.1224 = 0.5196

مثال 2: تباين المبيعات

يخبرنا التوزيع الاحتمالي التالي باحتمال قيام بائع معين بإجراء عدد معين من المبيعات في الشهر القادم:

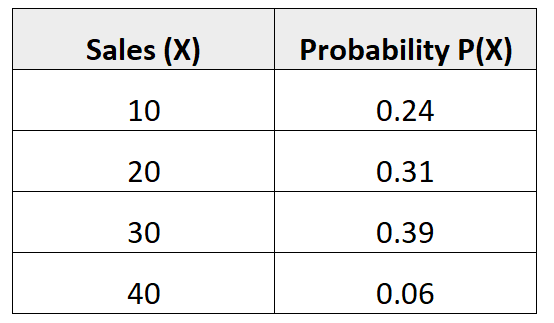
للعثور على تباين هذا التوزيع الاحتمالي، نحتاج أولاً إلى حساب متوسط عدد المبيعات المتوقعة:

μ = 10*0.24 + 20*0.31 + 30*0.39 + 40*0.06 = 22.7 قذرة.

يمكننا بعد ذلك حساب التباين على النحو التالي:

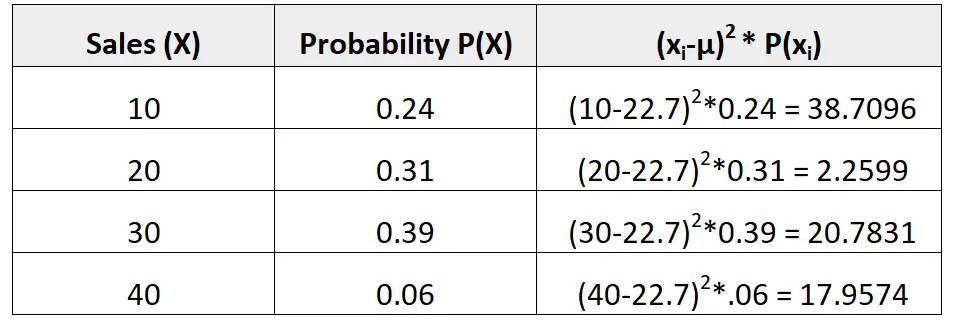
التباين هو مجموع القيم في العمود الثالث. لذلك سنحسبها كالآتي:

^σ2 = 38.7096 + 2.2599 + 20.7831 + 17.9574 = 79.71

لاحظ أنه يمكننا أيضًا استخدام حاسبة التوزيع الاحتمالي لحساب تباين هذا التوزيع تلقائيًا:

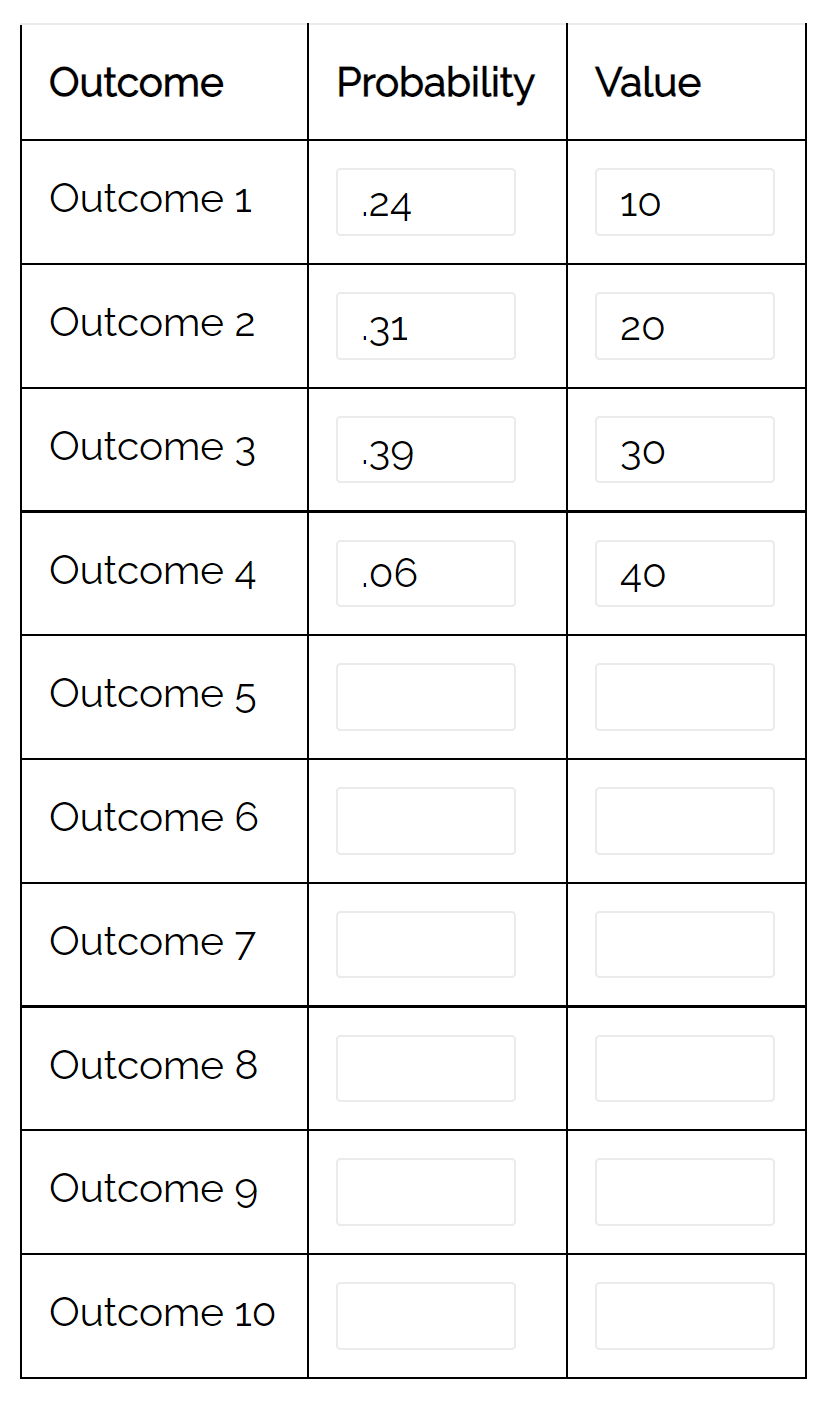
الفارق 79.71 . وهذا يتوافق مع القيمة التي حسبناها يدويًا.