كيفية تطبيق نظرية تشيبيشيف في إكسل
تنص نظرية تشيبيشيف على أنه بالنسبة لأي رقم k أكبر من 1، فإن 1 – 1/k 2 على الأقل من قيم البيانات في أي توزيع مدرب تقع ضمن انحرافات معيارية k عن المتوسط.
على سبيل المثال، بالنسبة لأي توزيع على شكل، على الأقل 1 – 1/3 2 = 88.89% من القيم في التوزيع سوف تقع ضمن 3 انحرافات معيارية للمتوسط.
يوضح هذا البرنامج التعليمي عدة أمثلة لتطبيق نظرية Chebyshev في Excel.
مثال 1: استخدم نظرية تشيبيشيف لتحديد النسبة المئوية للقيم التي تقع بين 30 و70 لمجموعة بيانات بمتوسط 50 وانحراف معياري 10.
أولا، تحديد قيمة ك. يمكننا القيام بذلك عن طريق تحديد عدد الانحرافات المعيارية التي تتراوح بين 30 و70 من المتوسط:
(30 – المتوسط) / الانحراف المعياري = (30 – 50) / 10 = -20 / 10 = -2
(70 – المتوسط) / الانحراف المعياري = (70 – 50) / 10 = 20 / 10 = 2
القيمتان 30 و70 هما انحرافان معياريان أقل من المتوسط وفوقه، على التوالي. إذن ك = 2 .
يمكننا بعد ذلك استخدام الصيغة التالية في Excel للعثور على الحد الأدنى لنسبة القيم التي تقع ضمن انحرافين معياريين عن المتوسط لمجموعة البيانات هذه:
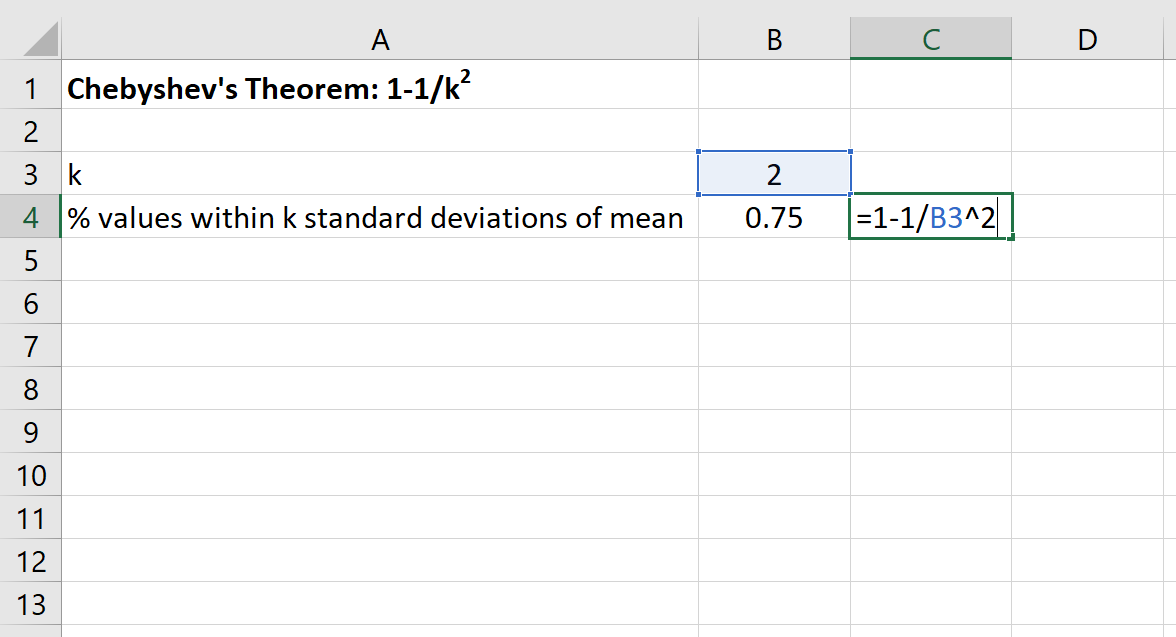
ستكون نسبة القيم بين 30 و 70 لمجموعة البيانات هذه 75% على الأقل .
مثال 2: استخدم نظرية تشيبيشيف لتحديد النسبة المئوية للقيم التي تقع بين 20 و50 لمجموعة بيانات بمتوسط 35 وانحراف معياري 5.
أولا، تحديد قيمة ك. يمكننا القيام بذلك عن طريق تحديد عدد الانحرافات المعيارية التي تتراوح بين 20 و50 من المتوسط:
(20 – المتوسط) / الانحراف المعياري = (20 – 35) / 5 = -15 / 5 = -3
(50 – المتوسط) / الانحراف المعياري = (50 – 35) / 5 = 15 / 5 = 3
القيمتان 20 و 50 عبارة عن 3 انحرافات معيارية أقل وأعلى من المتوسط، على التوالي. إذن ك = 3 .
يمكننا بعد ذلك استخدام الصيغة التالية في Excel للعثور على الحد الأدنى لنسبة القيم التي تقع ضمن 3 انحرافات معيارية للمتوسط لمجموعة البيانات هذه:
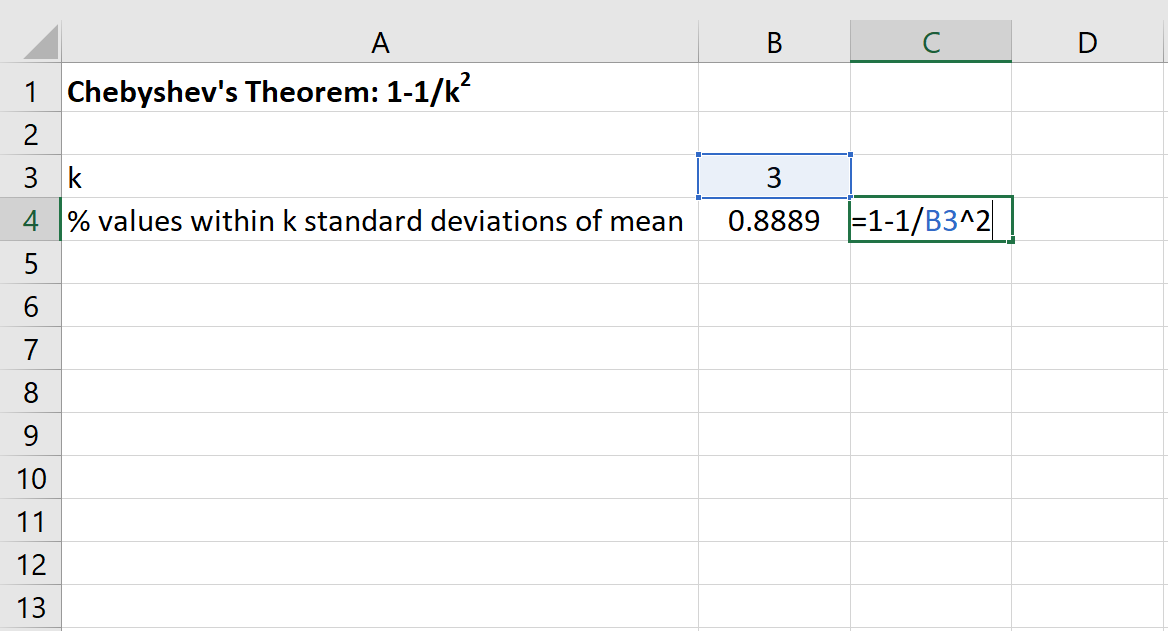
ستكون نسبة القيم بين 20 و50 لمجموعة البيانات هذه 88.89% على الأقل .
مثال 3: استخدم نظرية تشيبيشيف لتحديد النسبة المئوية للقيم التي تقع بين 80 و120 لمجموعة بيانات بمتوسط 100 وانحراف معياري قدره 5.
أولا، تحديد قيمة ك. يمكننا القيام بذلك عن طريق تحديد عدد الانحرافات المعيارية التي تتراوح بين 80 و120 عن المتوسط:
(80 – المتوسط) / الانحراف المعياري = (80 – 100) / 5 = -20 / 5 = -4
(120 – المتوسط) / الانحراف المعياري = (120 – 100) / 5 = 20 / 5 = 4
القيمتان 80 و 120 عبارة عن 4 انحرافات معيارية أقل من المتوسط وفوقه على التوالي. إذن ك = 4 .
يمكننا بعد ذلك استخدام الصيغة التالية في Excel للعثور على الحد الأدنى لنسبة القيم التي تقع ضمن 4 انحرافات معيارية للمتوسط لمجموعة البيانات هذه:
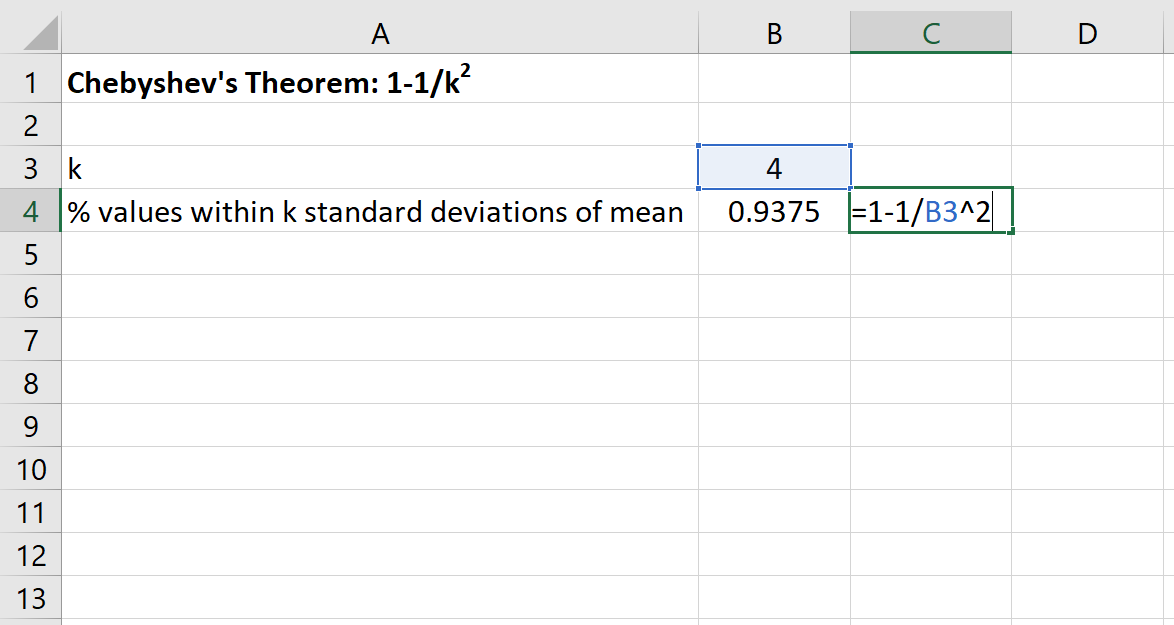
ستكون نسبة القيم بين 80 و 120 لمجموعة البيانات هذه 93.75% على الأقل .